某校现代控制大作业
某校现代控制大作业,流程大概如此,新一届不被折磨
设计要求:**
依据题目所给条件,超调不超过 10%,调整时间不超过 15
秒,算得主导极点阻尼比小于0.589,自然频率0.396,两通道均可采用lqr进行状态反馈器设计。
考虑到固定翼无无人机结构稳定,科学载荷,飞行状态平稳及计算精度影响,控制器设置固定翼无人机加速过载小于2g,即调整时间大于7s,小于15s。
LQR线性二次型调节器:LQR可得到状态线性反馈的最优控制规律,易于构成闭环最优控制。
当系统只拥有纯实根时响应达到无超调,在设定系统极点时,使虚部尽量接近于零,这样的系统就能够快速响应无超调。对于反馈矩阵K的求取,可以直接利用MATLAB自带的K
=lqr(sys,Q,R)函数。
系统1:输入:δT**
状态矩阵:Alo=[-0.018 10.44 -9.797 0.153 -0.0001
-0.0003 -1.083 0 0.938 0.00
0 0 0 1 0
0 0 -2.622 -1.407 0
0 230 -230 0 0]
Blo=[7.0609
0
0
0
0 ]
Clo=[0 1 0 0 0
0 0 1 0 0]
Dlo=[0;0;0;0;0]
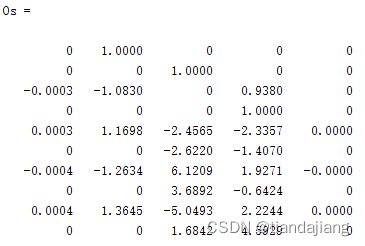
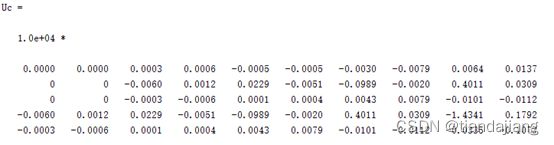
系统能控性分析:
Rank(Uc)=3,可得系统不可控
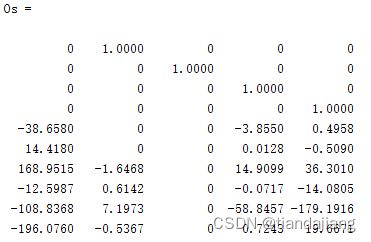
系统能观性分析:
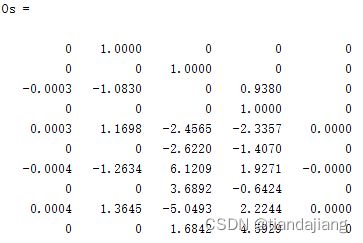
Rank(Os)=5,可得系统可观
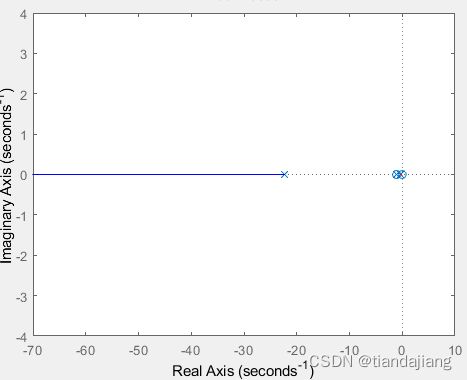
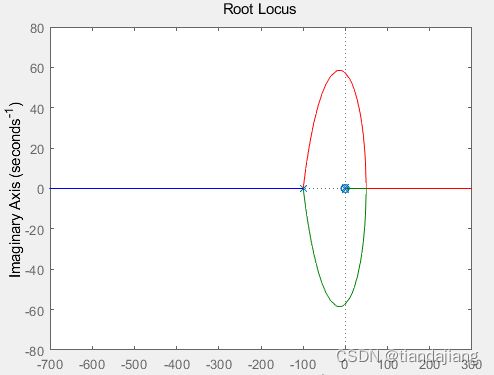
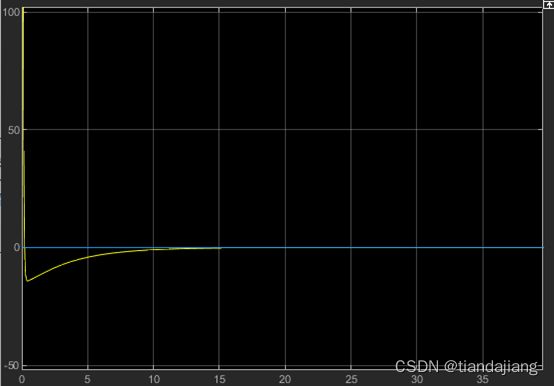
根轨迹如图,可知配置系统稳定且响应无震荡,系统可任意配置极点。
图 1 根轨迹
状态反馈器配置**
系统能观不能控,且由其根轨迹可以得出系统任意配置极点均稳定,使用LQR配置零极点。
为使得超调量小,应使得根靠近实轴。设置R=0.1
权重矩阵 Q=
[1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 20]
配置得到反馈矩阵 K=[3.2 -2700.3 4190 1034.9 -14.1]
配置得到的极点为 P=[-22.3283;-1.0416;-0.2963]
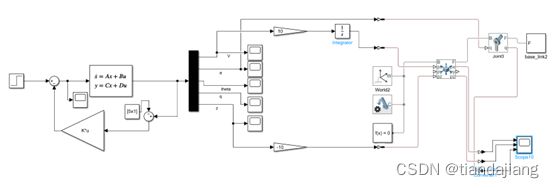
使用simulink搭建仿真模型
图 2 simulink 仿真图
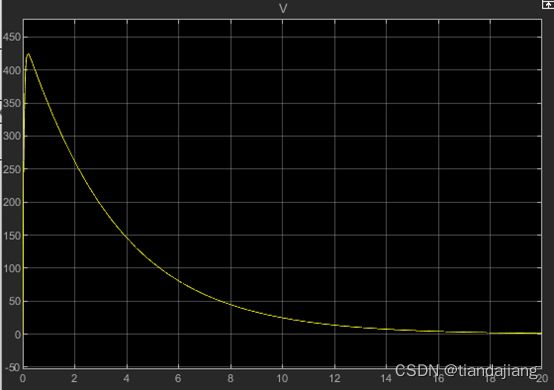
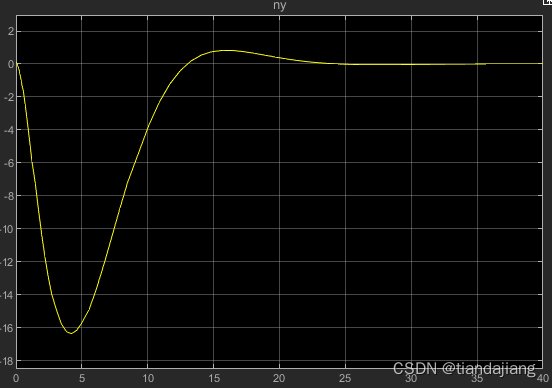
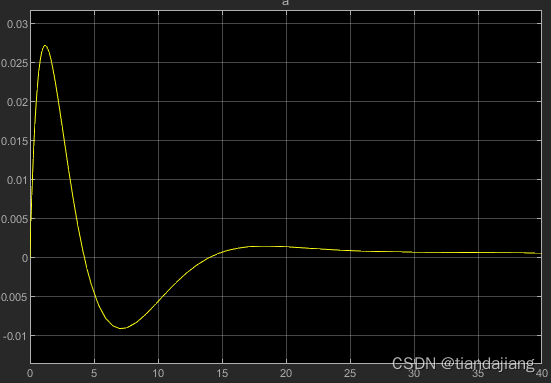
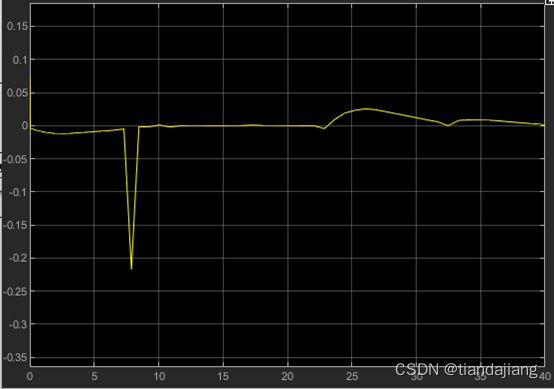
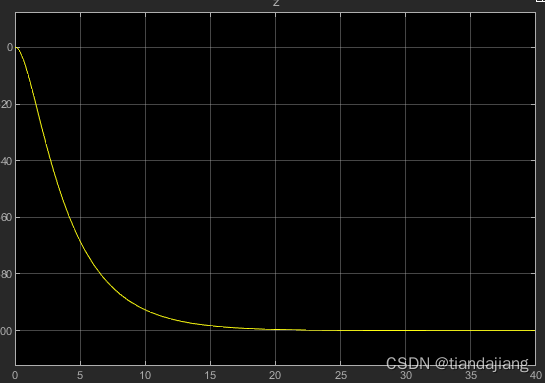
测得超调量为0%,调节时间14.6s
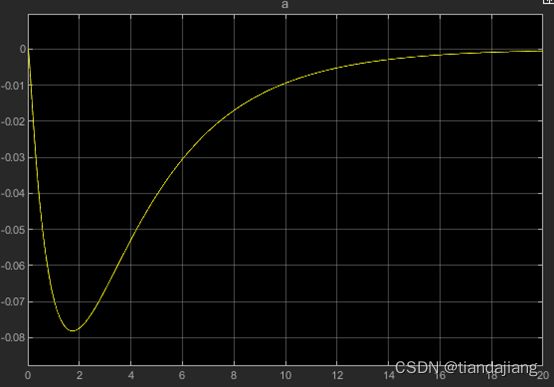
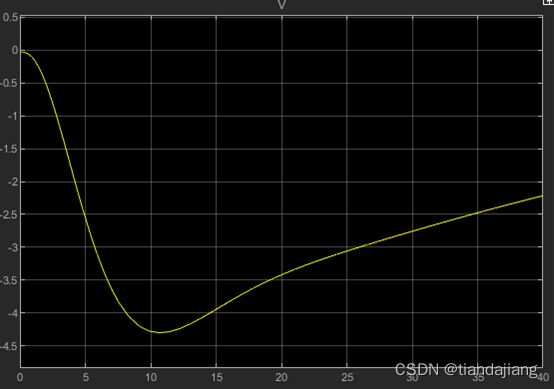
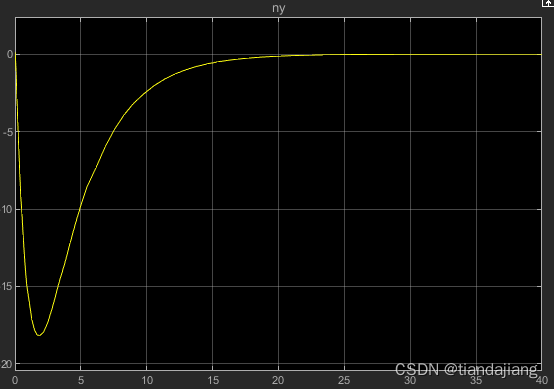
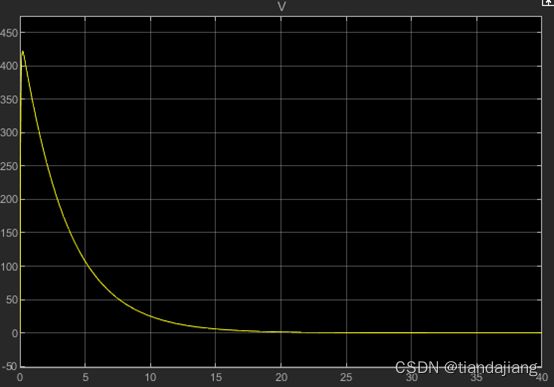
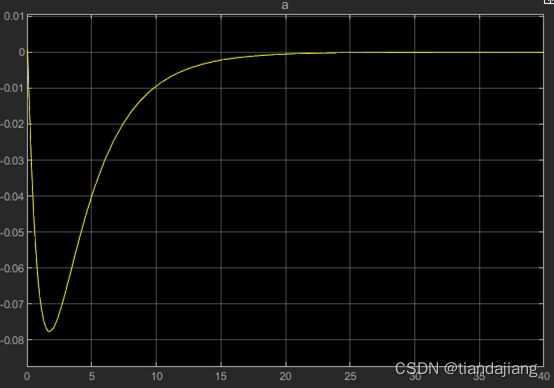
,纵向加速度极值18m/s^2,跟踪误差为0.0031m,速度在稳定后存在1.3m/s的余量,这是由于推力增加的结果。
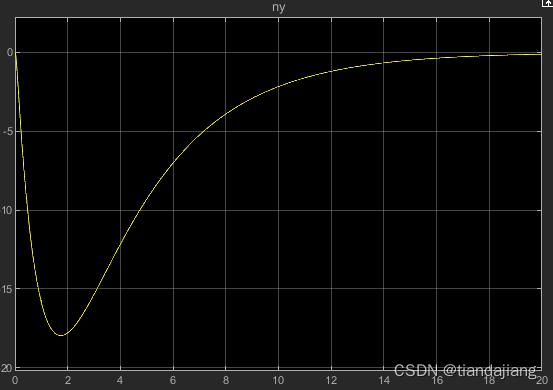
图 3 z方向变化曲线
图 4 z方向加速度
图 5 速度变化曲线
图 6 攻角变化曲线
图 7 δT推力变化曲线
图 8 simulink仿真稳定飞机位置变化
推力_增加高度模拟仿真视频:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-W9vuBMxp-1663160004199)(media/image11.emf)]
稳定性分析:**
系统根轨迹位于左半平面,系统任意配置均稳定,以下通过李雅普诺夫稳定性分析证明新系统稳定性。
利用matlab自带的lyap函数,通过[P]=lyap(A,Q),求得P。其线性定常系统稳定性判断为:
(1). A的所有特征根在左半平面
(2) 对任意正定矩阵Q,存在正定矩阵P满足:
A’P+PA=-Q
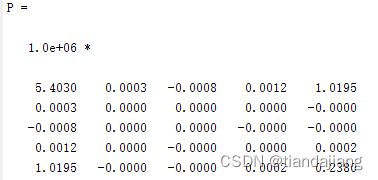
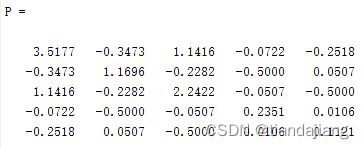
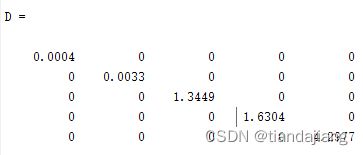
设Q=eye(5),lyap求得:
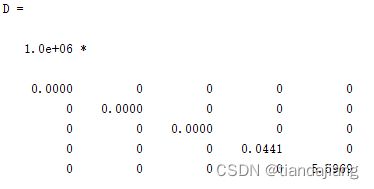
使用[V,D]=eig§函数求解P的特征值和特征向量,其中D为:
可得P为正定矩阵,A的根均位于左平面,A满足两要求,可以得出配置系统稳定。
结论:**
进行模拟仿真后,可以看到飞机高度上升过程飞行平稳且响应无震荡,飞机快速恢复稳定,且在规定的时间内达到跟踪误差0.0031m,超调量为0%,调节时间14.6s,,纵向加速度极值18m/s^2,速度在稳定后存在1.3m/s的余量,飞机高度增加100m相对位移增加1566m。
设计阻尼比为0,极点均小于要求,加速过载18m/s^2小于设计2G,符合题目所给设计要求。
系统2:输入:δe**
状态矩阵:Alo=
[-0.018 10.44 -9.797 0.153 -0.0001
-0.0003 -1.083 0 0.938 0
0 0 0 1 0
0 0 -2.622 -1.407 0
0 230 -230 0 0]
Bla=
[ 6.0178
-0.1256
0.0
-16.182
0]
Clo=[0 1 0 0 0
0 0 1 0 0]
Dlo=[0;0;0;0;0]
系统能控性分析:
rank(Uc)=5,可得系统可控
Renk(Os)=5,可得系统可观
图 9 根轨迹
由于存在右半平面根,所以只有当K值小于1630,系统稳定。
状态反馈器设计**
系统能观能控,可采用极点配置法和LQR配置法,这里使用LQR配置极点,为使得超调量小,调节时间短,飞行稳定,设置R=0.1
权重矩阵 Q= [1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 50000000 0
0 0 0 0 20]
配置得到反馈矩阵K=[-3 2861 -14389 -22384 14]
配置得到的极点为P=
[-100.09+0.15i;-100.09-00.15i;-99.82;-0.23+0.32i;-0.23-0.32i]
使用simulink搭建仿真模型
图 10 simulink仿真模型
测得超调量为4.62%,调节时间14.8s
,z方向加速度16.35m/s^2,跟踪误差为0.0006m,速度在稳定后存在-2.2m/s的相对变化,这是由于高度上升而推力不变的结果
图 11 z方向变化曲线
图 12 z方向加速度曲线
图 13 速度变化曲线
图 14 攻角变化曲线
图 15 Δe输入变化曲线
图 16 simulink仿真结果
Δe_增加高度模拟仿真视频:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eVaz07dy-1663160004212)(media/image23.emf)]
稳定性分析:**
由于系统根轨迹存在位于右半平面的根,需要保证开环增益小于1630,系统需要进行稳定性判断,以下通过李雅普诺夫稳定性分析证明新系统稳定性。
利用matlab自带的lyap函数,通过[P]=lyap(A,Q),求得P,D。其线性定常系统稳定性判断为:
-
A的所有特征根在左半平面
-
对任意正定矩阵Q,存在正定矩阵P满足:
A’P+PA=-Q
设Q=eye(5),lyap求得:
使用[V,D]=eig§函数求解P的特征值和特征向量,其中D为:
可得P为正定矩阵,且A配置所得的根位于左平面,满足两要求,可以得出配置系统稳定。
结论:**
进行模拟仿真后可以看到飞机高度上升过程飞行平稳,存在小幅震荡,飞机快速恢复稳定,且在规定的时间内达到远小于要求的误差,超调量为4.62%,调节时间14.8s,z方向加速度极值16.35m/s^2,跟踪误差为0.0006m,速度在稳定后存在-2.2m/s的相对变化,飞机稳定后迎角上升维持一定角度以保持高度,跟踪得到高度增加100m相对位移减少53m,相对速度减小2.3m/s。
设计主导极点阻尼比为0.32,小于设计要求,主导极点自然频率0.395,约等于设计要求,加速过载16.35m/s^2小于设计2G,满足设计要求
1,2系统共同作用**
输入:δT,δe
两控制系统均能稳定控制无人机高度变化,因此可以使用两种控制系统共同作用。
状态矩阵: Alo=[-0.018 10.44 -9.797 0.153 -0.0001
-0.0003 -1.083 0 0.938 0.00
0 0 0 1 0
0 0 -2.622 -1.407 0
0 230 -230 0 0]
Blo=[7.0609 6.0178
0 -0.1256
0 0
0 -16.182
0 0]
Clo=[0 1 0 0 0
0 0 1 0 0]
Dlo=[0 0;0 0;0 0;0 0;0 0]
设计反馈矩阵为
K=[-3 2861 -14389 -22384 14
3.2 -2700.3 4190 1034.9 -14.1]
超调量0,调节时间15s。
图 17 z方向高度变化曲线
图 18 z方向加速度曲线
图 19 速度变化曲线
图 20 攻角变化曲线
图 21 系统输入变化曲线
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i5ekzvF0-1663160004219)(media/image31.emf)]
**结论:**进行模拟仿真后飞机稳定后高度达到要求,飞机状态变量无明显变化,响应过程无震荡,可以得出在飞机上升过程中飞机推力起到主要作用,而舵偏角起辅助作用。
响应时间14.5s,加速过载18.2m/s^2,超调量为0,高度增加100m相对位移增加1553m,速度不变。
3.(2)纵向系统输入矩阵**
Ala2=[-0.3305 0.0426 0 -0.0011 -0.995
0 0 0 1 0
0 0 0 0 1
-38.658 0 0 -3.855 0.4958
14.418 0 0 0.0128 -0.509]
Bla2=[0.0161 0.0474
0 0
0 0
-59.804 11.958
-2.757 -5.682]
Cla2=[0 1 0 0 0
0 0 1 0 0]
Dla2=[0,0;0,0;0,0;0,0;0,0]
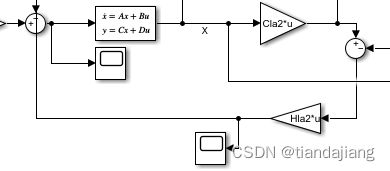
能控性分析:
Rank(Uc)=5,系统可控
能观性分析:
Rank(Os)=5,系统能观
状态观测器设计:**
系统状态空间模型:Xdot~=(A-HC)X~+Bu+Hy
A-HC极点决定了误差是否衰减,如何衰减,需要确定1个H矩阵保证A-HC稳定。
由于:det[sI-(A-HC)]=det[sI-(A’-C’H’)],因此,观测器极点配置问题可以转换为(A’,C’)极点配置问题,系统完全可观,即观测器配置矩阵完全可控,观测器可配置任意极点。
设状态观测器配置极点为P=[-1.3337+3.8299i;-1.3337-3.8299i;-7.4877+6.6460i;7.4877-6.6460i;-9.9309]
得到的配置矩阵 H=[-2.0825 -0.7835
12.0657 -0.1211
-0.1211 10.8135
67.7985 1.3210
-4.0921 8.4728]
图 22 状态观测器simulink仿真
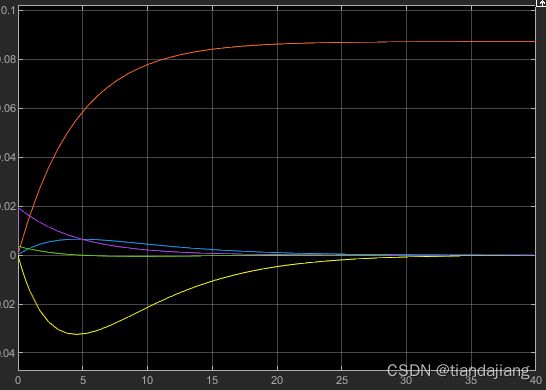
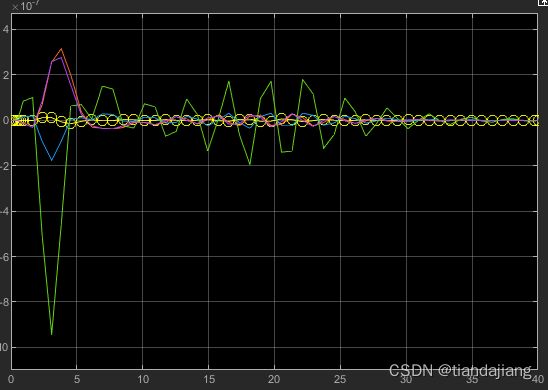
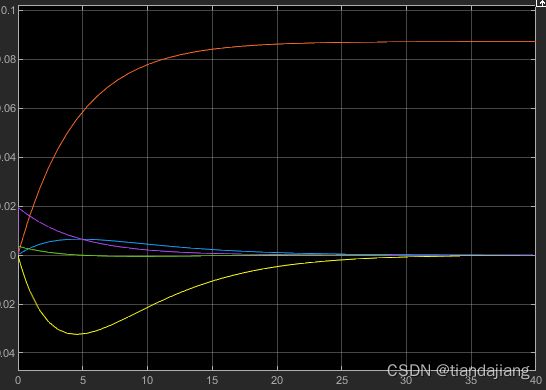
搭建过程中,状态空间模块使用全维输入全维输出的方式模拟积分环节,观测器状态变量误差均在10e-6的范围内,满足设计要求。
图 23 状态跟踪误差
图 24 状态变量变化曲线
观测器稳定性分析**
观测器进行稳定性判断,以下通过李雅普诺夫稳定性分析证明新系统稳定性。
利用matlab自带的lyap函数,通过[P]=lyap(A,Q),求得P,D。其线性定常系统稳定性判断为:
-
A的所有特征根在左半平面
-
对任意正定矩阵Q,存在正定矩阵P满足:
A’P+PA=-Q
设Q=eye(5),lyap求得:
使用[V,D]=eig§函数求解P的特征值和特征向量,其中D为:
可得P为正定矩阵,且A配置所得的根位于左平面,满足两要求,可以得出配置系统稳定。
总结:**跟踪误差小于10e-6,系统稳定,满足设计要求。
**反馈控制器设计:**A-BK
依据题目所给要求,阻尼比小于0.63.
反馈控制器极点P=[-901.4924;-413.5177;-0.4424;-0.2068;-0.2366]
反馈控制器配置矩阵K=[-0.1629 -2.9790 -11.7054 -6.5420 -51.1087
-2.3380 1.1574 -29.3766 2.5282 -131.8090]
图 25 反馈器Simulink仿真
图 26 观测器状态跟踪误差
图 27 状态变量变化曲线
图 28 状态变量 ψ 跟踪π 36 rad曲线
图 29 稳定后飞机位姿
结论:**可以看出系统超调量为0,响应时间为18.2s,系统快速达到稳定,响应过程稳定。
系统跟踪状态变量 ψ视频如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RlLkVnij-1663160004230)(media/image42.emf)]
状态反馈器稳定性分析**
观测器进行稳定性判断,以下通过李雅普诺夫稳定性分析证明新系统稳定性。
利用matlab自带的lyap函数,通过[P]=lyap(A,Q),求得P,D。其线性定常系统稳定性判断为:
-
A的所有特征根在左半平面
-
对任意正定矩阵Q,存在正定矩阵P满足:
A’P+PA=-Q
设Q=eye(5),lyap求得:
使用[V,D]=eig§函数求解P的特征值和特征向量,其中D为:
可得P为正定矩阵,且A配置所得的根位于左平面,满足两要求,可以得出配置系统稳定。
**总结:**跟踪误差小于10e-6,超调量为0,响应时间为18.2s,系统快速达到稳定,响应过程稳定,极点均无虚部,无阻尼比,满足设计要求。
题目涉及的matlab代码及simulink仿真:K3simulink仿真
lab自带的lyap函数,通过[P]=lyap(A,Q),求得P,D。其线性定常系统稳定性判断为:
-
A的所有特征根在左半平面
-
对任意正定矩阵Q,存在正定矩阵P满足:
A’P+PA=-Q
设Q=eye(5),lyap求得:
使用[V,D]=eig§函数求解P的特征值和特征向量,其中D为:

可得P为正定矩阵,且A配置所得的根位于左平面,满足两要求,可以得出配置系统稳定。
**总结:**跟踪误差小于10e-6,超调量为0,响应时间为18.2s,系统快速达到稳定,响应过程稳定,极点均无虚部,无阻尼比,满足设计要求。
题目涉及的matlab代码及simulink仿真:K3simulink仿真