总结神经网络中的正则化方法

正则化与过拟合

在论文中，正则化用“regularization”表示，那为什么需要正则化呢？因为神经网络在学习过程中出现了过拟合情况，具体表现就是在训练集上表现好，在测试集上预测能力差，就是我们所说的泛化能力差，说的更直白一些，就是举一反三的能力差，网络学到了一些不重要的信息，比如说，对于猫狗识别，由于种种原因，网络学习到猫的一项特征是胡须8-10根，下一次来了一只猫只有6根胡须，模型就判定不是猫，很显然这是不正确的，并且这项特征也是我们不需要的。

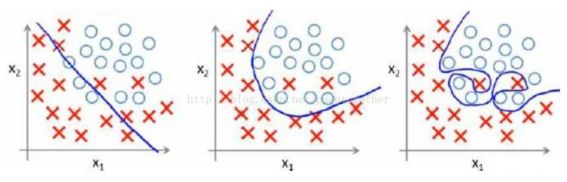
看一下下面这张图，最左边的是欠拟合，中间的就是正拟合，虽然有两个分错了，但也是能理解的，毕竟我们现实中的样本也是有很多干扰噪音的，最右边就是过拟合了，样本的什么特征都给学出来了。

正则化就是针对特征，针对模型的一种限制算法。拟合能力越强，说明到学习的特征越多，w参数数量越多，模型越复杂。常用的正则化方法有数据增强、L2 正则化（权重衰减）、L1 正则化、Dropout、Drop Connect、BN、随机池化和提前终止等。下面重点来讨论一下L1、L2正则化、Dropout、BN这三种方法。

图转载链接：https://www.zhihu.com/question/20924039/answer/131421690

L1、L2正则化

在机器学习中，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归），具体使用方法就是直接将L1、L2作为惩罚项添加在损失函数后，限制权重的输出，同时也可以降低模型的复杂度，使得模型在复杂度和性能之间达到平衡。具体公式如下：

L1正则：表达式为α乘以权值向量w各元素绝对值和，L1会将对模型特征表达影响较小的权值变为0，产生一个稀疏矩阵。L2正则：表达式为α乘以权值向量w各元素的平方和开根，会对网络一些大数值的参数进行惩罚，可以理解为：L2正则就是使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征。

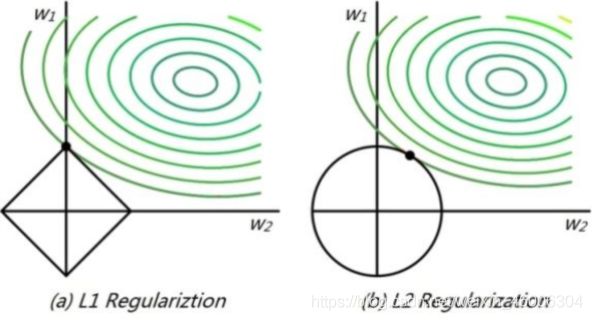
由于L1正则化约束的解空间是一个菱形，所以等值线与菱形端点相交的概率比与线的中间相交的概率要大很多，端点在坐标轴上，一些参数的取值便为0。L2正则化约束的解空间是圆形，所以等值线与圆的任何部分相交的概率都是一样的，所以也就不会产生稀疏的参数。具体可参考下图。

图转载链接：https://blog.csdn.net/yimingsilence/article/details/82027474

Dropout

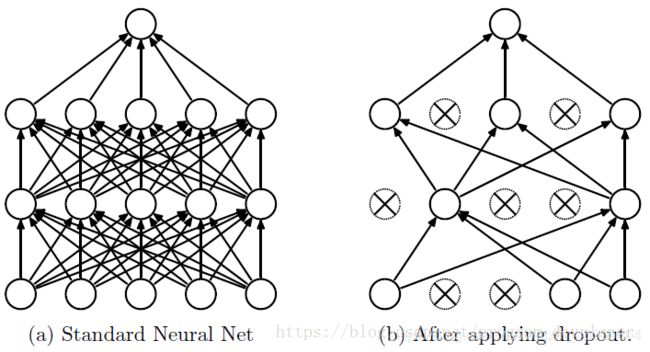
Dropout是Hinton在其论文《Improving neural networks by preventing co-adaptation of feature detectors》中提出的。在每次训练的时候，让神经元以一定的概率失活，这样就可以打破神经元之间的相互依赖性，这个神经元学习到的特征不再与固定的输入有关，而是随机的，迫使网络学习到一些更加鲁棒的特征。一般来说，选择的Dropout率为0.5，因为这样随机性最强。

可以看到，神经元失活后，网络变得更加简单，每一次前向传播，网络都能学到不同的特征。

那为什么Dropout能防止过拟合呢？总结起来大概有两方面的原因：

1、类似于Bagging的平均作用：先回顾一下Bagging的原理，Bagging是集成学习中的典型算法，对于给定的n个样本，我们随机抽取m（m＜n）个样本作为训练集，先训练一个独立的估计器，然后将抽取的样本放回，再随机抽取m个样本再次训练一个独立的估计器，这样重复多次，最终训练出多个弱估计器，然后将这些弱估计器联合起来使用，对于分类问题，采取“少数服从多数”的原则，对于回归问题，采取取平均的方法。对于Dropout后的神经网络也大致相同，每一次Dropout以后的网络就相当于不同数据训练的弱估计器，就算某一个或几个训练出来的小模型出现了过拟合，只要其他的小模型是正常的，这对最终的预测是没有太大影响的。

2、类似于L1、L2正则化的参数限制作用：由于dropout导致两个神经元不一定每次都在一个小模型网络中出现，这样就限制了某些特征只有在特定特征下才产生效果的情乱，迫使网络学习更加具有鲁棒性的特征，并且每一次Dropout后的神经元都是随机组合的，学习到的特征也同时具有多样性，这和L1、L2正则化类似，减小或去除某些不利于网络的参数，只不过这种减小或去除是随机的。

Batch Normalization

Batch Normalization是2015年一篇论文中提出的数据归一化方法，往往用在深度神经网络中激活层之前。其作用可以加快模型训练时的收敛速度，使得模型训练过程更加稳定，避免梯度爆炸或者梯度消失，并且起到一定的正则化作用，几乎可以取代Dropout

对于BN这个大杀器，我们必须要了解其提出的原因和原理：

随机梯度下降法（SGD）对于训练深度网络简单高效，但是它有个毛病，就是需要我们人为的去选择参数，比如学习率、参数初始化、权重衰减系数、Dropout比例等。这些参数的选择对训练结果至关重要，以至于我们很多时间都浪费在这些的调参上。那么使用BN（详见论文《Batch Normalization_ Accelerating Deep Network Training by Reducing Internal Covariate Shift》）之后，你可以不需要那么刻意的慢慢调整参数。

神经网络一旦训练起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal  Covariate Shift”。Paper所提出的算法，就是要解决在训练过程中，中间层数据分布发生改变的情况，于是就有了BN这个牛逼算法的诞生。

以上两段参考连接：https://www.cnblogs.com/wangzhongqiu/p/10234265.html，这篇文章分析的相当透彻，建议大家可以看看。

对于BN是如何防止过拟合的，国外大牛有这么一个解释：

When training with Batch Normalization, a training example is seen in conjunction with other examples in the mini-batch, and the training network no longer producing deterministic values for a given training example. In our experiments, we found this effect to be advantageous to the generalization of the network.

大概意思是：在训练中，BN的使用使得一个mini-batch中的所有样本都被关联在了一起，因此网络不会从某一个训练样本中生成确定的结果。

这句话什么意思呢？意思就是同样一个样本的输出不再仅仅取决于样本本身，也取决于跟这个样本属于同一个mini-batch的其它样本。同一个样本跟不同的样本组成一个mini-batch，它们的输出是不同的。由于训练时样本是随机打乱的，每一次抽取到进行训练的样本也是不同的，这样对于网络来说就能从无数个不同的组合中提取到更加鲁棒的特征。相比于Dropout、L1、L2正则化来说，BN算法防止过拟合效果没那么明显。

对于其他的防止过拟合方法，这里就暂时先不做讨论了，也没有那么重要了。