Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

Swin Transformer: Shifted Windows

Introduction

• 在视觉领域使用 Transformer 存在如下挑战：(1) 在已有的 Transformer 模型中，不同层级的 Transformer block 中的 tokens 感受野相同，均代表固定大小的 patch，不利于学习多尺度特征，不适合检测分割等密集预测任务；(2) 图片分辨率很大时 Transformer 需要巨大的算力 (自注意力的计算复杂度是图片大小的平方)
• 为了解决上述问题，作者提出了一种通用的 backbone Swin Transformer，它能像 CNN 一样做层级式的特征提取 (能提取出多尺度的特征)，同时相对图片大小具有线性计算复杂度

Method

Hierarchical feature maps and Linear computational complexity

Patch merging

• Swin Transformer 从小尺寸 patch 开始 (shown in gray)，随着层数的加深不断合并相邻的 patches 来增大 patch (i.e. token) 的感受野 (注意如下图所示，合并的 patch 为相隔一格的 patch)，进而提取出多尺度特征图 (每个 patch 为 $4\times 4$ 的图像块，下图中的 4x, 8x, 16x 代表下采样率)。有了多尺度特征图后，Swin Transformer 可以很容易地与 feature pyramid networks (FPN) / U-Net 等检测 / 分割网络结合，也可以仅使用最后一层的特征图经全局平均池化和线性层后做图像分类
  

CNN 的池化操作使得模型后面的特征感受野增大，所以具备了平移不变性。而 Swin Transformer 由于有了 patch merging 操作，所以 token 的感受野也增大了，也具备了一定的平移不变性

Self-attention in non-overlapped windows

• Self-attention in non-overlapped windows：Swin Transformer 将自注意力的计算限制在了 local window (shown in red) 内，每个 local window 中都有 $M\times M$ 个 patches (typically, $M=7$; 当 $h,w$ 不能被 $M$ 整除时会在右下进行 padding)，位于不同 local windows 中的 patches 之间不进行自注意力计算，这样 Swin Transformer 的计算复杂度相对图片尺寸就为线性的。同时，在同一个 window 中计算自注意力也有利于 memory access，进一步加速了计算过程。并且这样的设计还相当于给 Swin Transformer 加上了 locality 的先验知识
  下面可以对比一下 MSA (Multi-head Self attention) 和 W-MSA (Multi-head Self attention with local windows) 的计算复杂度：
  可以看到，MSA 的计算复杂度是 patch 数 $hw$ 的二次方，而 W-MSA 的计算复杂度则是线性的。由于 $M^2$ 远小于 $hw$，W-MSA 的计算复杂度远小于 MSA
  • $\Omega (\text{MSA})$: 设有 $n$ 个 head，每个 head 均在 $d_h$ ($C=n\times d_h$) 维的子空间内计算自注意力。对于 $hw\times C$ 的输入特征图，$Q,K,V$ 矩阵均为 $hw\times C$，多头自注意力层首先用 3 个 $C\times C$ 的矩阵将 $Q,K,V$ 分别映射到 $n$ 个子空间中得到 3 个 $hw\times n{d}_h$ 的 $Q,K,V$ 矩阵，矩阵的每 $n$ 列即为一个 head 的 $Q,K,V$，所需乘法次数为 $3hw{C}^2$. 在每个 head 内，$Q,K,V$ 均为 $hw\times d_h$，计算 $hw\times hw$ 的 Attention matrix 所需乘法次数为 $(hw{)}^2{d}_h$，计算 $hw\times d_h$ 的输出所需乘法次数为 $(hw{)}^2{d}_h$，因此每个 head 所需乘法次数为 $2(hw{)}^2{d}_h$，所有 heads 所需乘法次数为 $2(hw{)}^2{d}_h\times n=2(hw{)}^{2}C$，最终将所有 heads 的输出连接在一起得到 $hw\times n{d}_h$ 的输出映射回原 $C$ 维空间所需乘法次数为 $hw\times n{d}_h\times C=hw{C}^2$，因此总的计算复杂度为 $4hw{C}^2+2(hw{)}^{2}C$
  • $\Omega (\text{W-MSA})$: 一个窗口内有 $M^2$ 个 tokens，代入 $\Omega (\text{MSA})$ 的计算公式可知一个窗口内多头自注意力的计算复杂度为 $4M^2{C}^2+2(M^2{)}^{2}C$。一共有 $h/M\times w/M$ 个窗口，因此总的计算复杂度为 $(4M^2{C}^2+2(M^2{)}^{2}C)\times h/M\times w/M=4hw{C}^2+2M^{2}hwC$
• Relative position bias: 在计算自注意力时，Swin Transformer 还加入了 relative position bias $B\in {\mathbb{R}}^{M^2\times M^2}$，直接将 $B$ 加在 $M^2\times M^2$ 的 Attention Matrix 上：
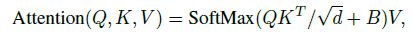  而在每个轴上，相对位置只可能位于 $[-M+1,M-1]$，因此可以构造一个更小的矩阵 $\hat{B}\in {\mathbb{R}}^{(2M-1)\times (2M-1)}$，$B$ 中的值可以从 $\hat{B}$ 中获得。由于 $\hat{B}$ 是一个 learnable matrix，模型可以自己学得一个窗口内不同 patches 之间的相对距离，同时通过将相对距离加在 Attention matrix 上，self-attention 就可以进一步融合位置信息。当微调的 window size 和预训练的 window size 不同时可以使用二次或三次插值

shifted window

• 如果仅采用上述 local window 的机制，虽然减少了计算量，但不同窗口之间也缺少交互，模型难以学习全局特征，为此 Swin Transformer 引入了 shifted window 来使得原本属于不同窗口之间的 patches 也能进行交互。如下图所示，通过将上一层中 $M\times M$ 的 local window 向右下方移动 $(\lfloor \frac{M}{2}\rfloor ,\lfloor \frac{M}{2}\rfloor )$ 个 patches，原本无法进行交互的 patch 之间也能进行自注意力计算了 (在移动窗口时甚至可以随机位移达到一种 stochastic depth 的作用)
  
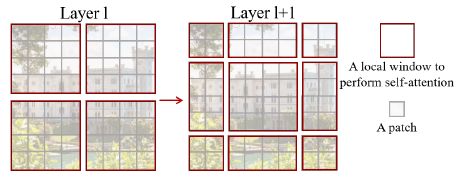
• Efficient batch computation for shifted configuration: shifted window 会使得窗口数从 $\lceil \frac{h}{M}\rceil \times \lceil \frac{w}{M}\rceil$ 增加到 $(\lceil \frac{h}{M}\rceil +1)\times (\lceil \frac{w}{M}\rceil +1)$，其中的一些 windows 会变得比 $M\times M$ 更小。如果想要将所有窗口放在一个 batch 内计算自注意力，一种简单的方法是将所有窗口大小都 pad 到 $M\times M$ 然后在计算自注意力的时候 mask padded value，但这样开销太大，例如上图中原本只需要计算 4 个窗口，现在却需要计算 9 个窗口，计算量变为了原来的 2.25 倍。为此，作者提出了一种更高效的批计算方法，先使用 cyclic shift 将原特征图进行移位，然后对每个窗口内进行 masked MSA，最后再用 reverse cyclic shift 恢复特征图顺序：
  具体来说，循环移位后同样可以划分为 4 个 window。考虑 Window2，在计算自注意力时需要将 $M\times M\times C$ 的输入 reshape 为 $M^2\times C$，其中前 $M^2/2$ 个 tokens 属于区域 3，后 $M^2/2$ 个 tokens 属于区域 6，由于区域 3 和区域 6 之间不需要计算自注意力，因此 Attention Matrix 对应的 Attention Mask 如下图所示，只在区域 3 和区域 6 内部计算自注意力，紫色区域为一个很大的负数表示不需要计算自注意力。再考虑 Window1，reshape 后 $M/2$ 个 tokens 属于区域 1，$M/2$ 个 tokens 属于区域 2，依次不断交替，因此最后的 Attention Mask 如下图所示，只在区域 1 和区域 2 内部计算自注意力
  

The shifted window approach also proves beneficial for all-MLP architectures

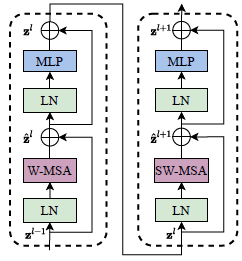
Two Successive Swin Transformer Blocks

• Swin Transformer 使用了两个连续的 Transformer 块来进行 W-MSA (multi-head self attention modules with regular windowing configurations) 和 SW-MSA (multi-head self attention modules with shifted windowing configurations)，也就是先在 local window 内计算自注意力，然后在 shifted local window 内计算自注意力

Overall Architecture

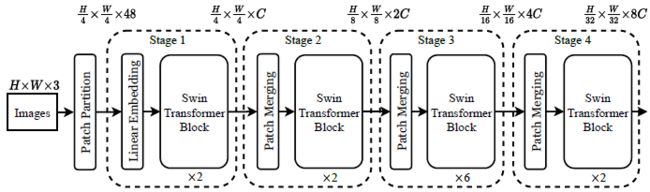
• Patch partition: Swin Transformer 的 patch 大小为 $4\times 4$，因此输入的 RGB 图像进行 patch partition 之后 size 变为 $\frac{H}{4}\times \frac{W}{4}\times 48$，每个 patch 都看作一个 token，特征维度为 $4\times 4\times 3=48$
• Stage 1: 先用一个 linear embedding 层将 raw-valued feature 投影到指定维度 $C$ (默认设置为 $48\times 2=96$)，size 变为 $\frac{H}{4}\times \frac{W}{4}\times C$，再经过两个连续的 Swin Transformer Block (W-MSA + SA-MSA) 得到最终输出
• Stage 2 (Stage 3, 4): 先进行 Patch Merging 增加 token 的感受野，合并相邻的 4 个 patches，size 变为 $\frac{H}{8}\times \frac{W}{8}\times 4C$，然后利用线性层让输出维度变为 $2C$，size 为 $\frac{H}{8}\times \frac{W}{8}\times 2C$，再经过两个连续的 Swin Transformer Block (W-MSA + SA-MSA) 得到最终输出。可以看到，这里的设计与 CNN 类似，每个 stage 都是将特征图大小减半，通道数乘二，输出的特征图大小与 VGG、ResNet 等典型的 CNN 网络相同，因此可以很方便地用 Swin Transformer 去替代 CNN 作为其他任务的 backbone

注意，只在 Stage 3 增加 Swin Transformer Block 数，这样效果最好，最新的 convnext 论文也基于这个观察，把 resnet 每个 stage 里的 block 数也改动了

---

Architecture Variants

Swin-T(iny) 和 Swin-S(mall) 的模型大小分别接近于 ResNet-50 和 ResNet-101；Swin-B(ase) 的模型大小接近于 ViT-B/DeiT-B

Experiments

Image Classification on ImageNet-1K

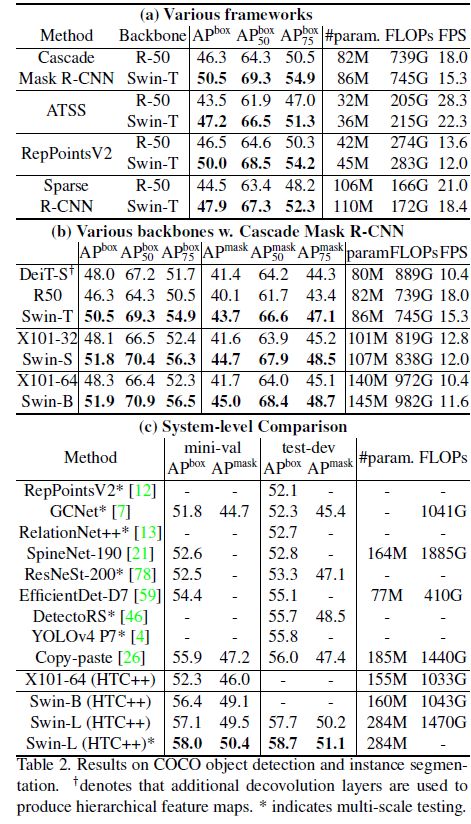
Object Detection on COCO

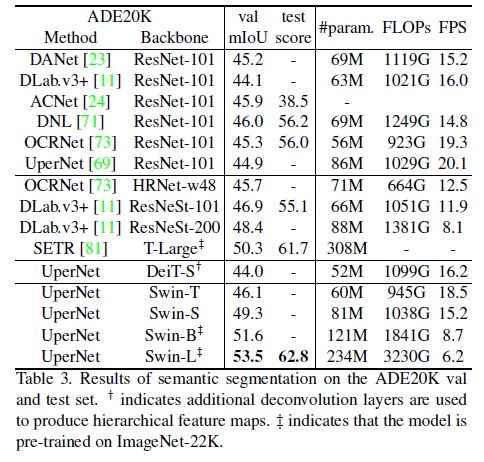
Semantic Segmentation on ADE20K

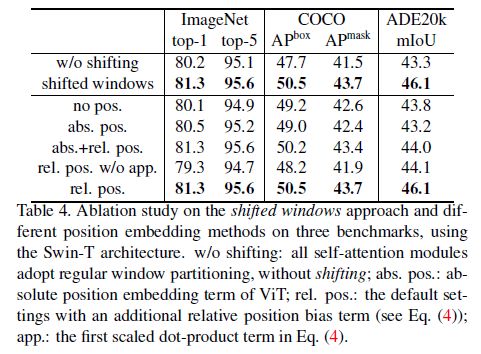
Ablation Study

Third-party Usage and Experiments

References

• paper: Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
• code and models: https://github.com/microsoft/Swin-Transformer
• Swin Transformer 论文精读【论文精读】