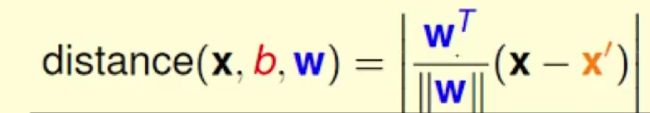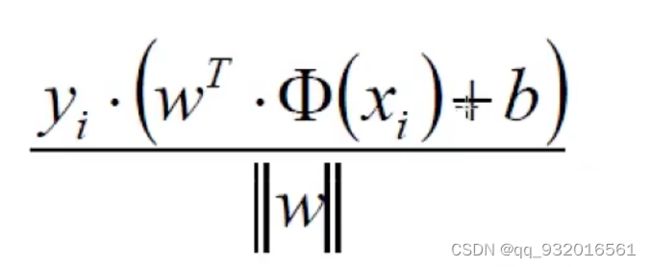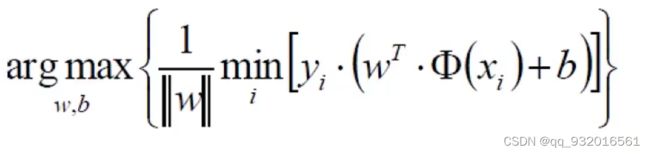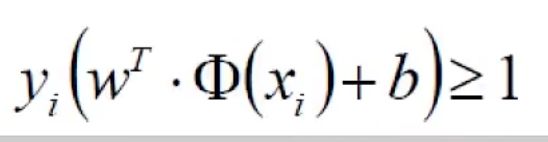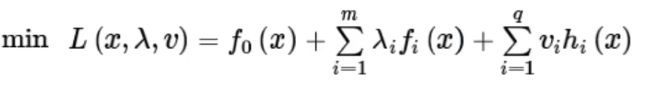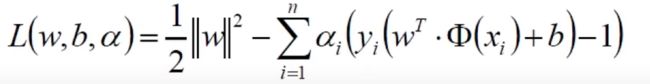机器学习算法----支持向量机SVM (软间隔、核函数、拉格朗日乘子法) (学习笔记)
文章目录
- 距离计算
- 优化目标
-
- 拉格朗日乘子法
- 软间隔(soft-margin)
- 核函数
- 学习参考
昨天整理了一下聚类算法的笔记----------各种聚类算法总结
今天整理一下同为分类的另一个算法（有监督）:
支持向量机(Support Vector Machine)
距离计算
分类都绕不开一个问题就是样本间距离的计算，看下面这张图。
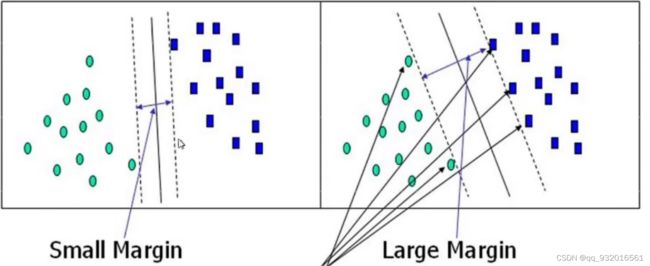
显然右边分隔线的间距更大，更加有容错率。
如何计算距离？
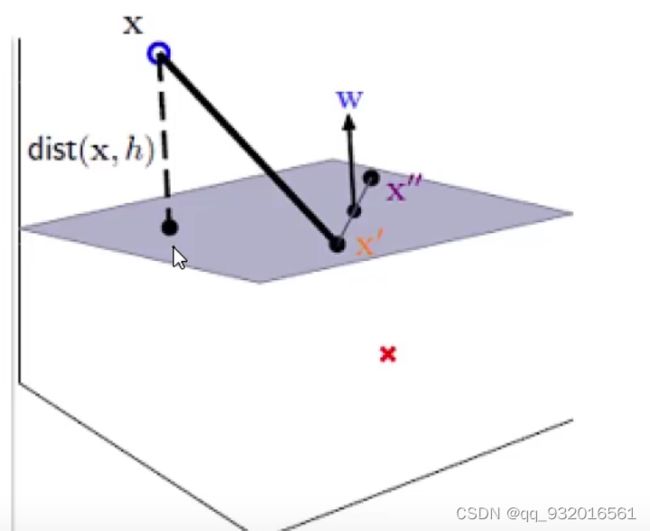
下图是一张三维图。
假设样本点为 X X X，灰色的纸面是分割面，类似于上面的二维图中的分割线。 X ′ X' X′ X ′ ′ X'' X′′ 都是分割面上的点。
如何求样本点 X X X 到风格面的距离呢？显然可以直接垂直求点到面的距离dist。不过这样较为复杂，可以先求 X X X到点 X ′ X' X′ 的距离， 两点间的距离比较容易计算，然后将该线段投影到垂线的方向(法向量的方向W)。
参考公式：
法向量除以自身的模=单位方向向量
将式子展开， 有
- 1 f ∣ ∣ W ∣ ∣ ( W T X − W T X ′ ) \frac {1}f {||W||}(W^TX-W^TX') f1∣∣W∣∣(WTX−WTX′) 。记为(1)式
- 因为 X ′ X' X′ X ′ ′ X'' X′′都是平面上的点，故有:
- W X ′ + B = 0 WX'+B=0 WX′+B=0 .。记为(2)式
- W T X ′ = − b W^TX' = -b WTX′=−b. 。记为(3)式
- 将(3)式代入(1)式中，最终得到: 1 ∣ ∣ W ∣ ∣ ∣ ( W T X + b ) ∣ \frac {1} {||W||}|(W^TX+b)| ∣∣W∣∣1∣(WTX+b)∣
优化目标
再来看一下刚开始的那张图
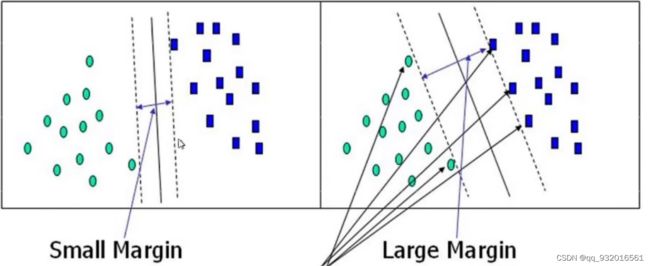
要达到右边的目的，用一句话描述:我们要找到一条线，使得离该线最近的点距离最远！！
上面那句话多读两遍，配合图看，理解清楚，这就是最终要最到的目的。
现在假设一个数据集来推出最后的目标优化公式:
(X1,Y1),(X2,Y2)…
Y为样本类别 X为正例时Y = 1 反之为 Y = -1。
既:
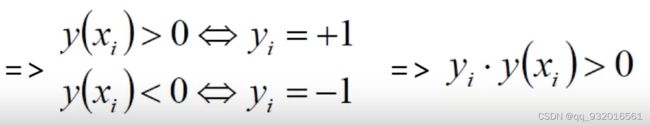
这样操作过后就可以去掉一开始距离公式中的绝对值了。
将公式化简得到:
得到优化目标公式:
再把上面那句话贴过来,
我们要找到一条线，使得离该线最近的点距离最远!
min那里一大串都是等于>=1的（放缩，令其>=1），最小值就是1了，所以满足条件下最终考虑目标优化公式:
- a r g m a x 1 ∣ ∣ W ∣ ∣ argmax \frac{1}{||W||} argmax∣∣W∣∣1
既求 ∣ ∣ W ∣ ∣ ||W|| ∣∣W∣∣ 的极小值。
化简模向量 ∣ ∣ W ∣ ∣ ||W|| ∣∣W∣∣ = W 2 W^2 W2 前面可以加任何常数，比如二分之一 八分之一啥的，毕竟W是向量且这里是找wx+b中的w和b参数，使得求出最小值(极小值)。
拉格朗日乘子法
拉格朗日乘子法求 ：求带约束条件下的极值问题。
这里的约束条件就是上面求优化目标的时候 ，放缩过程令那min那块>=1 的那一部分:就是下面这一块
约束条件
求解过程基本思路就是，引入了一个新的变量设为a，找到a和原始要求的w与b之间的关系，然后将a替换掉原始式子中的w和b，并求出a，再将wb代回。
原子转换公式:
代入:
其中i代表数据中的每一个样本。
对目标参数w和b求偏导，看到这有一个KKT的问题，我尝试看了看没看懂，劝退了。
关于KKT对偶问题
软间隔(soft-margin)
看下面这张图。
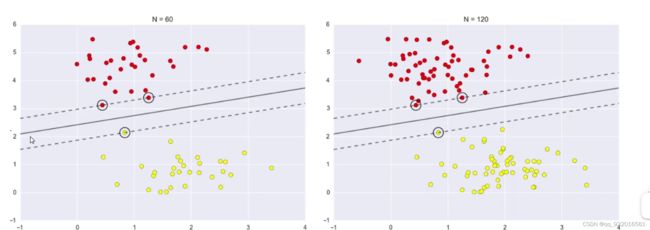
左边有60个数据样本，右边有120个数据样本，但是分割线却没发生改变。
说明真正发挥作用的数据点是距离分割线最近的那几个点。
也印证了为啥叫支持向量机。起到支撑 支持构建中间的分割向量的数据的点。
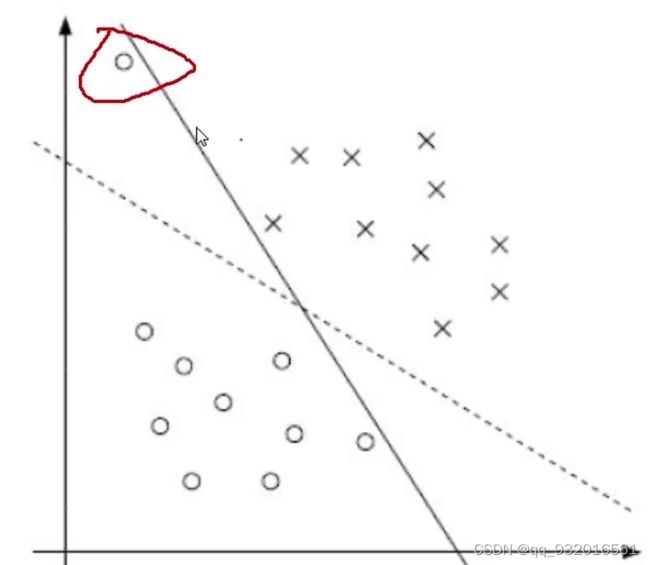
在看下面这张图，
显然有一个异常点(离群点),如果考虑该异常点，则导致分割线不是那么好，如果不考虑就是图中的虚线，这个虚线是比较好的。所以有了软间隔。
加入软间隔的目的就是希望模型别太受到异常点(噪音)的影响。
所以引入了一个叫松弛因子的东西，给分割线一些容忍度。
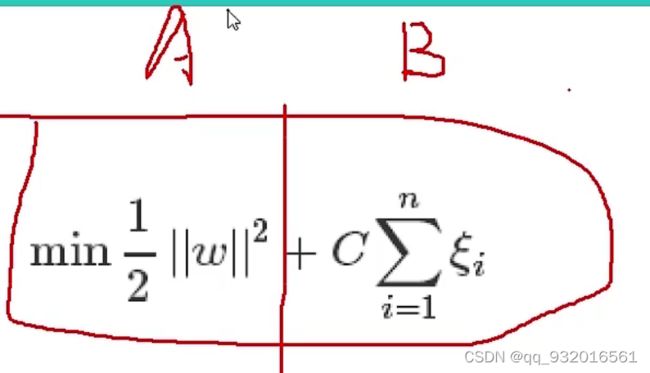
就有了加入松弛因子之后的目标参数:
A上面说过了，B部分就是引入的松弛因子。
其中C参数越小，意味着有越大的容忍度。
核函数
前面得到了一个目标优化公式,就是下面这个:
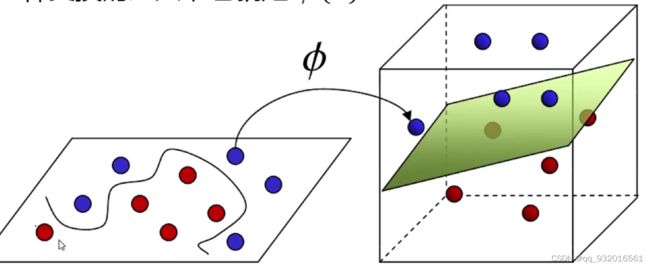
这里面有一个参数，就是 Φ参数（核函数）。
看下面这个图，如果在二维平面上分开红蓝点，所描绘出来的分割线是比较难的(过拟合、复杂计算量)，于是通过了 Φ 将他变成了三维上，用一张纸(平面)就分开了。
高斯核函数(应用最广泛，可无脑用):
是一个非线性决策边界。
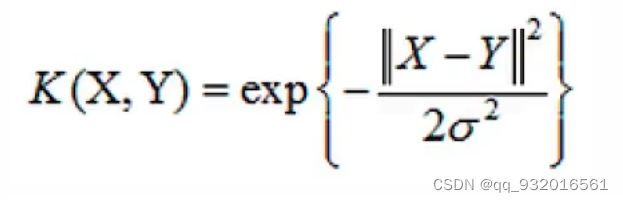
式子展开就是泰勒基数。无限逼近嘛，所以这里面有个调参 就分母上的那个西格玛，调的越大，就越复杂，过拟合风险越高。
学习参考
KKT对偶问题:https://www.stat.cmu.edu/~ryantibs/convexopt/lectures/kkt.pdf
拉格朗日乘子法:https://www.cnblogs.com/mo-wang/p/4775548.html
视频教程 :https://www.bilibili.com/video/BV1ma411h7wW?p=4&spm_id_from=pageDriver
核函数详解:https://blog.csdn.net/kateyabc/article/details/79980880