用R语言实现环境流行病学中的时间序列回归:以2002-2006年伦敦数据集为例
用R语言实现环境流行病学中的时间序列回归:以2002-2006年伦敦数据集为例
- 一、数据说明
- 二、描述性分析
- 三、时间序列回归
-
- 泊松回归
- 四、控制季节性和长期趋势
-
- (一)Option 1:时间分层模型 (Time stratified model)
- (二)Option 2:周期函数-傅里叶项 (Periodic functions-Fourier terms)
- (三)Option 3:灵活的样条函数 (Flexible spline functions)
- (四)围绕长期模式的残余变化
- 五、暴露结果关联和混杂
-
-
- 1. 臭氧
- 2. 其他时变因素的混淆
-
- 六、允许延迟曝光效果
-
- (一)单滞后模型 (SINGLE-LAG MODELS)
- (二)分布滞后模型 (UNCONSTRAINED DLM)
- (三)受约束的分布滞后模型 (CONSTRAINED (LAG-STRATIFIED) DLM)
- (四)Short-term displacement, or ‘harvesting’
- 七、模型检查和敏感性分析
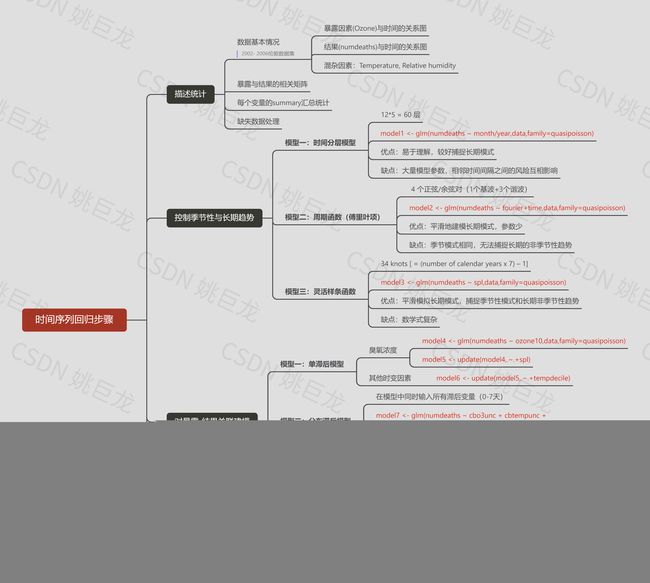
- 八、思维导图总结
- 参考文献
时间序列回归是环境流行病学中常用的研究设计方法。该方法经常用于量化环境暴露(如空气污染、花粉、灰尘和天气变量)与健康结果的短期关联的研究。
本文旨在用R软件来复现一个经典例子中的数据分析方法。该例子来源于下面这篇文章:
一、数据说明
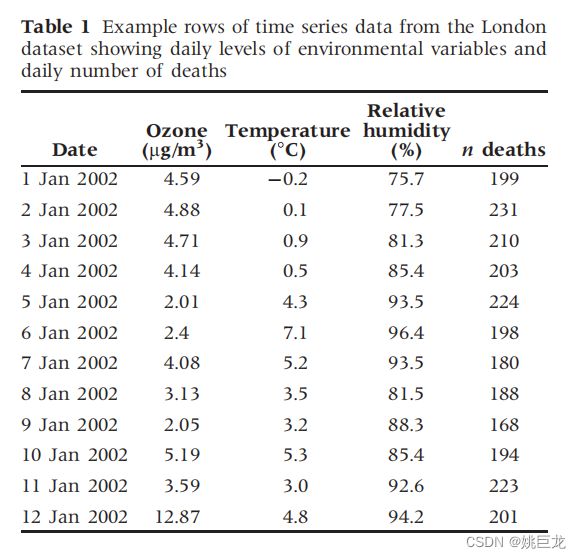
伦敦数据集的时间序列回归分析:
- 数据集由 2002 年 1 月 1 日至 2006 年 12 月 31 日期间每天的一次观测组成
- 每天都会测量当天的(平均)臭氧水平,以及该市发生的死亡总数
- 本研究要解决的问题是 “臭氧水平的日常变化与每日死亡风险之间是否存在关联?” 因此,感兴趣的接触是臭氧浓度(Ozone (µg/m3)),结果是死亡(n deaths)
- 该数据集还包含两个潜在混杂因素的每日测量值,即温度(Temperature (°C))和相对湿度(Relative humidity (%))
在R中导入数据:
library(foreign)
data <- read.dta("londondataset2002_2006.dta")
options(na.action="na.exclude")
二、描述性分析
summary(data)
library(epiDisplay)
des(data)
summ(data)
cor(data[,2:4])
——————————————————————————————【运行结果】——————————————————————————————————
> des(data)
No. of observations = 1826
Variable Class Description
1 date Date
2 ozone numeric Ozone level in ug/m3
3 temperature numeric Temperature in deg C
4 relative_humidity numeric Relative humidity in %
5 numdeaths integer N deaths
> summ(data)
No. of observations = 1826
Var. name obs. mean median s.d. min. max.
1 date 1826 12600.5 12600.5 <NA> 11688 13513
2 ozone 1826 34.77 34.92 18.3 1.18 119.25
3 temperature 1826 11.72 11.47 5.65 -1.4 28.17
4 relative_humidity 1826 69.1 69.61 13.7 31.23 98.86
5 numdeaths 1826 149.51 148 20.7 99 280
> cor(data[,2:4])
ozone temperature relative_humidity
ozone 1.0000000 0.4560300 -0.5269955
temperature 0.4560300 1.0000000 -0.4442078
relative_humidity -0.5269955 -0.4442078 1.0000000
绘制整个研究期间暴露(臭氧)和结果(死亡人数)随时间变化的散点图:
oldpar <- par(no.readonly=TRUE)
par(mex=0.8,mfrow=c(2,1))
plot(data$date,data$numdeaths,pch=".",main="Daily deaths over time",
ylab="Daily number of deaths",xlab="Date")
abline(v=data$date[grep("-01-01",data$date)],col=grey(0.6),lty=2)
plot(data$date,data$ozone,pch=".",main="Ozone levels over time",
ylab="Daily mean ozone level (ug/m3)",xlab="Date")
abline(v=data$date[grep("-01-01",data$date)],col=grey(0.6),lty=2)
par(oldpar)
layout(1)
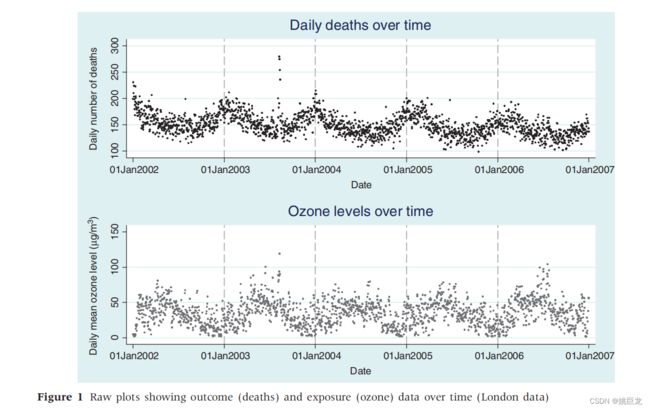
散点图结果显示:臭氧水平和死亡人数似乎都受年度季节性模式的支配,夏季臭氧最高,冬季最低,而死亡模式则相反。
根据这两张图,我们可以初步得到一个推断是:冬季臭氧水平低是死亡率较高的“原因”。
很明显这个推断是有问题的,产生这个问题的原因可能是由于这个长期的时间序列里面,有其他的系统模式存在,诱导了这样一个相关性。
所以,我们的研究方向不应该放在这一整个长期的时间序列上,而是要在相对比较短的时间序列上去看臭氧浓度和死亡人数的关系。
这也就是为什么在后面要去消除季节性和长期趋势的影响。
三、时间序列回归
- 回归的主要目的是调查:结果的某些短期变化是否可以通过主要暴露的变化来解释,即在该数据集中,日常死亡人数的变化是否可以由空气中臭氧水平的变化来解释。
- 回归方法的使用还可以控制多个潜在的混杂因素。
泊松回归
这里的结果变量是计数型变量(每天的死亡人数)。分析计数型数据的常用回归方法是泊松回归。这种类型的时间序列数据有一些独特特征:
- 包括季节性在内的长期模式可能会主导数据。由于我们对短期关联感兴趣,因此目标是消除(即控制)这些长期模式,并查看感兴趣的风险是否解释了一些剩余的短期变化。
- 原始数据中违反了泊松回归的假设:观测不太可能是独立的,时间上接近的观测可能比时间上遥远的观测更相似。
- 数据倾向于“过度分散”,这意味着结果计数的方差高于泊松分布下的预测值(其中方差 = 均值),因此有必要进行简单的调整以获得模型中的适当标准误差拟合。
四、控制季节性和长期趋势
要解决的研究问题是结果的短期变化是否可以通过兴趣暴露来解释?即在我们的示例中,死亡率的日常变化是否与每日臭氧水平有关。但原始结果数据可能最初由季节性模式和长期趋势主导,因此有必要在回归模型中控制这些模式,以便有效地将它们与短期关联区分开来在我们感兴趣的曝光和结果之间。
(一)Option 1:时间分层模型 (Time stratified model)
-
第一个方法是时间分层模型。既然,原始数据可能是由季节性和长期趋势主导,那我们就把这些数据分开,在短期里面去看臭氧和死亡人数之间的关系。
这里需要创建两个新的变量,month 和 year; -
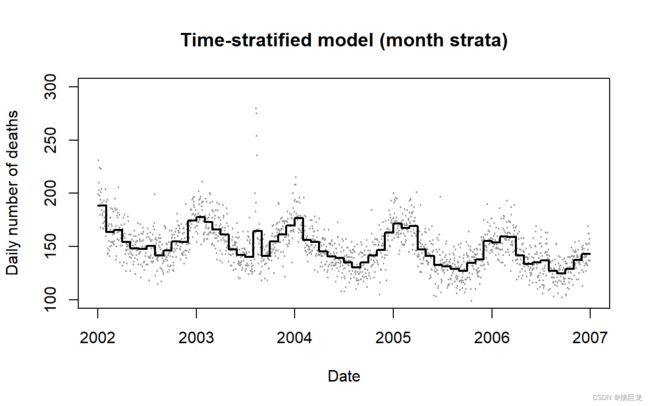
在结果数据中对长期模式进行近似建模的一种简单方法是将研究期分成多个区间,并为每个区间估计不同的基线死亡风险。在实践中,这意味着简单地在泊松模型中为每个时间间隔包含一个指示变量。每日数据时间间隔的一种可能选择是经过的日历月,这样在这些数据中就有 12 X 5 = 60 个层。
# OPTION 1: TIME-STRATIFIED MODEL
# (SIMPLE INDICATOR VARIABLES)
data$ozone10 <- data$ozone/10
data$month <- as.factor(months(data$date,abbr=TRUE))
data$year <- as.factor(substr(data$date,1,4))
model1 <- glm(numdeaths ~ month/year,data,family=quasipoisson)
summary(model1)
pred1 <- predict(model1,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Time-stratified model (month strata)",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred1,lwd=2)
- 图 2 a 说明了应用到伦敦数据的这种日历月分层模型预测的死亡人数。
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model1)
Call:
glm(formula = numdeaths ~ month/year, family = quasipoisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.8334 -0.7629 -0.0403 0.7076 8.1611
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.041342 0.016999 296.562 < 2e-16 ***
month11月 -0.003091 0.024259 -0.127 0.898615
month12月 0.121045 0.023345 5.185 2.41e-07 ***
month1月 0.197499 0.022938 8.610 < 2e-16 ***
month2月 0.057217 0.024313 2.353 0.018714 *
month3月 0.066166 0.023653 2.797 0.005207 **
month4月 -0.004173 0.024266 -0.172 0.863489
month5月 -0.043040 0.024303 -1.771 0.076741 .
month6月 -0.045707 0.024526 -1.864 0.062545 .
month7月 -0.028773 0.024215 -1.188 0.234912
month8月 -0.090068 0.024601 -3.661 0.000258 ***
month9月 -0.057050 0.024599 -2.319 0.020497 *
month10月:year2003 0.001251 0.024033 0.052 0.958508
month11月:year2003 0.045016 0.024205 1.860 0.063085 .
month12月:year2003 -0.028108 0.022789 -1.233 0.217607
month1月:year2003 -0.059053 0.022109 -2.671 0.007631 **
month2月:year2003 0.055558 0.024248 2.291 0.022066 *
month3月:year2003 0.002729 0.023242 0.117 0.906543
month4月:year2003 0.045477 0.024215 1.878 0.060543 .
month5月:year2003 -0.005239 0.024596 -0.213 0.831347
month6月:year2003 -0.039573 0.025254 -1.567 0.117297
month7月:year2003 -0.068855 0.024820 -2.774 0.005592 **
month8月:year2003 0.152715 0.024241 6.300 3.75e-10 ***
month9月:year2003 -0.036478 0.025378 -1.437 0.150785
month10月:year2004 -0.088017 0.024587 -3.580 0.000353 ***
month11月:year2004 -0.050998 0.024794 -2.057 0.039846 *
month12月:year2004 -0.066660 0.023015 -2.896 0.003822 **
month1月:year2004 -0.063968 0.022137 -2.890 0.003904 **
month2月:year2004 -0.047157 0.024657 -1.913 0.055970 .
month3月:year2004 -0.069927 0.023676 -2.954 0.003183 **
month4月:year2004 -0.059746 0.024863 -2.403 0.016364 *
month5月:year2004 -0.052061 0.024890 -2.092 0.036609 *
month6月:year2004 -0.060681 0.025391 -2.390 0.016959 *
month7月:year2004 -0.108250 0.025076 -4.317 1.67e-05 ***
month8月:year2004 -0.082747 0.025685 -3.222 0.001298 **
month9月:year2004 -0.079758 0.025662 -3.108 0.001913 **
month10月:year2005 -0.140137 0.024928 -5.622 2.19e-08 ***
month11月:year2005 -0.112931 0.025197 -4.482 7.87e-06 ***
month12月:year2005 -0.119586 0.023336 -5.124 3.31e-07 ***
month1月:year2005 -0.095105 0.022317 -4.262 2.14e-05 ***
month2月:year2005 0.021358 0.024452 0.873 0.382536
month3月:year2005 0.022390 0.023129 0.968 0.333147
month4月:year2005 -0.044471 0.024766 -1.796 0.072717 .
month5月:year2005 -0.048398 0.024866 -1.946 0.051771 .
month6月:year2005 -0.107544 0.025703 -4.184 3.00e-05 ***
month7月:year2005 -0.135649 0.025259 -5.370 8.90e-08 ***
month8月:year2005 -0.092462 0.025750 -3.591 0.000339 ***
month9月:year2005 -0.138531 0.026062 -5.315 1.20e-07 ***
month10月:year2006 -0.182780 0.025217 -7.248 6.28e-13 ***
month11月:year2006 -0.116811 0.025223 -4.631 3.90e-06 ***
month12月:year2006 -0.198415 0.023838 -8.323 < 2e-16 ***
month1月:year2006 -0.205036 0.022986 -8.920 < 2e-16 ***
month2月:year2006 -0.026963 0.024750 -1.089 0.276115
month3月:year2006 -0.040432 0.023497 -1.721 0.085477 .
month4月:year2006 -0.085812 0.025032 -3.428 0.000622 ***
month5月:year2006 -0.105046 0.025235 -4.163 3.30e-05 ***
month6月:year2006 -0.089373 0.025581 -3.494 0.000488 ***
month7月:year2006 -0.095181 0.024990 -3.809 0.000144 ***
month8月:year2006 -0.106578 0.025845 -4.124 3.90e-05 ***
month9月:year2006 -0.160521 0.026217 -6.123 1.13e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.385637)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 2413.2 on 1766 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations:
- 优点: 易于理解,通常能很好地捕捉主要的长期模式。
- 缺点: 潜在的大量模型参数;隐含地假设相邻时间间隔之间的风险在生物学上不可信。
(二)Option 2:周期函数-傅里叶项 (Periodic functions-Fourier terms)
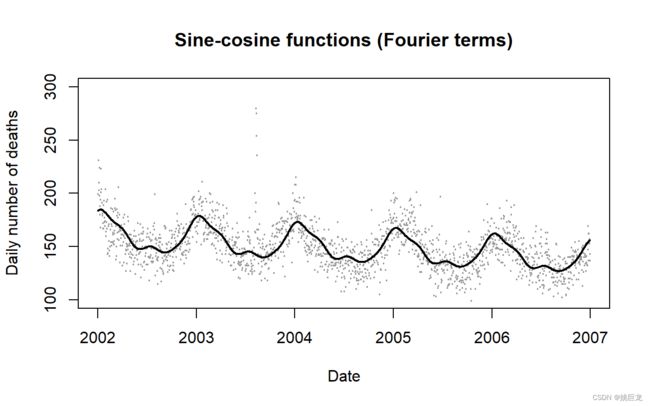
- 第二个方法是周期函数,通过在泊松模型中拟合傅里叶项,可以更平滑地对长期模式进行建模。这些是时间的正弦和余弦函数对,其基础周期反映了整个季节周期(即日历年),特别适合捕捉非常规则的季节模式。单个正弦/余弦对将结果中的季节性变化建模为每个日历年具有单个(等距)峰和谷的规则波(峰和谷的实际位置由数据指导)。但是,也可以引入谐波(具有更短波长的额外正弦/余弦对),从而产生更灵活的功能。
# OPTION 2: PERIODIC FUNCTIONS MODEL
# (FOURIER TERMS)
install.packages("tsModel")
library(tsModel)
data$time <- seq(nrow(data))
fourier <- harmonic(data$time,nfreq=4,period=365.25)
model2 <- glm(numdeaths ~ fourier + time,data,family=quasipoisson)
summary(model2)
pred2 <- predict(model2,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Sine-cosine functions (Fourier terms)",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred2,lwd=2)
- 图2b 说明了使用 4 个正弦/余弦对(1 个基波加 3 个谐波)来捕捉季节性,以及时间的线性函数来捕捉更广泛趋势随时间变化的伦敦数据的模型拟合。
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model2)
Call:
glm(formula = numdeaths ~ fourier + time, family = quasipoisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6295 -0.8413 -0.0802 0.7256 10.1819
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.084e+00 4.789e-03 1061.757 < 2e-16 ***
fourier1 4.651e-02 3.476e-03 13.381 < 2e-16 ***
fourier2 1.621e-02 3.432e-03 4.725 2.48e-06 ***
fourier3 -9.513e-03 3.418e-03 -2.783 0.00544 **
fourier4 5.716e-03 3.411e-03 1.675 0.09402 .
fourier5 9.059e-02 3.394e-03 26.689 < 2e-16 ***
fourier6 2.468e-02 3.407e-03 7.245 6.37e-13 ***
fourier7 3.686e-03 3.414e-03 1.080 0.28044
fourier8 9.364e-03 3.409e-03 2.747 0.00607 **
time -8.887e-05 4.648e-06 -19.118 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.581017)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 2776.8 on 1816 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 4
- 优点: 平滑地建模长期模式,使用相对较少的参数。
- 缺点: 比时间分层模型在数学上更复杂;模拟的季节模式总是被迫从一年到下一年保持相同,这可能无法很好地反映数据(例如,冬季死亡高峰的时间可能会有所不同)。仅傅立叶项无法捕捉长期的非季节性趋势(这可以通过添加日历时间的进一步函数来解决)。
(三)Option 3:灵活的样条函数 (Flexible spline functions)
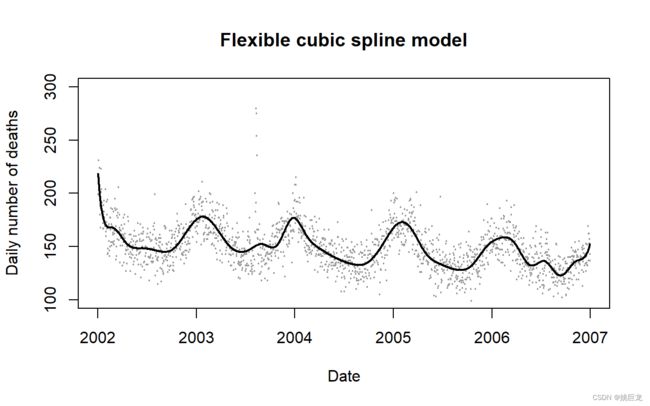
- 第三个方法是拟合时间的样条函数;这本质上是许多不同的多项式(最常见的是三次)曲线,它们端到端平滑地连接以覆盖整个周期。为了在实践中拟合样条函数,我们首先生成一组基变量,它们是主要时间变量的函数,然后将这些基变量包含在泊松模型中。
- 在生成样条基础时,有必要确定应该有多少个节点(连接点),这决定了将使用多少个端到端三次曲线,因此决定曲线的灵活度。节点太少无法密切捕捉主要的长期模式,节点太多会导致函数非常“不稳定”,它可能与感兴趣的变量竞争来解释感兴趣的短期变化,扩大相对风险估计的置信区间。样条函数的灵活性有时以自由度数而不是节点数为框架,其中更多的自由度对应于更多的节点,并且两者都意味着更灵活的函数。
# OPTION 3: SPLINE MODEL
# (FLEXIBLE SPLINE FUNCTIONS)
library(splines)
spl <- bs(data$time,degree=3,df=35)
model3 <- glm(numdeaths ~ spl,data,family=quasipoisson)
summary(model3)
pred3 <- predict(model3,type="response")
plot(data$date,data$numdeaths,ylim=c(100,300),pch=19,cex=0.2,col=grey(0.6),
main="Flexible cubic spline model",ylab="Daily number of deaths",
xlab="Date")
lines(data$date,pred3,lwd=2)
- 图 2c 是应用于伦敦数据集的样条函数,该函数使用 节点数为 34 节 [= (日历年数 x 7) – 1],这是每日死亡率数据的常见选择。尽管对于多少个节点是最佳的尚无共识,但每年 7 个节点已被证明是在为季节性提供充分控制和其他时间趋势混淆之间的平衡,同时留下足够的信息来估计暴露效应)。
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model3)
Call:
glm(formula = numdeaths ~ spl, family = quasipoisson, data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6791 -0.7950 -0.0407 0.7092 9.3852
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.38737 0.03486 154.541 < 2e-16 ***
spl1 -0.31076 0.06697 -4.640 3.73e-06 ***
spl2 -0.20888 0.04387 -4.762 2.08e-06 ***
spl3 -0.40118 0.05166 -7.766 1.35e-14 ***
spl4 -0.37987 0.04382 -8.670 < 2e-16 ***
spl5 -0.40692 0.04704 -8.650 < 2e-16 ***
spl6 -0.42251 0.04485 -9.421 < 2e-16 ***
spl7 -0.27138 0.04512 -6.015 2.18e-09 ***
spl8 -0.17365 0.04419 -3.930 8.83e-05 ***
spl9 -0.26489 0.04483 -5.909 4.11e-09 ***
spl10 -0.41225 0.04535 -9.091 < 2e-16 ***
spl11 -0.41962 0.04562 -9.199 < 2e-16 ***
spl12 -0.32815 0.04537 -7.232 7.01e-13 ***
spl13 -0.43933 0.04523 -9.712 < 2e-16 ***
spl14 -0.12734 0.04457 -2.857 0.00432 **
spl15 -0.33645 0.04501 -7.474 1.21e-13 ***
spl16 -0.39864 0.04565 -8.733 < 2e-16 ***
spl17 -0.45648 0.04615 -9.891 < 2e-16 ***
spl18 -0.49703 0.04644 -10.702 < 2e-16 ***
spl19 -0.51027 0.04630 -11.022 < 2e-16 ***
spl20 -0.38345 0.04551 -8.425 < 2e-16 ***
spl21 -0.21867 0.04478 -4.883 1.14e-06 ***
spl22 -0.23762 0.04491 -5.291 1.36e-07 ***
spl23 -0.44907 0.04582 -9.802 < 2e-16 ***
spl24 -0.49518 0.04650 -10.649 < 2e-16 ***
spl25 -0.54217 0.04681 -11.582 < 2e-16 ***
spl26 -0.53737 0.04656 -11.542 < 2e-16 ***
spl27 -0.36096 0.04575 -7.889 5.25e-15 ***
spl28 -0.31603 0.04537 -6.966 4.57e-12 ***
spl29 -0.31964 0.04567 -6.999 3.63e-12 ***
spl30 -0.57260 0.04664 -12.276 < 2e-16 ***
spl31 -0.40232 0.04730 -8.506 < 2e-16 ***
spl32 -0.66102 0.04968 -13.306 < 2e-16 ***
spl33 -0.42073 0.05637 -7.464 1.31e-13 ***
spl34 -0.48379 0.05801 -8.340 < 2e-16 ***
spl35 -0.36101 0.05369 -6.724 2.38e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.432375)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 2499.7 on 1790 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 4
- 优点: 平滑地模拟长期模式;可以以允许从一年到下一年变化的方式捕捉季节性模式;并且还将捕捉数据中的长期非季节性趋势。
- 缺点: 比其他方法在数学上更复杂(尽管主要统计软件包中提供了生成样条基的函数)。
(四)围绕长期模式的残余变化
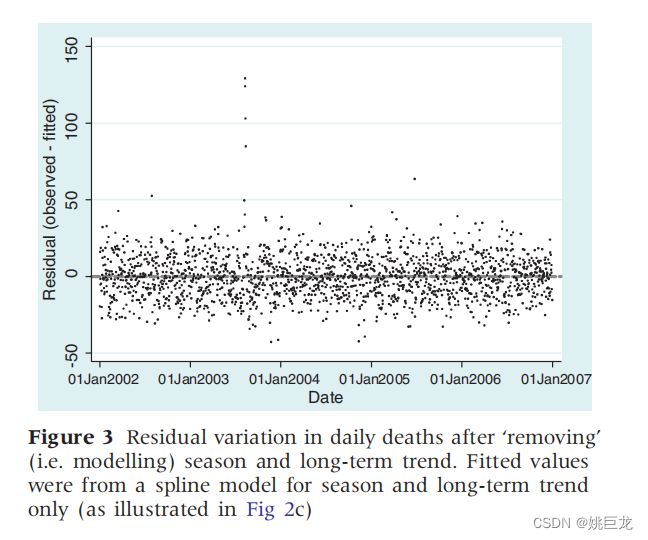
- Residual variation around the long-term pattern
- 如果使用上述方法之一控制季节性和长期趋势,我们将留下长期模式不再明显的残余变化(图 3)。通过向该模型添加感兴趣的风险敞口,我们现在可以解决我们的主要目标,即调查围绕长期模式的剩余短期变化是否部分由风险敞口变量解释。
# PLOT RESPONSE RESIDUALS OVER TIME
# FROM MODEL 3
res3 <- residuals(model3,type="response")
plot(data$date,res3,ylim=c(-50,150),pch=19,cex=0.4,col=grey(0.6),
main="Residuals over time",ylab="Residuals (observed-fitted)",xlab="Date")
abline(h=1,lty=2,lwd=2)
五、暴露结果关联和混杂
1. 臭氧
在伦敦的数据中,拟合死亡率的朴素泊松模型,臭氧作为唯一的解释变量,没有对季节性或长期趋势进行调整,表明臭氧水平每增加 10 µg/m 3与死亡风险比为0.991 (95% CI 0.987 to 0.994, P < 0.001),即较高的臭氧与较低的死亡风险相关。
# ESTIMATING OZONE-MORTALITY ASSOCIATION
# (CONTROLLING FOR CONFOUNDERS)
install.packages("Epi")
library(Epi)
# UNADJUSTED MODEL
model4 <- glm(numdeaths ~ ozone10,data,family=quasipoisson)
summary(model4)
(eff4 <- ci.lin(model4,subset="ozone10",Exp=T))
# CONTROLLING FOR SEASONALITY (WITH SPLINE AS IN MODEL 3)
model5 <- update(model4,.~.+spl)
summary(model5)
(eff5 <- ci.lin(model5,subset="ozone10",Exp=T))
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model4)
Call:
glm(formula = numdeaths ~ ozone10, family = quasipoisson, data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-4.6058 -1.1692 -0.1195 1.0252 10.2613
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.039768 0.006887 731.820 < 2e-16 ***
ozone10 -0.009364 0.001766 -5.301 1.29e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 2.831608)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 5049.8 on 1824 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 4
> (eff4 <- ci.lin(model4,subset="ozone10",Exp=T))
Estimate StdErr z P exp(Est.) 2.5% 97.5%
ozone10 -0.009363689 0.001766441 -5.300877 1.152477e-07 0.99068 0.987256 0.9941159
但我们知道,至少部分原因很可能是由季节混淆来解释的。在模型中添加季节和长期趋势调整后(使用上述选项 3 中的灵活样条),估计效果的方向反转(RR 每 10 µg/m 3= 1.007,95% CI 1.003 至 1.010,p < 0.001;或等效地,风险增加 0.7% [0.3–1.0])。
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model5)
Call:
glm(formula = numdeaths ~ ozone10 + spl, family = quasipoisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.7422 -0.7971 -0.0281 0.7157 8.9675
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.394524 0.034628 155.785 < 2e-16 ***
ozone10 0.006608 0.001599 4.133 3.74e-05 ***
spl1 -0.357002 0.067365 -5.300 1.30e-07 ***
spl2 -0.227264 0.043818 -5.187 2.38e-07 ***
spl3 -0.448092 0.052521 -8.532 < 2e-16 ***
spl4 -0.413019 0.044239 -9.336 < 2e-16 ***
spl5 -0.435182 0.047200 -9.220 < 2e-16 ***
spl6 -0.446916 0.044926 -9.948 < 2e-16 ***
spl7 -0.286102 0.044935 -6.367 2.44e-10 ***
spl8 -0.199243 0.044294 -4.498 7.29e-06 ***
spl9 -0.289330 0.044890 -6.445 1.48e-10 ***
spl10 -0.461361 0.046559 -9.909 < 2e-16 ***
spl11 -0.458090 0.046242 -9.906 < 2e-16 ***
spl12 -0.368889 0.046122 -7.998 2.25e-15 ***
spl13 -0.452845 0.045018 -10.059 < 2e-16 ***
spl14 -0.151914 0.044647 -3.403 0.000682 ***
spl15 -0.362700 0.045142 -8.035 1.69e-15 ***
spl16 -0.434286 0.046127 -9.415 < 2e-16 ***
spl17 -0.490948 0.046560 -10.545 < 2e-16 ***
spl18 -0.531890 0.046871 -11.348 < 2e-16 ***
spl19 -0.546444 0.046798 -11.677 < 2e-16 ***
spl20 -0.389140 0.045204 -8.609 < 2e-16 ***
spl21 -0.253212 0.045219 -5.600 2.48e-08 ***
spl22 -0.259292 0.044872 -5.778 8.88e-09 ***
spl23 -0.491057 0.046595 -10.539 < 2e-16 ***
spl24 -0.536585 0.047235 -11.360 < 2e-16 ***
spl25 -0.567940 0.046889 -12.112 < 2e-16 ***
spl26 -0.566718 0.046770 -12.117 < 2e-16 ***
spl27 -0.375020 0.045558 -8.232 3.52e-16 ***
spl28 -0.336118 0.045306 -7.419 1.82e-13 ***
spl29 -0.366222 0.046707 -7.841 7.63e-15 ***
spl30 -0.606314 0.047016 -12.896 < 2e-16 ***
spl31 -0.456894 0.048773 -9.368 < 2e-16 ***
spl32 -0.679548 0.049512 -13.725 < 2e-16 ***
spl33 -0.447328 0.056359 -7.937 3.62e-15 ***
spl34 -0.512691 0.057949 -8.847 < 2e-16 ***
spl35 -0.383634 0.053517 -7.169 1.10e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.414007)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 2475.5 on 1789 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 4
> (eff5 <- ci.lin(model5,subset="ozone10",Exp=T))
Estimate StdErr z P exp(Est.) 2.5% 97.5%
ozone10 0.006608467 0.001598843 4.133281 3.576213e-05 1.00663 1.003481 1.00979
这表明在短期内,较高的臭氧与较高的死亡风险相关。像这样的小效应量在环境流行病学中相对普遍,但如果整个人群都受到暴露,小效应通常仍然具有公共卫生重要性。
2. 其他时变因素的混淆
在仅针对季节和长期趋势进行调整的分析中,臭氧似乎与死亡率呈正相关。但会不会有其他因素的混淆?
在一般流行病学中,常见的混杂因素包括年龄、性别、体重指数、吸烟状况、饮酒等,但这些“标准混杂因素”不适用于该伦敦数据集,因为在人群水平上,这些因素的分布不太可能每天都在变化,并且不能与环境暴露的波动(例如污染水平)相关联。
分析单位是由单行数据(在我们的例子中是天)而不是个人表示的时间间隔。因此,潜在的混杂因素应该是可以每天变化的变量,这似乎与我们感兴趣的暴露(臭氧)以及结果(死亡率)的日常波动有关。在这个例子中,一个明显的候选者是环境温度,因为温度每天都在变化,臭氧水平与温度有关(由于阳光参与臭氧的产生,臭氧在炎热的日子里往往更高),它是众所周知,温度与短期内的死亡风险有关。
# CONTROLLING FOR TEMPERATURE
# (TEMPERATURE MODELLED WITH CATEGORICAL VARIABLES FOR DECILES)
cutoffs <- quantile(data$temperature,probs=0:10/10)
tempdecile <- cut(data$temperature,breaks=cutoffs,include.lowest=TRUE)
model6 <- update(model5,.~.+tempdecile)
summary(model6)
(eff6 <- ci.lin(model6,subset="ozone10",Exp=T))
将当前温度添加到模型中(允许预期的非线性4)确实将估计的臭氧死亡率关联移向零,并且调整后的效果不再具有统计学意义(每 10 µg/m 3调整后的死亡风险比为 1.003, 95% CI 0.999–1.006,P = 0.11)。这表明,最初估计的当前臭氧水平与死亡风险之间的正相关关系在很大程度上可以通过温度混淆来解释。
——————————————————————————————【运行结果】——————————————————————————————————
> summary(model6)
Call:
glm(formula = numdeaths ~ ozone10 + spl + tempdecile, family = quasipoisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.4749 -0.7592 -0.0325 0.6998 8.6310
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.397434 0.033885 159.289 < 2e-16 ***
ozone10 0.002660 0.001650 1.613 0.106982
spl1 -0.355647 0.066453 -5.352 9.83e-08 ***
spl2 -0.215023 0.042925 -5.009 6.01e-07 ***
spl3 -0.449535 0.052067 -8.634 < 2e-16 ***
spl4 -0.416087 0.045145 -9.217 < 2e-16 ***
spl5 -0.516694 0.049237 -10.494 < 2e-16 ***
spl6 -0.437726 0.045604 -9.598 < 2e-16 ***
spl7 -0.299331 0.044730 -6.692 2.94e-11 ***
spl8 -0.185173 0.043329 -4.274 2.02e-05 ***
spl9 -0.289821 0.044665 -6.489 1.12e-10 ***
spl10 -0.443079 0.046972 -9.433 < 2e-16 ***
spl11 -0.550633 0.048016 -11.468 < 2e-16 ***
spl12 -0.412416 0.047248 -8.729 < 2e-16 ***
spl13 -0.443119 0.044840 -9.882 < 2e-16 ***
spl14 -0.153709 0.043806 -3.509 0.000461 ***
spl15 -0.349490 0.044111 -7.923 4.05e-15 ***
spl16 -0.434906 0.045638 -9.530 < 2e-16 ***
spl17 -0.492358 0.047545 -10.356 < 2e-16 ***
spl18 -0.632479 0.048350 -13.081 < 2e-16 ***
spl19 -0.554391 0.047527 -11.665 < 2e-16 ***
spl20 -0.399647 0.044679 -8.945 < 2e-16 ***
spl21 -0.236988 0.044409 -5.336 1.07e-07 ***
spl22 -0.260740 0.043819 -5.950 3.21e-09 ***
spl23 -0.477714 0.046766 -10.215 < 2e-16 ***
spl24 -0.594973 0.048102 -12.369 < 2e-16 ***
spl25 -0.628064 0.048007 -13.083 < 2e-16 ***
spl26 -0.580350 0.047597 -12.193 < 2e-16 ***
spl27 -0.368372 0.044714 -8.238 3.34e-16 ***
spl28 -0.332371 0.044260 -7.510 9.33e-14 ***
spl29 -0.349631 0.045895 -7.618 4.16e-14 ***
spl30 -0.618523 0.048199 -12.833 < 2e-16 ***
spl31 -0.549227 0.049455 -11.106 < 2e-16 ***
spl32 -0.712232 0.051275 -13.891 < 2e-16 ***
spl33 -0.454224 0.055707 -8.154 6.58e-16 ***
spl34 -0.503764 0.057161 -8.813 < 2e-16 ***
spl35 -0.379877 0.052373 -7.253 6.04e-13 ***
tempdecile(4,6.44] 0.001244 0.009769 0.127 0.898711
tempdecile(6.44,8.27] -0.010651 0.010343 -1.030 0.303273
tempdecile(8.27,10] 0.015512 0.010701 1.450 0.147340
tempdecile(10,11.5] 0.018312 0.011711 1.564 0.118059
tempdecile(11.5,13.3] 0.013201 0.012743 1.036 0.300404
tempdecile(13.3,15.3] 0.027105 0.014409 1.881 0.060116 .
tempdecile(15.3,17] 0.034276 0.015695 2.184 0.029104 *
tempdecile(17,18.9] 0.038294 0.016604 2.306 0.021208 *
tempdecile(18.9,28.2] 0.119680 0.017702 6.761 1.85e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.345358)
Null deviance: 5129.6 on 1825 degrees of freedom
Residual deviance: 2351.7 on 1780 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 4
> (eff6 <- ci.lin(model6,subset="ozone10",Exp=T))
Estimate StdErr z P exp(Est.) 2.5% 97.5%
ozone10 0.002660343 0.001649596 1.612724 0.1068044 1.002664 0.9994274 1.005911
汇总一下:
> # BUILD A SUMMARY TABLE WITH EFFECT AS PERCENT INCREASE
> tabeff <- rbind(eff4,eff5,eff6)[,5:7]
> tabeff <- (tabeff-1)*100
> dimnames(tabeff) <- list(c("Unadjusted","Plus season/trend","Plus temperature"),
+ c("RR","ci.low","ci.hi"))
> round(tabeff,2)
RR ci.low ci.hi
Unadjusted -0.93 -1.27 -0.59
Plus season/trend 0.66 0.35 0.98
Plus temperature 0.27 -0.06 0.59
六、允许延迟曝光效果
(一)单滞后模型 (SINGLE-LAG MODELS)
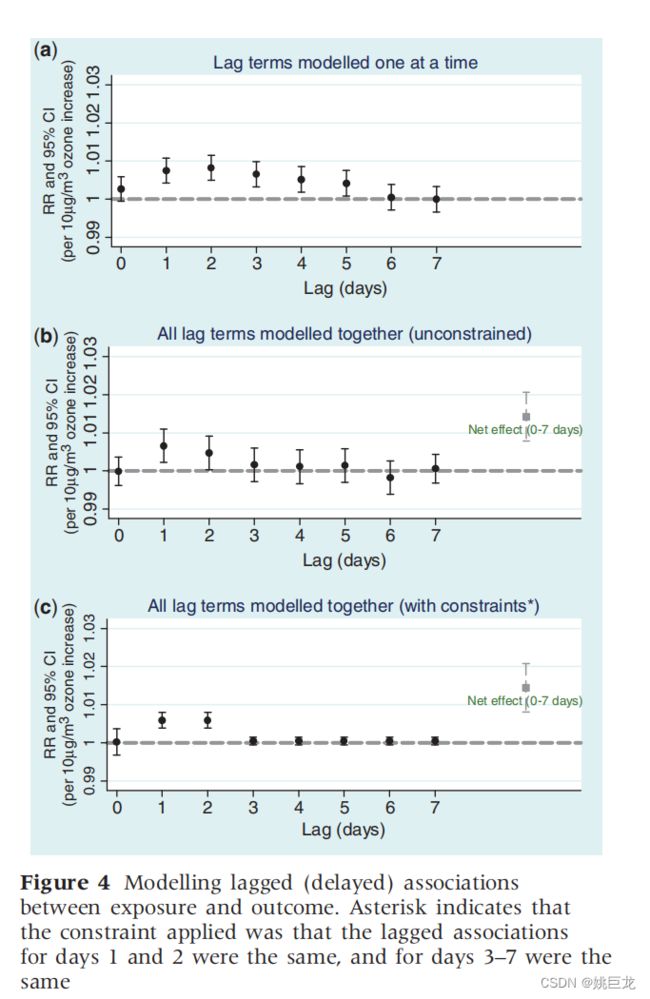
在伦敦的数据中,到目前为止,我们的模型已将特定日期的死亡率与同一天的臭氧水平相关联。但是,暴露与结果之间可能存在延迟(或“滞后”)关联。昨天的臭氧水平可能比今天的臭氧水平更能预测今天的死亡风险。估计昨天的臭氧水平和今天的死亡风险之间的关联(即滞后 1 天的关联)只是将臭氧序列及时向前移动(即向下一行)并重新拟合之前的模型的问题。图 4a 显示了当我们将滞后时间从 0 天增加到 7 天时,估计的臭氧死亡率关联(根据温度调整)如何变化。
# EXPLORING THE LAGGED (DELAYED) EFFECTS
# SINGLE-LAG MODELS
# PREPARE THE TABLE WITH ESTIMATES
tablag <- matrix(NA,7+1,3,dimnames=list(paste("Lag",0:7),
c("RR","ci.low","ci.hi")))
# RUN THE LOOP
for(i in 0:7) {
# LAG OZONE AND TEMPERATURE VARIABLES
ozone10lag <- Lag(data$ozone10,i)
tempdecilelag <- cut(Lag(data$temperature,i),breaks=cutoffs,
include.lowest=TRUE)
# DEFINE THE TRANSFORMATION FOR TEMPERATURE
# LAG SAME AS ABOVE, BUT WITH STRATA TERMS INSTEAD THAN LINEAR
mod <- glm(numdeaths ~ ozone10lag + tempdecilelag + spl,data,
family=quasipoisson)
tablag[i+1,] <- ci.lin(mod,subset="ozone10lag",Exp=T)[5:7]
}
tablag
——————————————————————————————【运行结果】——————————————————————————————————
> tablag
RR ci.low ci.hi
Lag 0 1.002664 0.9994274 1.005911
Lag 1 1.007482 1.0042176 1.010756
Lag 2 1.008195 1.0049222 1.011479
Lag 3 1.006503 1.0032115 1.009805
Lag 4 1.005188 1.0018610 1.008527
Lag 5 1.004218 1.0008532 1.007594
Lag 6 1.000517 0.9971563 1.003890
Lag 7 1.000013 0.9966491 1.003389
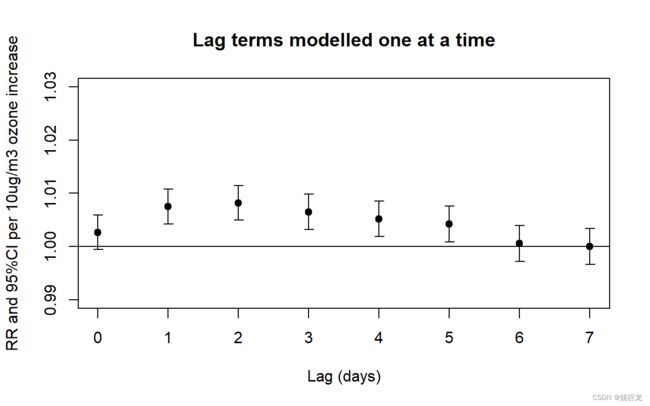
当滞后时间在 1 到 5 天之间时,有证据表明臭氧与死亡率之间存在关联。但是,这些不同的滞后效应不会相互调整;到目前为止,每个滞后都已一次安装在模型中。
plot(0:7,0:7,type="n",ylim=c(0.99,1.03),main="Lag terms modelled one at a time",
xlab="Lag (days)",ylab="RR and 95%CI per 10ug/m3 ozone increase")
abline(h=1)
arrows(0:7,tablag[,2],0:7,tablag[,3],length=0.05,angle=90,code=3)
points(0:7,tablag[,1],pch=19)
(二)分布滞后模型 (UNCONSTRAINED DLM)
为了解决这个问题,可以在模型中同时输入所有滞后变量(0 到 7 天移位系列)。这被称为 “分布式滞后模型” ,并应用于伦敦数据,得出图 4中显示的效果估计值。与单个滞后模型相比,滞后天 0 到 5 的所有效应估计值现在都趋于零,这表明(如预期的那样)估计的单个滞后效应相互混淆。在滞后第 1 天和第 2 天仍有独立的臭氧死亡率关联的证据,表明当天的死亡风险与前 2 天的臭氧水平正相关(或者,等效地,当前臭氧与以下天的死亡率正相关2天)。
library(dlnm)
cbo3unc <- crossbasis(data$ozone,lag=c(0,7),argvar=list(type="lin",cen=FALSE),
arglag=list(type="integer"))
summary(cbo3unc)
cbtempunc <- crossbasis(data$temperature,lag=c(0,7),
argvar=list(type="strata",knots=cutoffs[2:10]),
arglag=list(type="integer"))
summary(cbtempunc)
model7 <- glm(numdeaths ~ cbo3unc + cbtempunc + spl,data,family=quasipoisson)
pred7 <- crosspred(cbo3unc,model7,at=10)
tablag2 <- with(pred7,t(rbind(matRRfit,matRRlow,matRRhigh)))
colnames(tablag2) <- c("RR","ci.low","ci.hi")
tablag2
pred7$allRRfit ; pred7$allRRlow ; pred7$allRRhigh
——————————————————————————————【运行结果】——————————————————————————————————
> summary(cbo3unc)
CROSSBASIS FUNCTIONS
observations: 1826
range: 1.181818 to 119.2457
lag period: 0 7
total df: 8
BASIS FOR VAR:
fun: lin
intercept: FALSE
BASIS FOR LAG:
fun: integer
values: 0 1 2 3 4 5 6 ...
intercept: TRUE
> summary(cbtempunc)
CROSSBASIS FUNCTIONS
observations: 1826
range: -1.400507 to 28.175
lag period: 0 7
total df: 72
BASIS FOR VAR:
fun: strata
df: 9
breaks: 4.003125 6.44375 8.271222 10.01869 11.47275 13.34375 15.27115 ...
ref: 1
intercept: FALSE
BASIS FOR LAG:
fun: integer
values: 0 1 2 3 4 5 6 ...
intercept: TRUE
> tablag2
RR ci.low ci.hi
lag0 0.9998301 0.9961204 1.003554
lag1 1.0066534 1.0022830 1.011043
lag2 1.0046525 1.0002397 1.009085
lag3 1.0015800 0.9971671 1.006012
lag4 1.0011224 0.9967088 1.005555
lag5 1.0014855 0.9970741 1.005916
lag6 0.9982712 0.9939150 1.002647
lag7 1.0007098 0.9969463 1.004488
> pred7$allRRfit ; pred7$allRRlow ; pred7$allRRhigh
10
1.01437
10
1.007994
10
1.020786
plot(pred7,var=10,type="p",ci="bars",col=1,pch=19,ylim=c(0.99,1.03),
main="All lag terms modelled together (unconstrained)",xlab="Lag (days)",
ylab="RR and 95%CI per 10ug/m3 ozone increase")
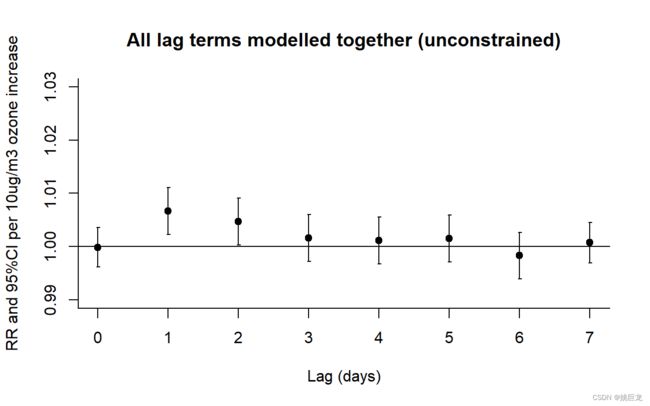
简单的“无约束”分布式滞后模型的缺点是滞后项可能高度相关,并且模型中的共线性可能导致不精确的估计(宽置信区间)。
(三)受约束的分布滞后模型 (CONSTRAINED (LAG-STRATIFIED) DLM)
可以通过对不同滞后的效果估计施加一些约束来克服上述问题(“受约束的分布式滞后模型”)。
cbo3constr <- crossbasis(data$ozone,lag=c(0,7),argvar=list(type="lin",cen=FALSE),
arglag=list(type="strata",knots=c(1,3)))
summary(cbo3constr)
model8 <- glm(numdeaths ~ cbo3constr + cbtempunc + spl,data,family=quasipoisson)
pred8 <- crosspred(cbo3constr,model8,at=10)
tablag3 <- with(pred8,t(rbind(matRRfit,matRRlow,matRRhigh)))
colnames(tablag3) <- c("RR","ci.low","ci.hi")
tablag3
pred8$allRRfit ; pred8$allRRlow ; pred8$allRRhigh
——————————————————————————————【运行结果】——————————————————————————————————
> summary(cbo3constr)
CROSSBASIS FUNCTIONS
observations: 1826
range: 1.181818 to 119.2457
lag period: 0 7
total df: 3
BASIS FOR VAR:
fun: lin
intercept: FALSE
BASIS FOR LAG:
fun: strata
df: 3
breaks: 1 3
ref: 1
intercept: TRUE
> tablag3
RR ci.low ci.hi
lag0 1.000159 0.9967305 1.003599
lag1 1.005880 1.0038254 1.007938
lag2 1.005880 1.0038254 1.007938
lag3 1.000516 0.9994934 1.001540
lag4 1.000516 0.9994934 1.001540
lag5 1.000516 0.9994934 1.001540
lag6 1.000516 0.9994934 1.001540
lag7 1.000516 0.9994934 1.001540
> pred8$allRRfit ; pred8$allRRlow ; pred8$allRRhigh
10
1.01457
10
1.00827
10
1.02091
图4c 显示了对分布式滞后模型施加简单约束的结果,即第 1 天和第 2 天的效果估计值相同,第 3 到第 7 天(含)的效果估计值相同(所谓的’滞后分层的’分布式滞后模型,这可能是由图 4的无约束模型中揭示的广泛模式所证明的乙)。
plot(pred8,var=10,type="p",ci="bars",col=1,pch=19,ylim=c(0.99,1.03),
main="All lag terms modelled together (with costraints)",xlab="Lag (days)",
ylab="RR and 95%CI per 10ug/m3 ozone increase")
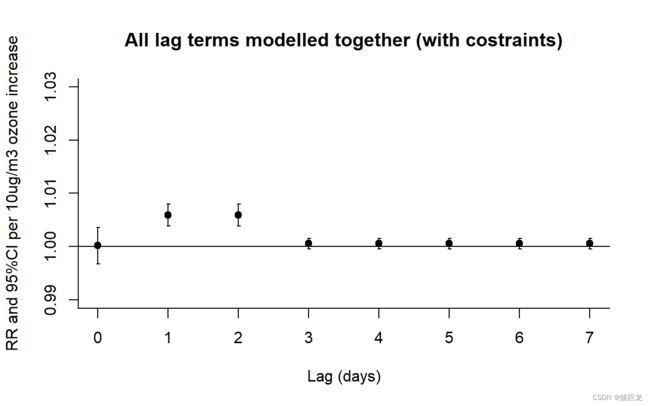
共线性现在大大减少,需要估计的参数更少,并且可以更精确地估计单个滞后的关联,尽管对这种方法的潜在批评是,如果没有预先指定约束的选择,可能会被认为太“数据驱动”。可以应用更复杂的约束,包括滞后时间的平滑(多项式或样条)函数。
(四)Short-term displacement, or ‘harvesting’
分布式滞后模型有时会显示出一个明显奇怪的特征:短期滞后时风险比升高,而较长滞后时明显具有保护作用。 例如,一项将环境温度与心脏病住院人数联系起来的研究发现,在气温非常高的日子里,住院人数增加了,但在高温事件发生几天后,住院人数比预期的要少。
这表明在任何情况下因心脏病入院几天内的高度脆弱的人可能只是由于高温事件而将他们的心脏问题提前了几天。这是一种被称为短期流离失所或“收获”的现象。如果似乎存在收获,则可以通过考虑在整个滞后期内暴露与结果之间的累积关联来确定短期风险增加被较长滞后风险降低“抵消”的程度(通过求和模型系数,如前所述)。
七、模型检查和敏感性分析
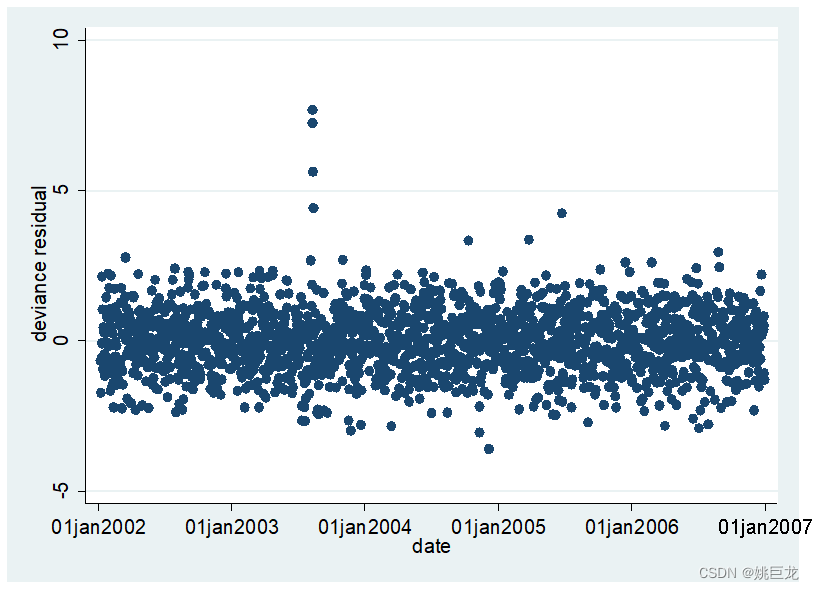
开发了一个或多个模型后,在展示之前,必须检查残差图并进行敏感性分析,以揭示模型假设、数据异常、残差自相关或主要结果对决策的敏感性的任何问题已经做出来了。补充附录中描述了基于偏差残差的有用诊断图(可从IJE online上的补充数据)和其他论文提供了更多详细信息。
# MODEL CHECKING
res7 <- residuals(model7,type="deviance")
plot(data$date,res7,ylim=c(-5,10),pch=19,cex=0.7,col=grey(0.6),
main="Residuals over time",ylab="Deviance residuals",xlab="Date")
abline(h=0,lty=2,lwd=2)
此外,由于我们概述的建模过程涉及许多决策,我们建议进行多重敏感性分析,以检查主要结论对这些决策的变化是否稳健。敏感性分析可能包括改变模型中季节性和长期趋势的控制量(例如,通过改变基于样条的方法中的节点数,或傅里叶项方法中的谐波);以不同的方式指定暴露和混杂变量(例如,在伦敦分析中,我们可能会尝试将相对湿度作为线性变量而不是分类变量,或者调整为最大值而不是每日平均温度);改变模型中包含滞后效应的方式;并更改其他关键的特定于上下文的决策。
pacf(res7,na.action=na.omit,main="From original model")
model9 <- update(model7,.~.+Lag(res7,1))
pacf(residuals(model9,type="deviance"),na.action=na.omit,
main="From model adjusted for residual autocorrelation")
自相关(ACF)和偏自相关(PACF)图:
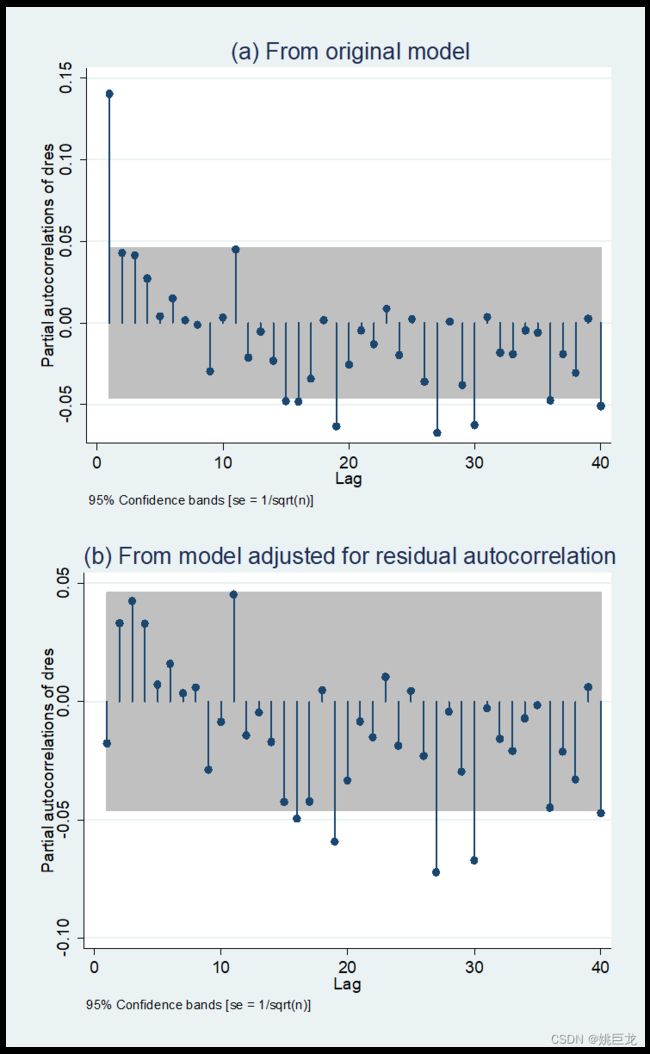
一种具有异方差性的非平稳序列的自相关函数图和偏自相关函数图。
(由图可知,对于具有异方差性的非平稳序列,其各阶自相关函数值显著不为 0,且呈现出正负交错,缓慢下降的趋势;偏自相关函数值也呈正负交错的形式,但下降趋势明显。)
八、思维导图总结
参考文献
Krishnan Bhaskaran, Antonio Gasparrini, Shakoor Hajat, Liam Smeeth, Ben Armstrong, Time series regression studies in environmental epidemiology, International Journal of Epidemiology, Volume 42, Issue 4, August 2013, Pages 1187–1195, https://doi.org/10.1093/ije/dyt092