【python+ROS+路径规划】六、mpc轨迹规划和跟踪

所使用的就是pyomo,使用mpc框架，达到的效果是优化轨迹并进行轨迹跟踪，如图：
pyomo相关教程：【python+ROS+路径规划】五、pyomo非线性规划工具.

使用mpc优化路径

首先要有一个初始路径：
使用Astar的可以见这篇文章：【python+ROS+路径规划】四、发布路径
或者也可以使用ros包中的路径。

mpc框架的数学形式

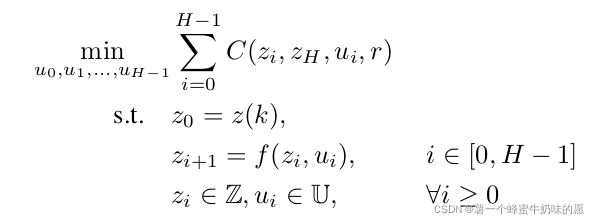
其中目标函数为：

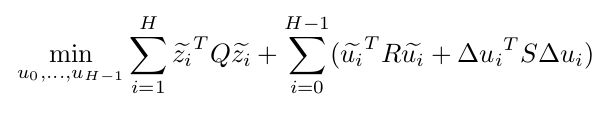
这里为了简化模型，控制不是加速度而是速度，第一项是原始轨迹和优化轨迹的差，第二项是参考控制和优化控制的差，第三项是两个相邻的控制之间的差。

mpc轨迹规划代码

使用pyomo搭建的具体框架如下：

def MPC_opt(path,theta):
	#滚动长度
    H = len(path)-1
    model = ConcreteModel()
    #Set
    model.zk_number = RangeSet(1,H)
    model.uk_number = RangeSet(0,H)
    model.uk_obj = RangeSet(0,H-1)

    # Parameters
    #需要调节的参数如下
    model.Q = Param(RangeSet(1,2),initialize={1:1,2:1},mutable=True)
    model.R = Param(RangeSet(1,2),initialize={1:1,2:1},mutable=True)
    model.S = Param(RangeSet(1,2),initialize={1:1,2:1},mutable=True)
	#这个要根据机器人来定
    model.vmax = Param(initialize=0.5)
	#这个也要自己计算，这里是每两个点之间的距离除以最大速度
    model.dt = Param(initialize=0.04998/model.vmax)
   

    model.z0 = Param(RangeSet(0,state_number-1),initialize={0:path[0][0],1:path[0][1],2:theta[0]})



    # Variables

    model.z = Var(RangeSet(0,state_number-1),model.uk_number)   #建立[x,y,θ]变量
    model.v = Var(model.uk_number,bounds=(0,model.vmax))
    model.w = Var(model.uk_number,bounds=(-1,1))

    #0:x   1:y    2：θ
    #0:v   1:w

    # Constraint
    model.z0_update = Constraint(RangeSet(0,state_number-1),rule=lambda model,i:model.z[i,0]==model.z0[i])
    
    model.x_update = Constraint(model.uk_number,rule=lambda model,k:model.z[0,k+1]==model.z[0,k]+model.v[k]*cos(model.z[2,k])*model.dt
                                if k<=H-1 else Constraint.Skip)
    model.y_update = Constraint(model.uk_number,rule=lambda model,k:model.z[1,k+1]==model.z[1,k]+model.v[k]*sin(model.z[2,k])*model.dt
                                if k<=H-1 else Constraint.Skip)
    model.θ_update = Constraint(model.uk_number,rule=lambda model,k:model.z[2,k+1]==model.z[2,k]+model.w[k]*model.dt
                                if k<=H-1 else Constraint.Skip)
    

    

    

    # Objective
    model.xQx = model.Q[1]*sum((model.z[0,i]-path[i-1][0])**2 for i in model.zk_number)
    model.yQy = model.Q[2]*sum((model.z[1,i]-path[i-1][1])**2 for i in model.zk_number)


    model.vRv = model.R[1]*sum((model.vmax-model.v[i])**2 for i in model.uk_obj)
    model.wRw = model.R[2]*sum(model.w[i]**2 for i in model.uk_obj)

    model.dvSdv = model.S[1]*sum((model.v[i+1]-model.v[i])**2 for i in model.uk_obj)
    model.dwSdw = model.S[2]*sum((model.w[i+1]-model.w[i])**2 for i in model.uk_obj)

    model.obj = Objective(expr=model.xQx+model.yQy+model.vRv+model.wRw+model.dvSdv+model.dwSdw,sense=minimize)
    

    #Solve
    SolverFactory("ipopt").solve(model)
    x_opt = [model.z[0,k]() for k in model.zk_number]
    y_opt = [model.z[1,k]() for k in model.zk_number]
    θ_opt = [model.z[2,k]() for k in model.zk_number]




    return x_opt,y_opt,θ_opt

这里注意，轨迹的优化方面初始是没有角度的，之所以最后给出了角度，是因为有运动学方程，这也是mpc的优点。

使用mpc跟踪

框架搭建同理：

def MPC_tracking(path,theta,vref,info):
    H = len(path)-1

    if H <= 2:
        return 0,0
    else:

        model = ConcreteModel()
        #Set
        model.zk_number = RangeSet(1,H)
        model.uk_number = RangeSet(0,H)
        model.uk_obj = RangeSet(0,H-1)

        # Parameters
        model.Q = Param(RangeSet(1,3),initialize={1:1,2:1,3:0.01},mutable=True)
        model.R = Param(RangeSet(1,2),initialize={1:0.5,2:0.02},mutable=True)
        model.S = Param(RangeSet(1,2),initialize={1:0.1,2:0.05},mutable=True)

        model.vref = vref

        model.dt = 0.04998/model.vref
    

        model.z0 = Param(RangeSet(0,state_number-1),initialize={0:info[0],1:info[1],2:info[2]})



        # Variables

        model.z = Var(RangeSet(0,state_number-1),model.uk_number)   #建立[x,y,θ]变量
        model.v = Var(model.uk_number,bounds=(0,vmax))
        model.w = Var(model.uk_number,bounds=(-1,1))

        #0:x   1:y    2:θ
        #0:v   1:w

        # Constraint
        model.z0_update = Constraint(RangeSet(0,state_number-1),rule=lambda model,i:model.z[i,0]==model.z0[i])
        
        model.x_update = Constraint(model.uk_number,rule=lambda model,k:model.z[0,k+1]==model.z[0,k]+model.v[k]*cos(model.z[2,k])*model.dt[k]
                                    if k<=H-1 else Constraint.Skip)
        model.y_update = Constraint(model.uk_number,rule=lambda model,k:model.z[1,k+1]==model.z[1,k]+model.v[k]*sin(model.z[2,k])*model.dt[k]
                                    if k<=H-1 else Constraint.Skip)
        model.θ_update = Constraint(model.uk_number,rule=lambda model,k:model.z[2,k+1]==model.z[2,k]+model.w[k]*model.dt[k]
                                    if k<=H-1 else Constraint.Skip)


        # Objective
        model.xQx = model.Q[1]*sum((model.z[0,i]-path[i-1][0])**2 for i in model.zk_number)
        model.yQy = model.Q[2]*sum((model.z[1,i]-path[i-1][1])**2 for i in model.zk_number)
        model.θQθ = model.Q[3]*sum((model.z[2,i]-theta[i])**2 for i in model.zk_number)


        model.vRv = model.R[1]*sum((model.vref[i]-model.v[i])**2 for i in model.uk_obj)
        model.wRw = model.R[2]*sum(model.w[i]**2 for i in model.uk_obj)

        model.dvSdv = model.S[1]*sum((model.v[i+1]-model.v[i])**2 for i in model.uk_obj)
        model.dwSdw = model.S[2]*sum((model.w[i+1]-model.w[i])**2 for i in model.uk_obj)

        model.obj = Objective(expr=model.xQx+model.yQy+model.θQθ+model.vRv+model.wRw+model.dvSdv+model.dwSdw,sense=minimize)
        

        #Solve
        SolverFactory("ipopt").solve(model)
        v_opt = model.v[0]()
        w_opt = model.w[0]() 

        return v_opt,w_opt

发布控制指令

之后发布速度和角速度：

    def mpcTracking(self):
        #前置信息
        #首先计算时间
        dt = 0.04998/self.Vref#最后一个没有用，第一个对应从第一个点到第二个点应该用的时间
        theta = self.iniTheta
        pose = self.iniPose
        vref = self.Vref
        #最后一个速度应该为0,先设置在约束上面

        MPCCC = rospy.Publisher("/cmd_vel",Twist,queue_size=15)
        msg = Twist()

        # rate = rospy.Rate(400)
        
        k = 0
        T = 10  #滚动时域
#----------------------------------------------------------------------------------
		while k < len(dt):
            du = rospy.Duration(dt[k])
        #需要根据时间获取当前信息
            now_x,now_y,now_theta = self.getNowPose()
        #这里得到的角度和使用的角度可能不一样
			info = [now_x,now_y,opt_theta]
#---------------------------------------------------------------------------------------
		#这里使用相关mpc算法，拿到速度角速度指令
		#v_opt,w_opt
#---------------------------------------------------------------------------------------
            msg.linear.x = v_opt
            msg.angular.z = w_opt
            MPCCC.publish(msg)
            # rate.sleep()
            rospy.sleep(du)
            k +=1