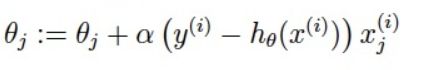机器学习基础:梯度下降原理及代码实现
梯度下降及代码实现
凸函数
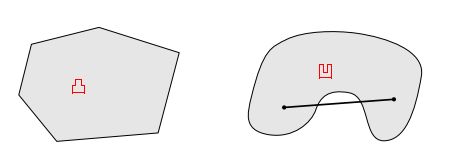
凸集:如果集合C中任意2个元素连线上的点也在集合C中,则C为凸集。
凸函数:对区间 [ a , b ] [a,b] [a,b]上定义的函数f,对任意两点 x 1 , x 2 x_1,x_2 x1,x2都有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})\le\frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2)
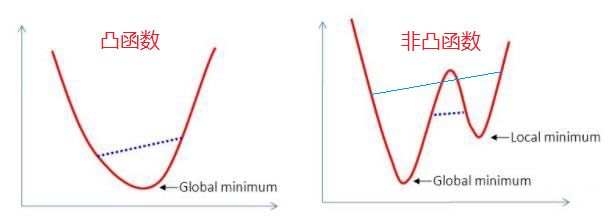
如 y = x 2 y=x^2 y=x2这种U型函数即为凸函数。
凸函数的局部极小值就是全局最小值,而非凸函数没有很好的解决最小值的方法,所以我们定义损失函数时尽量将其定义为凸优化问题或转换为等价凸优化问题,从而有助于求解。
θ j : = θ j − α ∂ ∂ θ j J ( θ ) ∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = 2 ⋅ 1 2 ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = ( h θ ( x ) − y ) x j \begin{aligned} \theta_{j}:=\theta_{j} &-\alpha \frac{\partial}{\partial \theta_{j}} J(\theta) \\ \frac{\partial}{\partial \theta_{j}} J(\theta) &=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2} \\ &=2 \cdot \frac{1}{2}\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right) \\ &=\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{n} \theta_{i} x_{i}-y\right) \\ &=\left(h_{\theta}(x)-y\right) x_{j} \end{aligned} θj:=θj∂θj∂J(θ)−α∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2=2⋅21(hθ(x)−y)⋅∂θj∂(hθ(x)−y)=(hθ(x)−y)⋅∂θj∂(i=0∑nθixi−y)=(hθ(x)−y)xj
损失函数
我们把要最小化或最大化的函数称为目标函数或准则。 当我们对其进行最小化时,我们也把它称为代价函数、损失函数或误差函数。
方向导数
导数的基础知识就不说了,理工科学生必会的,这里从方向导数开始讲。
我们知道函数 f ( x , y ) f(x,y) f(x,y)在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right ) (x0,y0)处的两个偏导数,分别是函数 f f f在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right ) (x0,y0)处沿与 x x x 轴和 y y y 轴平行的方向的变化率。
但是在许多实际问题中,还需要研究函数沿各个不同方向的变化率。例如,在大气气象中,就需要研究温度、气压沿不同方向的变化率。这就是所谓的方向导数。
方向导数本质是研究函数在某点处沿某特定方向的变化率问题。
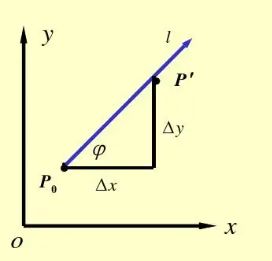
比如 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right ) (x0,y0)沿方向 l l l 的变化率。假设方向如图所示, l l l 为平面上一条射线, p ′ p^{'} p′ 为方向 l l l上的另一点。
由图可知, p \mathrm{p} p与 p ′ \mathrm{p}^{\prime} p′之间的距离 ∣ p p ′ ∣ = ρ = Δ x 2 + Δ y 2 \left|\mathrm{pp}^{\prime}\right|=\rho=\sqrt{\Delta \mathrm{x}^{2}+\Delta \mathrm{y}^{2}} ∣pp′∣=ρ=Δx2+Δy2
函数的增量 Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta \mathrm{z}=\mathrm{f}\left(\mathrm{x}_{0}+\Delta \mathrm{x}, \mathrm{y}_{0}+\Delta \mathrm{y}\right)-\mathrm{f}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) Δz=f(x0+Δx,y0+Δy)−f(x0,y0)
考虑函数的增量与这两点间距离的比值,当 p ′ p^{\prime} p′ 沿着方向 l l l趋于 p p p时,如果这个比的极限存在,则称这个极限为函数 f ( x , y ) f(x, y) f(x,y)在点 p p p沿方向 l l l的方向导数,记作 ∂ f ∂ l \frac{\partial f}{\partial l} ∂l∂f,即
∂ f ∂ l = lim ρ → 0 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) ρ \frac{\partial \mathrm{f}}{\partial \mathrm{l}}=\lim _{\rho \rightarrow 0} \frac{\mathrm{f}\left(\mathrm{x}_{0}+\Delta \mathrm{x}, \mathrm{y}_{0}+\Delta \mathrm{y}\right)-\mathrm{f}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right)}{\rho} ∂l∂f=ρ→0limρf(x0+Δx,y0+Δy)−f(x0,y0)
从定义可知,当函数 f ( x , y ) \mathrm{f}(\mathrm{x}, \mathrm{y}) f(x,y)在点 p ( x 0 , y 0 ) \mathrm{p}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) p(x0,y0)的偏导数 f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) \mathrm{f}_{\mathrm{x}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right), \mathrm{f}_{\mathrm{y}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) fx(x0,y0),fy(x0,y0)存在时,函数 f ( x , y ) \mathrm{f}(\mathrm{x}, \mathrm{y}) f(x,y) 在 p \mathrm{p} p点沿着 x \mathrm{x} x轴正向单位向量 e 1 = { 1 , 0 } \mathrm{e}_{1}=\{1,0\} e1={1,0} , y \mathrm{y} y轴正向单位向量 e 2 = { 0 , 1 } \mathrm{e}_{2}=\{0,1\} e2={0,1} 的方向导数存在,且其值依次为 f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) \mathrm{f}_{\mathrm{x}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) , \mathrm{f}_{\mathrm{y}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) fx(x0,y0),fy(x0,y0);
函数 f ( x , y ) \mathrm{f}(\mathrm{x}, \mathrm{y}) f(x,y) 在 p \mathrm{p} p点沿着 x \mathrm{x} x轴负向单位向量 e 1 ′ = { − 1 , 0 } \mathrm{e}_{1}^{\prime}=\{-1,0\} e1′={−1,0} , y \mathrm{y} y轴负向单位向量 e 2 ′ = { 0 , − 1 } \mathrm{e}_{2}^{\prime}=\{0,-1\} e2′={0,−1} 的方向导数存在,且其值依次为 − f x ( x 0 , y 0 ) , − f y ( x 0 , y 0 ) -\mathrm{f}_{\mathrm{x}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) ,-\mathrm{f}_{\mathrm{y}}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right) −fx(x0,y0),−fy(x0,y0)
方向导数 ∂ f ∂ 1 \frac{\partial \mathrm{f}}{\partial 1} ∂1∂f的存在及计算如下定理。
如果函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) \left ( x_{0},y_{0} \right) (x0,y0) 是可微分的,那么函数在该点沿任意方向 l l l 的方向导数都存在,且有
∂ f ∂ l = ∂ f ∂ x c o s φ + ∂ f ∂ y s i n φ \frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}cos\varphi +\frac{\partial f}{\partial y}sin\varphi ∂l∂f=∂x∂fcosφ+∂y∂fsinφ
其中 φ \varphi φ 为 x x x 轴到 l l l 方向的转角。
方向导数的几何意义
方向导数的几何意义如图所示,函数 z = f ( x , y ) z=f(x, y) z=f(x,y) 的变化方向为 l l l,方向导数 ∂ f ∂ l ∣ p \left.\frac{\partial f}{\partial l}\right|_{p} ∂l∂f∣ ∣p 是函数 z = f ( x , y ) z=f(x, y) z=f(x,y) 在点 p p p 处沿方向 l l l的变化率,从方向 l l l作垂直于 x O y \mathrm{xOy} xOy 平面的一个平面,与曲面相交成一条曲线 M Q , ∂ f ∂ l ∣ p \left.\mathrm{M} Q , \frac{\partial \mathrm{f}}{\partial l}\right|_{\mathrm{p}} MQ,∂l∂f∣ ∣p即为曲线 M Q \mathrm{MQ} MQ 在 M \mathrm{M} M点的切线 M N \mathrm{MN} MN 的斜率。
点 p \mathrm{p} p 在某一方向的变化率,就是过曲面 M \mathrm{M} M 点的某一条曲线的切线的斜率。
根据曲面的切平面与法线的相关概念可知,曲面上通过点 M \mathrm{M} M 且在点 M \mathrm{M} M 处具有切线的曲线,它们在点 M \mathrm{M} M 处的切线都在同一个平面上,这个平面称为切平面。
因此方向导数 ∂ f ∂ 1 ∣ p \left.\frac{\partial \mathrm{f}}{\partial 1}\right|_{\mathrm{p}} ∂1∂f∣ ∣p 为过 M \mathrm{M} M 点的切平面上的某条直线的斜率,那么哪一个方向的变化率最大呢?
大多数机器学习或者深度学习算法都涉及某种形式的优化。 优化指的是改变 x x x 以最小化或最大化某个函数$f(x) 的任务。我们通常以最小化 的任务。 我们通常以最小化 的任务。我们通常以最小化f(x) 指代大多数最优化问题。最大化可经由最小化算法最小化 指代大多数最优化问题。 最大化可经由最小化算法最小化 指代大多数最优化问题。最大化可经由最小化算法最小化-f(x)$ 来实现。
梯度
梯度在一元函数中称为导数,某点的导数就是函数在该点的斜率,即函数的变化率。我们求一元函数极小值时要先求一阶导数为0的点,然后带入就是极小值了(注意是极小值不是最小值)。
梯度定义:设 n \mathrm{n} n 元函数 f ( x ) f(\boldsymbol{x}) f(x) 对自变量 x = ( x 1 , x 2 , … , x n ) T \boldsymbol{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)^{T} x=(x1,x2,…,xn)T 的各分量 x i x_{i} xi 的偏导数 ∂ f ( x ) ∂ x i ( i = 1 , 2 , … , n ) \frac{\partial f(\boldsymbol{x})}{\partial x_{i}}(i=1,2, \ldots, n) ∂xi∂f(x)(i=1,2,…,n)都存在,则称函数 f ( x ) f(\boldsymbol{x}) f(x) 在$ \boldsymbol{x}$ 处一阶可导, 并称向量
∇ f ( x ) = ( ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ) \nabla f(\boldsymbol{x})=\left(\begin{array}{c} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right) ∇f(x)=⎝ ⎛∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎠ ⎞
为函数 f ( x ) f(\boldsymbol{x}) f(x) 在 x \boldsymbol{x} x 处的一阶导数或梯度, 记为 ∇ f ( x ) \nabla f(\boldsymbol{x}) ∇f(x)(列向量)
梯度的本意是一个向量(一个函数的全部偏导数构成的向量),表示某一函数在该点处方向导数沿着该方向取得的最大值,即函数沿梯度的方向变化最快,变化率最大(为该梯度的模)。
在曲面上方向导数的最大值的方向就代表了梯度的方向,因此我们在做梯度下降的时候,应该是沿着梯度的反方向进行权重的更新,可以有效的找到全局的最优解。
梯度下降
凸优化问题同一表述为求函数极小值问题,遇到求极大值时,在目标函数前面加个负号,从而转为极小值问题求解。
目标函数的自变量x往往受到各种约束,满足约束条件的自变量x的集合称为自变量的可行域。
梯度下降是一种逐步迭代,逐步缩减损失函数值,从而使损失函数最小的方法。
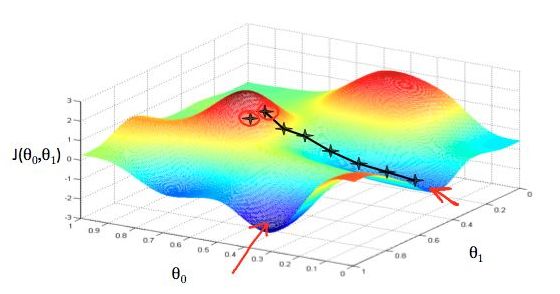
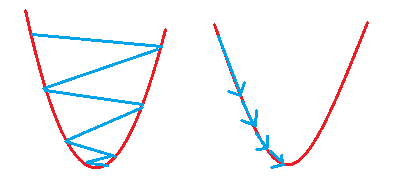
在直观上,我们可以这样理解,看下图,一开始的时候我们随机站在一个点(初始化参数),把他看成一座山,每一步,我们都以下降最多的路线方向(负梯度方向)来下山,那么,在这个过程中我们到达山底(最优点)是最快的,而上面的a,它决定了我们“向下山走”时每一步的大小,过小的话收敛太慢,过大的话可能错过最小值)。这是一种很自然的算法,每一步总是寻找使J下降“陡”的方向(就像找最快下山的路一样)。
然后就是确定步长,下山的起始点和每一步的反向知到了,那么一步该走多长呢?
如果步长太大,虽然能快速逼近山谷,但可能跨过了山谷,造成来回震荡;如果太小则可能延长了到达山谷底部的时间。
每次走多大的距离,就是所谓的学习率,如何设置学习率需要反复调试很吃工程师的经验。
梯度下降的迭代公式如下:
θ 1 = θ 0 − α ∇ J ( θ ) \theta^1=\theta^0-\alpha \nabla J(\theta) θ1=θ0−α∇J(θ)
其含义是:任意给定一组初始参数值 θ 0 \theta ^0 θ0,沿着损失函数, J ( θ ) J(\theta) J(θ) 的梯度下降方向前进一段距离 α \alpha α,就可以得到一组新的参数值 θ 1 \theta^1 θ1,这里的 θ 0 , θ 1 \theta^0,\,\theta^1 θ0,θ1,对应到中就是指模型参数(如w和b)。
具体求解
最常用的一个损失函数:均方误差
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ) − y ) 2 J(\theta)=\frac{1}{2}\sum_{i=1}^{m}({h_\theta(x)-y})^2 J(θ)=21i=1∑m(hθ(x)−y)2
其中 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 . . . . + θ n x n h_θ(x)=θ_0+θ_1x_1+θ_{2}x_2....+θ_{n}x_n hθ(x)=θ0+θ1x1+θ2x2....+θnxn ,对该函数进行优化。用最小二乘法我们在一元线性回归中已经推过了,这里用梯度下降法来解。
先求 θ j \theta_j θj的偏导数:
∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = 2 ⋅ 1 2 ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = ( h θ ( x ) − y ) x j \begin{aligned} \frac{\partial}{\partial \theta_{j}} J(\theta) &=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2} \\ &=2 \cdot \frac{1}{2}\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right) \\ &=\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{n} \theta_{i} x_{i}-y\right) \\ &=\left(h_{\theta}(x)-y\right) x_{j} \end{aligned} ∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2=2⋅21(hθ(x)−y)⋅∂θj∂(hθ(x)−y)=(hθ(x)−y)⋅∂θj∂(i=0∑nθixi−y)=(hθ(x)−y)xj
这样就确定了下降的方向:
θ j + 1 = θ j + α ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_{j+1}=\theta_{j}+\alpha \sum_{i=1}^{m}\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)}\\ θj+1=θj+αi=1∑m(y(i)−hθ(x(i)))xj(i)
设 J ( θ ) = θ 1 2 + θ 2 2 J(\theta)=\theta_1^2+\theta_2^2 J(θ)=θ12+θ22,显然这个函数在 ( 0 , 0 ) (0,0) (0,0)处取得最小值。
假设起始值 θ 0 = ( 4 , − 2 ) \theta^0=(4,-2) θ0=(4,−2),学习率 α = 0.1 \alpha=0.1 α=0.1, ∇ J ( θ ) = ( 2 θ 1 , 2 θ 2 ) \nabla J(\theta)=(2\theta_1,2\theta_2) ∇J(θ)=(2θ1,2θ2)。历次迭代结果看多元函数梯度下降代码
批量梯度下降
在每次更新时用所有样本,要留意,在梯度下降中,对于 $θ_i 的更新,所有的样本都有贡献,也就是参与调整 的更新,所有的样本都有贡献,也就是参与调整 的更新,所有的样本都有贡献,也就是参与调整 θ$.其计算得到的是一个标准梯度,**对于最优化问题,凸问题,**也肯定可以达到一个全局最优。因而理论上来说一次更新的幅度是比较大的。
如果样本不多的情况下,当然是这样收敛的速度会更快啦。但是很多时候,样本很多,更新一次要很久,这样的方法就不合适啦。下图是其更新公式
θ j : = θ j + α ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_{j}:=\theta_{j}+\alpha \sum_{i=1}^{m}\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)} θj:=θj+αi=1∑m(y(i)−hθ(x(i)))xj(i)
随机梯度下降(SGD)
SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次,在样本量及其大的情况下,可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。(重点:每次迭代使用一组样本。)
为什么叫随机梯度下降算法呢?这里的随机是指每次迭代过程中,样本都要被随机打乱,这个也很容易理解,打乱是有效减小样本之间造成的参数更新抵消问题。
对于权值的更新不再通过遍历全部的数据集,而是选择其中的一个样本即可。一般来说其步长的选择比梯度下降法的步长要小一点,因为梯度下降法使用的 是准确梯度,所以它可以朝着全局最优解(当问题为凸问题时)较大幅度的迭代下去,但是随机梯度法不行,因为它使用的是 近似梯度,或者对于全局来说有时候它走的也许根本不是梯度下降的方向,故而它走的比较缓,同样这样带来的好处就是相比于梯度下降法,它不是那么容易陷入到局部最优解中去。
代码实现
一元函数梯度下降
import numpy as np
import matplotlib.pyplot as plt
# 自定义一个函数
plot_x = np.linspace(-6, 8., 200)
plot_y = (plot_x-1)**2 - 1.
# 当两次迭代的距离 小于epsilon时停止迭代
epsilon = 1e-5
# 学习率
eta = 0.1
# 原函数,最小值为 -1
def J(theta):
return (theta-1)**2 - 1.
# 梯度
def dJ(theta):
return 2*(theta-1)
# 初始化theta为3
theta = -5
# 记录每次的梯度值
theta_history = [theta]
# 迭代
while True:
# 求梯度值
gradient = dJ(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if(abs(J(theta) - J(last_theta)) < epsilon):
break
plt.figure(figsize=(10,8))
plt.plot(plot_x, J(plot_x),)
plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker='o')
plt.show()
print("迭代次数:{}".format(len(theta_history)))
print(theta)
print(J(theta))
多元梯度下降
import mpl_toolkits.mplot3d
x,y = np.mgrid[-2:2:20j,-2:2:20j]
z=(x**2+y**2)
ax = plt.subplot(111,projection='3d')
ax.plot_surface(x,y,z,rstride = 9, cstride = 1, cmap = plt.cm.Blues_r)
plt.show()
# 多元函数的梯度
def grad_2(p):
derivx = 2*p[0]
derivy = 2*p[1]
return np.array([derivx,derivy])
# 梯度下降函数
def grad_descent(grad,p_current,learn_rate,iter_max):
for i in range(iter_max):
print("第:{}次迭代, p值为{}".format(i,p_current))
grad_current =grad(p_current)
if np.linalg.norm(grad_current,ord=2)< 1e-5:
break
else:
p_current=p_current-grad_current*learn_rate
print("极小值为: ".format(p_current))
return p_current
grad_descent(grad_2,np.array([1,-1]),0.1, 100)
----
第:0次迭代, p值为[ 1 -1]
第:1次迭代, p值为[ 0.8 -0.8]
第:2次迭代, p值为[ 0.64 -0.64]
第:3次迭代, p值为[ 0.512 -0.512]
第:4次迭代, p值为[ 0.4096 -0.4096]
第:5次迭代, p值为[ 0.32768 -0.32768]
第:6次迭代, p值为[ 0.262144 -0.262144]
第:7次迭代, p值为[ 0.2097152 -0.2097152]
第:8次迭代, p值为[ 0.16777216 -0.16777216]
第:9次迭代, p值为[ 0.13421773 -0.13421773]
第:10次迭代, p值为[ 0.10737418 -0.10737418]
第:11次迭代, p值为[ 0.08589935 -0.08589935]
第:12次迭代, p值为[ 0.06871948 -0.06871948]
第:13次迭代, p值为[ 0.05497558 -0.05497558]
第:14次迭代, p值为[ 0.04398047 -0.04398047]
第:15次迭代, p值为[ 0.03518437 -0.03518437]
第:16次迭代, p值为[ 0.0281475 -0.0281475]
第:17次迭代, p值为[ 0.022518 -0.022518]
第:18次迭代, p值为[ 0.0180144 -0.0180144]
第:19次迭代, p值为[ 0.01441152 -0.01441152]
第:20次迭代, p值为[ 0.01152922 -0.01152922]
第:21次迭代, p值为[ 0.00922337 -0.00922337]
第:22次迭代, p值为[ 0.0073787 -0.0073787]
第:23次迭代, p值为[ 0.00590296 -0.00590296]
第:24次迭代, p值为[ 0.00472237 -0.00472237]
第:25次迭代, p值为[ 0.00377789 -0.00377789]
第:26次迭代, p值为[ 0.00302231 -0.00302231]
第:27次迭代, p值为[ 0.00241785 -0.00241785]
第:28次迭代, p值为[ 0.00193428 -0.00193428]
第:29次迭代, p值为[ 0.00154743 -0.00154743]
第:30次迭代, p值为[ 0.00123794 -0.00123794]
第:31次迭代, p值为[ 0.00099035 -0.00099035]
第:32次迭代, p值为[ 0.00079228 -0.00079228]
第:33次迭代, p值为[ 0.00063383 -0.00063383]
第:34次迭代, p值为[ 0.00050706 -0.00050706]
第:35次迭代, p值为[ 0.00040565 -0.00040565]
第:36次迭代, p值为[ 0.00032452 -0.00032452]
第:37次迭代, p值为[ 0.00025961 -0.00025961]
第:38次迭代, p值为[ 0.00020769 -0.00020769]
第:39次迭代, p值为[ 0.00016615 -0.00016615]
第:40次迭代, p值为[ 0.00013292 -0.00013292]
第:41次迭代, p值为[ 0.00010634 -0.00010634]
第:42次迭代, p值为[ 8.50705917e-05 -8.50705917e-05]
第:43次迭代, p值为[ 6.80564734e-05 -6.80564734e-05]
第:44次迭代, p值为[ 5.44451787e-05 -5.44451787e-05]
第:45次迭代, p值为[ 4.3556143e-05 -4.3556143e-05]
第:46次迭代, p值为[ 3.48449144e-05 -3.48449144e-05]
第:47次迭代, p值为[ 2.78759315e-05 -2.78759315e-05]
第:48次迭代, p值为[ 2.23007452e-05 -2.23007452e-05]
第:49次迭代, p值为[ 1.78405962e-05 -1.78405962e-05]
第:50次迭代, p值为[ 1.42724769e-05 -1.42724769e-05]
第:51次迭代, p值为[ 1.14179815e-05 -1.14179815e-05]
第:52次迭代, p值为[ 9.13438523e-06 -9.13438523e-06]
第:53次迭代, p值为[ 7.30750819e-06 -7.30750819e-06]
第:54次迭代, p值为[ 5.84600655e-06 -5.84600655e-06]
第:55次迭代, p值为[ 4.67680524e-06 -4.67680524e-06]
第:56次迭代, p值为[ 3.74144419e-06 -3.74144419e-06]
第:57次迭代, p值为[ 2.99315535e-06 -2.99315535e-06]
极小值为:[ 2.99315535e-06 -2.99315535e-06]