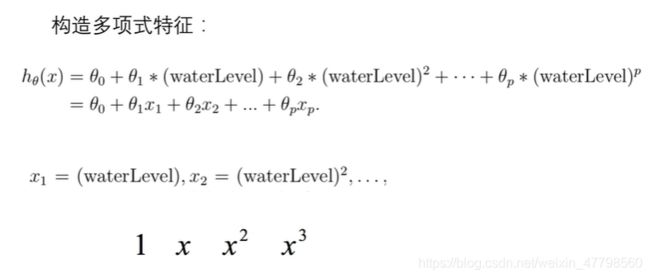吴恩达机器学习ex5:偏差和方差
吴恩达机器学习作业五:偏差和方差
在本练习中,您将实现正则化线性回归,并使用它来研究具有不同偏差方差特性的模型。
#coding=utf-8
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from scipy.io import loadmat
from sklearn.metrics import classification_report
1 Regularized Linear Regression
在练习的前半部分,您将实现正则化线性回归,以使用水库水位的变化来预测从大坝流出的水量。在下半部分中,您将经历一些调试学习算法的诊断,并检查偏差与方差的影响。
1.1 Visualizing the dataset
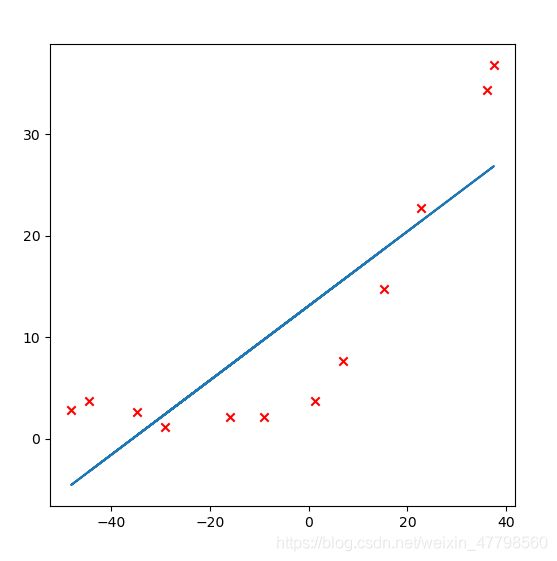
我们将首先可视化数据集,其中包含水位变化的历史记录x和流出大坝的水量y。

ex5.m的下一步将绘制训练数据。在下面的部分中,您将实现线性回归,并使用它来拟合数据的直线并绘制学习曲线。接下来,您将实现多项式回归以找到更适合数据的方法。
# 读取数据
def load_data(path):
data = loadmat(path)
X = data['X']
y = data['y']
Xval = data['Xval']
yval = data['yval']
Xtest = data['Xtest']
ytest = data['ytest']
return X,y,Xval,yval,Xtest,ytest
path = 'D:\编程\ex5data1.mat'
X,y,Xval,yval,Xtest,ytest = load_data(path)
print(X.shape,y.shape,Xval.shape,yval.shape,Xtest.shape,ytest.shape)
# 可视化数据集
plt.figure(figsize=(5,5),dpi=50)
plt.scatter(X,y,marker='x',color = 'red')
plt.xlabel('Change in water levle(x)')
plt.ylabel('water flowing out of the dam(y)')
plt.show()
X = np.insert(X,0,values=1,axis=1)
Xval = np.insert(Xval,0,values=1,axis=1)
Xtest = np.insert(Xtest,0,values=1,axis=1)
print(X.shape,y.shape,Xval.shape,yval.shape,Xtest.shape,ytest.shape)
1.2 Regularized linear regression cost function

其中λ是控制正则化程度的正则化参数(因此,有助于防止过度拟合)。正则化项对总成本J有惩罚,随着模型参数θJ的增大,惩罚也随之增大。注意,不应该正则化θ0项。您的任务是编写一个函数来计算正则化线性回归代价函数。如果可能的话,尽量将代码矢量化,避免编写循环。完成后,应该期望看到303.993的输出。
# 正则化线性回归损失函数
# 记得:不惩罚theta0!!!
def regular_costfunction(theta,X,y,lam):
theta = theta.reshape(1, X.shape[1])
one = np.sum(np.power(X @ theta.T - y,2)) / (2*len(X))
two = np.sum(np.power(theta[1:],2)) * lam /(2*len(X))
return one+two
theta = np.ones(X.shape[1]).reshape(X.shape[1],1)
print(regular_costfunction(theta,X,y,1))
# 303.9931922202643
1.3 Regularized linear regression gradient
# 线性回归梯度下降
def gradient(theta,X,y):
return (X @ theta.T - y).T @ X / len(X)
# 正则化线性函数梯度下降
def regular_gradient(theta,X,y,lam):
theta = theta.reshape(1,X.shape[1])
theta_reg = theta.copy()
first = gradient(theta, X, y)
theta_reg[0,0] = 0
reg = theta_reg * lam / len(X)
return first+ reg
1.4 Fitting linear regression
# 拟合线性回归
def fit_reg(X,y,lam):
theta = np.zeros(X.shape[1])
# res = opt.fmin_tnc(func=regular_costfunction, x0=theta, fprime=regular_gradient, args=(X, y,lam ))
res = opt.minimize(fun=regular_costfunction,x0=theta,args=(X,y,lam),method='TNC',jac=regular_gradient)
final_theta = res.x
return final_theta
lam = 0 # 因为我们现在训练的是2维的,所以正则化不会对这种低维的有很大的帮助。
print(fit_reg(X,y,lam))
# 可视化
t = X @ final_theta.T
plt.figure(figsize=(6,6),dpi = 50)
plt.plot(X[:,1],t)
plt.scatter(X[:,1:],y,marker='x',c='r')
plt.show()
2 Bias-variance
机器学习中的一个重要概念是偏差-方差权衡。高偏差模型对数据的拟合不够复杂,容易出现欠拟合,而高方差模型对训练数据的拟合过度。
在这部分练习中,您将在学习曲线上绘制训练和测试错误,以诊断偏差-方差问题。
2.1 Learning curves
# 偏差和方差
# 1.学习曲线
def learning_curves(X,y,Xval,yval,lam):
train_cost = []
cv_cost = []
XX = range(1, X.shape[0] + 1)
for i in range(1,X.shape[0]+1):
train_theta = fit_reg(X[:i],y[:i],lam)
train_costi = regular_costfunction(train_theta,X[:i],y[:i],lam)
train_cost.append(train_costi)
cv_costi = regular_costfunction(train_theta,Xval,yval,lam)
cv_cost.append(cv_costi)
plt.figure(figsize=(6,6),dpi=80)
plt.plot(XX,train_cost,c = 'g',label = 'training cost')
plt.plot(XX,cv_cost,c = 'b',label = 'cv cost')
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.title('Learning curve for linear regression')
plt.legend()
plt.show()
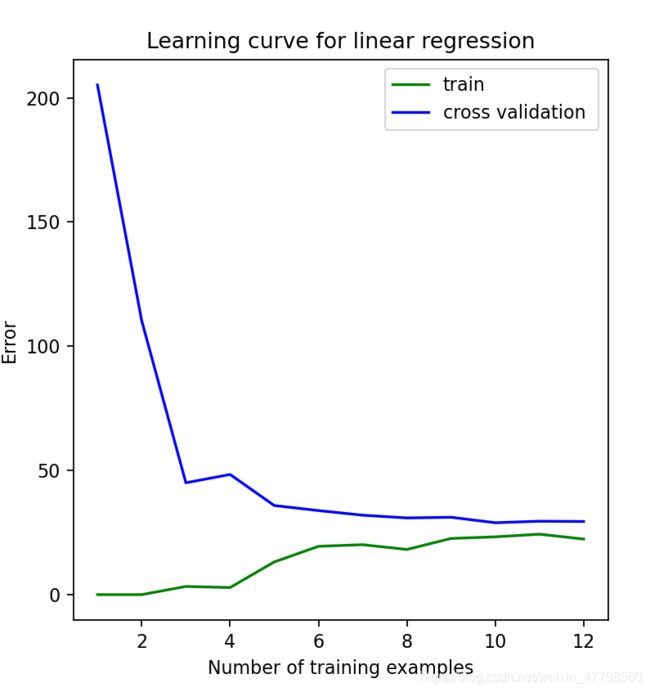
从图中可以看出,随着训练样本集的不断增加,训练集的损失函数很高且训练集的损失函数近似等于交叉验证集的损失函数。由此可以看出这是一个高偏差问题(Bias),也就是欠拟合(underfit)。
3 Polynomial regression
3.1 Learning Polynomial Regression
# 多项式回归
# 构造特征多项式
def poly_feature(X,power):
Xpoly = X.copy()
for j in range(2,power+1):
# 这样能一直保持在X的最后一列插入
Xpoly= np.insert(Xpoly,Xpoly.shape[1],values=np.power(Xpoly[:,1],j),axis=1)
return Xpoly
# 特征归一化处理
def mean_std(x):
mean = np.mean(x,axis = 0)
std = np.std(x,axis = 0,ddof = 1)
return mean,std
def feature_normal(x,mean,std):
x[:,1:] = (x[:,1:] - mean[1:]) / std[1:]
return x
# 训练集
Xtrain_poly = poly_feature(X,6) # 获取特征多项式
train_mean,train_std = mean_std(Xtrain_poly)
train_normal = feature_normal(Xtrain_poly,train_mean,train_std) # 归一化处理
# 交叉验证集
Xcv_poly = poly_feature(Xval,6)
cv_normal = feature_normal(Xcv_poly,train_mean,train_std)
# 测试集
Xtest_poly = poly_feature(Xtest,6)
test_normal = feature_normal(Xtest_poly,train_mean,train_std)
theta = fit_reg(train_normal, y,0)
# 绘制拟合曲线
def plot_fit_curve():
x = np.linspace(-80,60,100)
print("x:{}".format(x.shape))
x1 = x.reshape(100,1)
x1 = np.insert(x1,0,values=1,axis=1)
x1 = poly_feature(x1,6)
x1 = feature_normal(x1,train_mean,train_std)
y1 = x1 @ theta
plt.figure(figsize=(6,6),dpi=50)
plt.scatter(X[:,1],y,marker='x',color = 'red')
# 坐标轴范围
plt.xlim(-100,80)
plt.ylim(-80,60)
# 坐标轴刻度
xtick = np.arange(-100,80,20)
ytick = np.arange(-80,60,20)
plt.xticks(xtick)
plt.yticks(ytick)
plt.xlabel("Change in water level(x)")
plt.ylabel("Water flowing out of the dam(y)")
plt.plot(x,y1,'b--')
plt.show()
print(plot_fit_curve())
print(learning_curves(train_normal,y,cv_normal,yval,0))
此图为lam=1时的拟合曲线。


我们从图中可以看出,当lam = 1时,训练误差太小了。明显产生了过拟合。

3.2 Optional (ungraded) exercise: Adjusting the regularization parameter
为了更好的了解正则化参数如何影响正则化多项式回归的偏差方差。现在应该修改lambda参数,并尝试λ=1100。对于这些值中的每一个,脚本都应该生成一个多项式来拟合数据和一条学习曲线。
当lam = 1如下图:


这显示了λ =1正则多项式回归模型不存在高偏或高方差问题。实际上,它在偏差和方差之间取得了很好的平衡。
当lam = 100时,如下图:
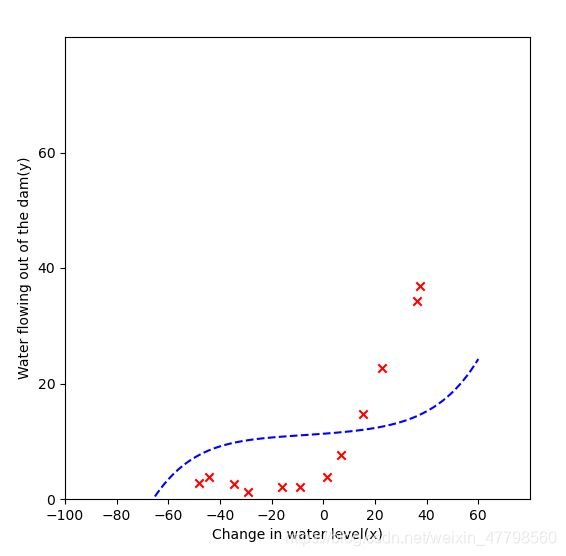

对于λ=100,可以看到看到多项式拟合没有很好地遵循数据。在这种情况下,有太多的正则化和模型无法拟合的训练数据。
3.3 Selecting λ using a cross validation set
在前面的练习中,您注意到λ的值会显著影响训练集和交叉验证集上正则化多项式回归的结果。特别地,没有正则化的模型(λ=0)很好地拟合了训练集,但不能推广。相反地,正则化过多(λ=100)的模型不能很好地拟合训练集和测试集。选择好λ(例如λ=1)可以很好地拟合数据。
在本节中,您将实现自动选择λ参数的方法。具体来说,您将使用交叉验证集来评估每个λ值有多好。在使用交叉验证集选择最佳λ值之后,我们可以在测试集上评估模型,以估计模型在实际看不到的数据上的性能。
具体来说,您应该使用trainLinearReg函数使用不同的λ值来训练模型,并计算训练误差和交叉验证误差。应在以下范围内尝试λ:{0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10}。
lam_list = [0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
y_error_list = []
yval_error_list = []
for l in lam_list:
lam = l
theta = fit_reg(train_normal, y, lam)
# 注意:当计算训练集、交叉验证集和测试集误差时,不计算正则项
y_error = regular_costfunction(theta,train_normal,y,lam=0)
y_error_list.append(y_error)
yval_error = regular_costfunction(theta,cv_normal,yval,lam=0)
yval_error_list.append(yval_error)
plt.figure(figsize=(6,6),dpi = 50)
plt.xlabel('lambda')
plt.ylabel('Error')
plt.plot(lam_list,y_error_list,c = 'g',label = 'train')
plt.plot(lam_list,yval_error_list,c = 'b',label = 'cross validation')
plt.legend()
plt.show()
# 可以看到时交叉验证代价最小的是 lambda = 3
print("交叉验证代价最小的是lambda = {}".format(lam_list[np.argmin(yval_error_list)])) # 3.0
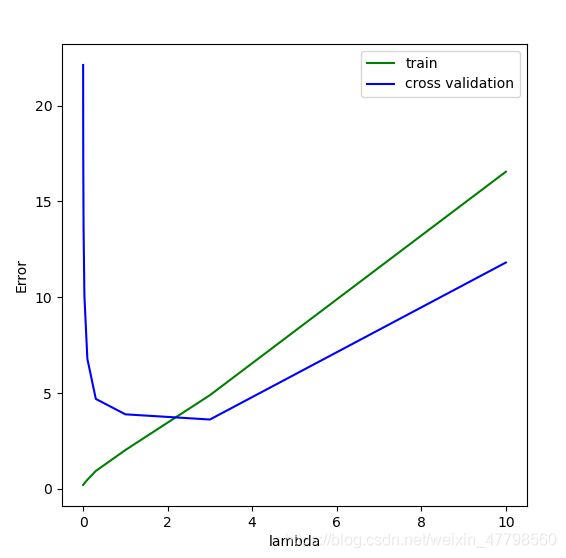
在这个图中,我们可以看到λ的最佳值在3左右。由于数据集的训练和验证分裂具有随机性,交叉验证误差有时会低于训练误差。
3.4 Optional (ungraded) exercise: Computing test set error
在本练习的上一部分中,实现了用于计算正则化参数的各种值的交叉验证错误的代码λ. 然而,为了更好地了解模型在现实世界中,评估“最终的” 在训练的任何部分都没有使用的测试集上的模型(也就是说,它既没有用于选择λ 参数,也不学习模型参数θ). 对于这个可选(未分级)练习,您应该使用你已经找到的λ。在我们的交叉验证中,我们得到的测试误差为3.8599,λ = 3.
theta = fit_reg(train_normal, y, 3)
test_cost = regular_costfunction(theta,test_normal,ytest,3)
print("test_cost(lambda = 3) = {}".format(test_cost))

由于特征映射部分power=6来实现的,所以得不到3.8599。但是调整power=8时(同作业里一样),就可以得到上述数据。
3.5 Optional (ungraded) exercise: Plotting learning curves with randomly selected examples
在实践中,特别是对于小的训练集,当您绘制学习曲线以调试算法时,在多个随机选择的示例集上求平均值通常是有帮助的,以确定训练错误和交叉验证错误。具体来说,要确定i个例子的训练误差和交叉验证误差,首先要从训练集中随机选择i个例子,从交叉验证集中随机选择i个例子。然后,您将使用随机选择的训练集学习参数θ,并在随机选择的训练集和交叉验证集上评估参数θ。然后应重复上述步骤多次(例如50次),并且应使用平均误差来确定i示例的训练误差和交叉验证误差。对于这个可选(未分级)练习,您应该实现上面的策略来计算学习曲线。