R数据分析:交叉滞后模型非专业解释
今天继续写交叉滞后模型,本文大部分内容参考自文献:Kearney, Michael. (2017). Cross-Lagged Panel Analysis.
所以不论自己写的怎么样都建议大家去瞅瞅原文章哦,原文很短的。
什么是交叉滞后
交叉滞后模型是一种研究变量相互关系的分析方法,它的名字有交叉滞后面板模型Cross-lagged panel models (CLPM),交叉滞后路径模型,交叉滞后回归模型,指的都是同一个东西。
为啥叫”交叉“?
因为它同时既研究A对B的关系,又研究B对A的关系。
为啥叫”滞后“?
因为它研究不同时间点变量间的关系。
把下面的话记住:
交叉滞后在本质上要干的事就是比较时点1X和时点2Y的关系与时点1Y和时点2X关系的差异,从而更好地理解XY到底是如何相互影响的。
In essence, cross-lagged panel analysis compares the relationship between variable X at Time 1 and variable Y at Time 2 with the relationship between variable Y at Time 1 and X at Time 2. It is widely used to examine the stability and relationships between variables over time to better understand how variables influence each other over time
变量关系的方向性
传统的我们熟知的探究变量关系的方法都或多或少有局限,比如做相关时我们想得到X和Y的因果关系只能靠理论基础,因为相关本身不说明问题。横断面数据也不能判断因果。
随机对照试验可以,但是很多时候现实条件不允许你去做试验。
这种情况下,研究者开始求助纵向数据和交叉滞后模型。
交叉滞后相关
Cross-lagged correlations (CLC)交叉滞后相关认为,变量间的关系是相互的,如果两个系数(x1影响y2的系数和y1影响x2的系数)是一样的话,就认为确实两个变量影响是相互的,但如果一个系数显著的比另外一个大,则认为关系是单向的。
好像有点道理哈,但是仔细想想:
上面的流程没有考虑变量间关系的暂时关系(contemporaneous relationships),就是说上面的方法忽略了x1对y1的影响和y1与x1的影响等等,还有上面的流程没有考虑xy本身随时间的变化,所以是不可取的。
交叉滞后面板模型
这个东西比较差滞后相关多考虑了一些事,它不止估计交叉滞后效应,同时也会把时点相关和自回归效应考虑进去。
自回归是啥?
Autoregressive effects describe the amount of stability in constructs over time
就是你要研究的变量随时间的改变,自回归系数越小说明变量随时间变异越大,自回归系数越大说明变量随时间变异越小。
仔细体会红字,我并没有写错。
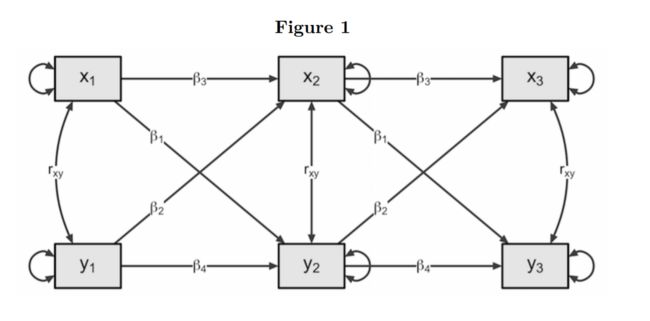
那么,一个最基本的交叉滞后面板模型就包括XY两个变量,每个变量就测两次。于是我们有x1,x2和y1,y2共4个变量,这个时候,x1y1,x2y2有相关,x1x2,y1y2有自回归,还有交叉滞后回归系数x1y2,y1x2。加上两个内生残差和两个外生残差,共10个参数模型就可以恰好识别。
怎么做呢?就是把这个模型拟合好,然后比较交叉滞后路径系数就行。
同样的流程可以扩展到多个时间点的数据,比如我们有3个时间点:
示意图如上,本来上图应该有4个交叉滞后路径系数,但是我们给他固定为2个了,我们认为从时点1到时点2和从时点2到时点3xy的关系应该是一样的。相应的自回归系数也进行了固定,我们认为只有x1能影响x2,而x1对x3并没有影响,同样的x1也不会影响y3,这个叫做滞后一个单位。
当然,上面的设定都是可以随着研究变的。
交叉滞后面板模型的假设
- 同步性假设Synchronicity
The first is the assumption of synchronicity, which assumes that measurements at each time point occurred at the exact same times.
意思是每一波数据都是在一个时刻收集的。
- 稳定性假设Stationarity
This assumption, referred to as stationarity, relates to the stability of a construct as well as the nature of the relationships between constructs over time
变量间跨时间的关系是稳定的。就是说x1y2的关系应该和x2y3的关系一样。
交叉滞后模型的解释
这部分还是给大家一个最简单的例子:
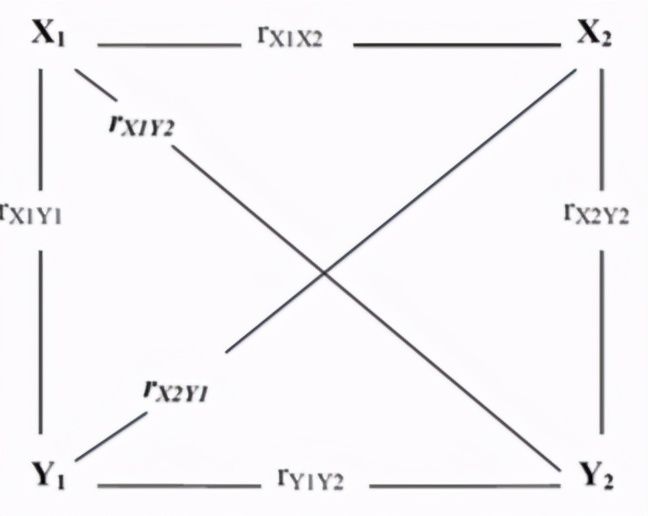
对于上面这个只有两个变量,而且只测了两次的数据的交叉滞后模型,我们有:
If rX1Y2 is ‘substantially different’ from zero, we can conclude that X causes Y.
If rX2Y1 is substantially different from zero, we can conclude that Y causes X.
If both are significantly different from zero, we conclude that X causes Y and Y causes X,
If both are equal we conclude that they do not cause each other but are both affected by a third variable.
看交叉滞后系数,如果交叉滞后系数rX1Y2显著不等于0,那么就是X影响Y,如果rX2Y1显著地不等于0,那么就是Y影响X,如果都显著就是相互影响。
小结
今天给大家写了交叉滞后面板模型的基本知识和解释,感谢大家耐心看完,自己的文章都写的很细,代码都在原文中,希望大家都可以自己做一做,请关注后私信回复“数据链接”获取所有数据和本人收集的学习资料。如果对您有用请先收藏,再点赞转发。
也欢迎大家的意见和建议,大家想了解什么统计方法都可以在文章下留言,说不定我看见了就会给你写教程哦。