论文笔记 Feature Selective Anchor-Free Module for Single-Shot Object Detection - CVPR 2019

2019 FSAF Feature Selective Anchor-Free Module for Single-Shot Object Detection

Chenchen Zhu, Yihui He CVPR, 2019 PDF

19年的这几篇论文非常相似，针对启发式 Anchor-Based 网络只能获取次优解的问题，提出了 Anchor Free 的网络，以下是19年的四篇 Anchor-Free 的模型：

Anchor-Free	Feature Selective Anchor-Free Module for Single-Shot Object Detection	CVPR, 2019
	FCOS: Fully Convolutional One-Stage Object Detection	ICCV, 2019
	FoveaBox: Beyond Anchor-based Object Detector	TIP, 2019
	Center and Scale Prediction: Anchor-free Approach for Pedestrian and Face Detection	CVPR, 2019

想想还是有点有趣，YOLO V2 使用 Faster R-CNN 中的 anchor 提升了模型的性能，但是基于 Anchor-Based 的模型，基于人工经验规则将不同尺寸的 Anchor-Boxes 分散到了不同的特征层，这样的结果显然就是 Sub-Optimal 的。

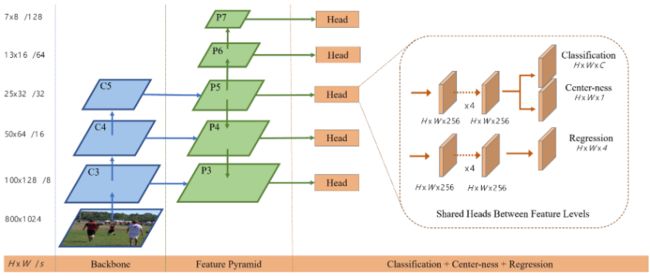
以下是这四个模型的 detection head，基本都是 2 个分支，一个预测类别，输出 $H\times W\times K$，另一个预测边框的相对坐标，输出大小为 $H\times W\times 4$。方法 2 除了这两个分支之外，还增加了一个 regression branch 来预测每个点到 ground truth 中心的远近程度。

Feature Selective Anchor-Free Module for Single-Shot Object Detection

FCOS: Fully Convolutional One-Stage Object Detection

FoveaBox: Beyond Anchor-based Object Detector

Center and Scale Prediction: Anchor-free Approach for Pedestrian and Face Detection

更多关于 Anchor-Based 和 Anchor-Free 可参照参考博文1.

摘要

FSAF 模块解决了传统的 Anchor-Based 的检测带来的两个限制：

• heuristic-guided feature selection
• overlap-based anchor sampling

FSAF 的基本概念是，将 online feature selection 应用在 multi-level anchor-free branches 的训练中。即特征金字塔的每一层都跟有一个 anchor-free branch，从而可以在任何一个特征层对 box 进行编码解码。在训练期间，我们动态地将每个 ground-true box 分配给最合适的特征层（这也就是 online feature selection 了）。在推理时，FSAF 模块可以通过并行输出预测与 anchor-based branch 联合工作。

1. Introduction

对象检测的一个具有挑战性的问题是尺度变化。为了实现尺度不变性，SOTA的检测器构建feature pyramids或multi-level feature towers。并且特征图的多个尺度级别正在并行生成预测。此外，anchor boxes可以进一步处理尺度变化。anchor boxes设计用于将所有可能的实例框的连续空间离散为具有预先设定的位置、比例和纵横比的有限数量的框。instance boxes 通过 IoU 被匹配到 anchor boxes。

One challenging problem for object detection is scale variation. To achieve scale invariability, state-of-the-art detectors construct feature pyramids or multi-level feature towers. And multiple scale levels of feature maps are generating predictions in parallel. Besides, anchor boxes can further handle scale variation. Anchor boxes are designed for discretizing the continuous space of all possible instance boxes into a finite number of boxes with predefined locations, scales and aspect ratios. And instance boxes are matched to anchor boxes based on the Intersection-over-Union (IoU) overlap.

在训练期间，我们动态地将每个 ground-true box 分配给最合适的特征层（这也就是 online feature selection 了）。在推理时，FSAF 模块可以通过并行输出预测与 anchor-based branch 联合工作。

During training, we dynamically select the most suitable level of feature for each instance based on the instance content instead of just the size of instance box. The selected level of feature then learns to detect the assigned instances. At inference, the FSAF module can run independently or jointly with anchor-based branches.

2. 相关工作

Recent object detectors often use feature pyramid or multi-level feature tower as a common structure. SSD first proposed to predict class scores and bounding boxes from multiple feature scales. FPN and DSSD proposed to enhance low-level features with high-level semantic feature maps at all scales. RetinaNet addressed class imbalance issue of multi-level dense detectors with focal loss. DetNet designed a novel backbone network to maintain high spatial resolution in upper pyramid levels. However, they all use pre-defined anchor boxes to encode and decode object instances. Other works address the scale variation differently. Zhu et al enhanced the anchor design for small objects. He et al modeled the bounding box as Gaussian distribution for improved localization.

The idea of anchor-free detection is not new. DenseBox first proposed a unified end-to-end fully convolutional framework that directly predicted bounding boxes. UnitBox proposed an Intersection over Union (IoU) loss function for better box regression. Zhong et al proposed anchor-free region proposal network to find text in various scales, aspect ratios, and orientations. Recently CornerNet proposed to detect an object bounding box as a pair of corners, leading to the best single-shot detector. SFace proposed to integrate the anchor-based method and anchor-free method. However, they still adopt heuristic feature selection strategies.

3. Feature Selective Anchor-Free Module

Without lose of generality, we apply the FSAF module to the state-of-the-art RetinaNet and demonstrate our design from the following aspects:

1. how to create the anchor-free branches in the network (3.1);
2. how to generate supervision signals for anchor-free branches (3.2);
3. how to dynamically select feature level for each instance (3.3);
4. how to jointly train and test anchor-free and anchor-based branches (3.4).

3.1. Network Architecture

Feature Selective Anchor-Free Module for Single-Shot Object Detection

3.2. Ground-truth and Loss

Given an object instance, we know that:

• class label : $k$

• ground truth box coordinates : $b=[x,y,w,h]$, where $(x,y)$ is the center of the box, and $w$, $h$ are box width and height respectively.

• ground truth box 在特征层$P_l$上的投影 projected box：$b_p^l=\left[x_p^l,y_p^l,w_p^l,h_p^l\right]$, i.e. $b_p^l=b/2^l$.

• effective box: $b_e^l=\left[x_e^l,y_e^l,w_e^l,h_e^l\right]={ϵ}_e\cdot b$, i.e. ${ϵ}_e=0.2$.

• ignoring box: $b_i^l=\left[x_i^l,y_i^l,w_i^l,h_i^l\right]={ϵ}_i\cdot b$, i.e. ${ϵ}_e=0.5$.

Classification Output

The instance affects $k$th ground-truth map in three ways

• effective box $b_e^l$ 表示 positive 区域，在图中以白色区域表示。
• ignoring region $(b_i^l-b_e^l)$ 在图中以灰色区域表示，该区域内的像素不参与梯度的反向传播。
• 相邻特征层的ignoring boxes也是ignoring region（如果存在）。

ignoring boxes $b_i^l$ 以外的区域表示 negative 区域，在图中以黑色区域表示，特征图区域用 $0$ 填充。

分类损失采用 Focal Loss：
$$\mathrm{F}\mathrm{L}\left(p_{\mathrm{t}}\right)=-{\alpha }_{\mathrm{t}}{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right),where\alpha =0.25and\gamma =2.0$$
The ground-truth for the classification output is $K$ maps, with each map corresponding to one class. The instance affects $k$th ground-truth map in three ways. First, the effective box $b_e^l$ region is the positive region filled by ones shown as the white box in“car” class map, indicating the existence of the instance. Second, the ignoring box excluding the effective box $(b_i^l-b_e^l)$ is the ignoring region shown as the grey area, which means that the gradients in this area are not propagated back to the network. Third, the ignoring boxes in adjacent feature levels $(b_i^{l-1},b_i^{l+1})$ are also ignoring regions if exists. Note that if the effective boxes of two instances overlap in one level, the smaller instance has higher priority. The rest region of the ground-truth map is the negative (black) area filled by zeros, indicating the absence of objects. Focal loss is applied for supervision with hyperparameters $\alpha =0.25$ and $\gamma =2.0$. The total classification loss of anchor-free branches for an image is the summation of the focal loss over all non-ignoring regions, normalized by the total number of pixels inside all effective box regions.

Box Regression Output

The ground-truth for the regression output are $4$ offset maps agnostic to classes. The instance only affects the $b_e^l$ region on the offset maps. For each pixel location $(i,j)$ inside $b_e^l$, we represent the projected box $b_p^l$ as a 4-dimensional vector ${\mathbf{d}}_{i,j}^l=[d_{t_{i,j}}^l,d_{l_{i,j}}^l,d_{b_{i,j}}^l,d_{r_{i,j}}^l]$, where $d_t^l,d_l^l,d_b^l,d_r^l$ are the distances between the current pixel location $(i,j)$ and the top, left, bottom, and right boundaries of $b_p^l$, respectively. Then the $4$-dimensional vector at $(i,j)$ location across $4$ offset maps is set to ${\mathbf{d}}_{i,j}^l/S$ with each map corresponding to one dimension. $S$ is a normalization constant and we choose $S=4.0$ in this work empirically. Locations outside the effective box are the grey area where gradients are ignored. IoU loss is adopted for optimization. The total regression loss of anchor-free branches for an image is the average of the IoU loss over all effective box regions.

During inference, it is straightforward to decode the predicted boxes from the classification and regression outputs. At each pixel location $(i,j)$, suppose the predicted offsets are $[{\hat{o}}_{t_{i,j}},{\hat{o}}_{l_{i,j}},{\hat{o}}_{b_{i,j}},{\hat{o}}_{r_{i,j}}]$. Then the predicted distances are $S\cdot [{\hat{o}}_{t_{i,j}},{\hat{o}}_{l_{i,j}},{\hat{o}}_{b_{i,j}},{\hat{o}}_{r_{i,j}}]$. And the top-left corner and the bottom-right corner of the predicted projected box are $(i-S{\hat{o}}_{t_{i,j}},j-S{\hat{o}}_{l_{i,j}})$ and $(i+S{\hat{o}}_{b_{i,j}},j+S{\hat{o}}_{r_{i,j}}])$ respectively. We further scale up the projected box by $2^l$ to get the final box in the image plane. The confidence score and class for the box can be decided by the maximum score and the corresponding class of the K-dimensional vector at location $(i,j)$ on the classification output maps.

3.3. Online Feature Selection

The design of the anchor-free branches allows us to learn each instance using the feature of an arbitrary pyramid level $P_l$. To find the optimal feature level, our FSAF module selects the best $P_l$ based on the instance content, instead of the size of instance box as in anchor-based methods.

$$\begin{array}{rl}\text{classification loss}& L_{FL}^I(l)=\frac{1}{N\left(b_e^l\right)}\sum _{i,j\in b_e^l}FL(l,i,j)\\ \text{box regression loss}& L_{IoU}^I(l)=\frac{1}{N\left(b_e^l\right)}\sum _{i,j\in b_e^l}\mathrm{IoU}(l,i,j)\end{array}$$

where $N(b_e^l)$ is the number of pixels inside $b_e^l$ region, and $FL(l,i,j)$, $\mathrm{I}\mathrm{o}\mathrm{U}(l,i,j)$ are the focal loss and $\mathrm{I}\mathrm{o}\mathrm{U}$ loss at location $(i,j)$ on $P_l$ respectively.

下图展示了在线特征选择过程。首先，实例 $I$ 通过特征金字塔的每一层。然后，计算所有anchor-free branch 的总损失，选择总损失最小的学习实例。Finally, the best pyramid level $P_{l\ast }$ yielding the minimal summation of losses is selected to learn the instance, $i.e.$

Figure 6: Online feature selection mechanism. Each instance is passing through all levels of anchor-free branches to compute the averaged classification (focal) loss and regression (IoU) loss over effective regions. Then the level with minimal summation of two losses is selected to set up the supervision signals for that instance.

$$l^{\ast }=\arg \underset{l}{\min }{L}_{FL}^I(l)+L_{IoU}^I(l)$$

For a training batch, features are updated for their correspondingly assigned instances. The intuition is that the selected feature is currently the best to model the instance. Its loss forms a lower bound in the feature space. And by training, we further pull down this lower bound. At the time of inference, we do not need to select the feature because the most suitable level of feature pyramid will naturally output high confidence scores.

为了验证Online Feature Selection的有效性，文章同时对比了heuristic feature selection，该方法就是经典FPN中所采用人工定义方法：
$$l^{\prime }=\lfloor l_0+{\log }_2(\sqrt{wh}/224)\rfloor$$

3.4. Joint Inference and Training

联合推理 joint Inference

achor-free branch 在将置信度分数阈值化 0.05 后，仅解码每个金字塔级别中最多 1k 个得分最高的box predictions。最后通过阈值为 0.5 的 NMS 结合 anchor-based branch 的结果来获得最终的预测结果。

初始化 Initialization

For conv layers in our FSAF module, we initialize the classification layers with bias $-\log ((1-\pi )/\pi )$ and a Gaussian weight filled with $\sigma =0.01$, whereπ specifies that at the beginning of training every pixel location outputs objectness scores around $\pi$. We set $\pi =0.01$ following RetinaNet. All the box regression layers are initialized with bias $b$, and a Gaussian weight filled with $\sigma =0.01$. We use $b=0.1$ in all experiments. The initialization helps stabilize the network learning in the early iterations by preventing large losses.

优化 Optimization

total optimization loss:
$$L^{ab}+\lambda \left(L_{cls}^{af}+L_{reg}^{af}\right)$$
where $L^{ab}$ is the total loss of the original anchor-based RetinaNet, $L_{cls}^{af}$ and $L_{reg}^{af}$ are the total classification and regression losses of anchor-free branches, $\lambda$ controls the weight of the anchor-free branches.

Unless otherwise noted, all models are trained for $90k$ iterations with an initial learning rate of $0.01$, which is divided by $10$ at $60k$ and again at $80k$ iterations. Horizontal image flipping is the only applied data augmentation unless otherwise specified. Weight decay is $0.0001$ and momentum is $0.9$.

4. Experiments

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-e0ndHLJX-1646615835105)(https://gitee.com/yancilin/figures/raw/master/img/1903.0062-11–1.svg)]

5. 总结

• anchor-free 和每个位置有一个正方形 anchor 在形式上可以是等价的，也就是利用 FCN 的结构对 feature map 的每个位置预测一个框（包括位置和类别）。但 anchor-free 仍然是有意义的，我们也可以称之为 anchor-prior-free。这两者虽然形式上等价，但是实际操作中还是有区别的。在 anchor-based 的方法中，虽然每个位置可能只有一个 anchor，但预测的对象是基于这个 anchor 来匹配的，而在 anchor-free 的方法中，通常是基于这个点来匹配的。(此处引用参考博文1)

• anchor-free 分支引入了很多的超参数。从实验结果来看，单独的 anchor-free 分支相对于 anchor-based 分支并没有太多优势。如何设计更好的 anchor-free 分支，使超越论文中的 bagging 策略(anchor-based + anchor-free)呢？(此处引用参考博文2)

• 文章从 feature selection 角度设计了新的 FSAF module 来提升性能，从 loss 角度来看，提升了梯度反向传播的效率，有点类似于 SNIP，只更新特定 scale 内物体对应的梯度，但又和 SNIP 不一样，效率比 SNIP 高。(此处引用参考博文3)

参考博文：

1. 物体检测的轮回: anchor-based 与 anchor-free

2. 论文解读-Feature Selective Anchor-Free Module for Single-Shot Object Detection

3. CVPR2019: FSAF for Single-Shot Object Detection