图像的spatial domain 和 frequency domain 图像压缩

什么是图像的spatial domain(空间域)和frequency domain(频域)？

图像的spatial domain是指图像的颜色空间， 以图像像素直接作为处理为基础。在空间域中(x,y)被认为是二维空间中的一个点，数字图像f(x,y)=color为一个定义在二维空间中的矩形区域上的离散函数。

图像的frequency domain是指以频率为自变量描述图像的特征，可以将一幅图像的像素值在空间上的变化分解为具有不同的振幅、空间频率和相位的简振函数的线性叠加。图像中各种空间频率成分的组成和分布称为 图像频谱。

可以通过某些变换手段如（傅里叶变换，离散余弦变换，小波变换等）在频域下对图像进行处理。因为在频域一些特性比较突出，容易处理。

二者之间的关系：

空间域和频域可以相互转换；对图像施行 二维离散傅立叶变换 或 小波变换 ，可以将图像由空间域转换到频域；通过 对应的反变换 又可转换回空间域图像，即人可以直接识别的图像。

图像频域滤波

二维数字图像的滤波主要分为 空间域滤波 和 频域滤波

空间域滤波： 用各种模板直接与图像进行 卷积运算

频域滤波： 在实现某些图像处理的时候，频域的处理比空间域更简单；对于在空间域上的数字图像，根据 卷积定理 可以通过 傅立叶变换 将 空域卷积滤波 变换为 频域滤波，然后再将频域滤波处理后的图像 反变换 回空间域

图像的频率：灰度值变化剧烈程度的指标，是灰度在平面空间上的梯度。

图像的低频

低频就是颜色缓慢地变化,也就是灰度缓慢地变化,就代表着那是连续渐变的一块区域,这部分就是低频. 对于一幅图像来说，除去高频的就是低频了，也就是边缘以内的内容为低频，而边缘内的内容就是图像的大部分信息，即图像的大致概貌和轮廓，是图像的近似信息。

 图像的低频

高频就是频率变化快.图像中什么时候灰度变化快?就是相邻区域之间灰度相差很大,这就是变化得快.图像中,一个影像与背景的边缘部位,通常会有明显的差别,也就是说变化那条边线那里,灰度变化很快,也即是变化频率高的部位.因此，图像边缘的灰度值变化快，就对应着频率高，即高频显示图像边缘。图像的细节处也是属于灰度值急剧变化的区域，正是因为灰度值的急剧变化，才会出现细节。

另外噪声（即噪点）也是这样,在一个像素所在的位置,之所以是噪点,就是因为它与正常的点颜色不一样了，也就是说该像素点灰度值明显不一样了,也就是灰度有快速地变化了,所以是高频部分，因此有噪声在高频这么一说。

数字图像的二维离散傅立叶变换所得的结果的频域成分如下图所示，左上角是直流成分，变换结果四个角周围对应于低频成分，中央部分对应于高频部分

为了便于观察，常常采取 换位 方法使直流成分出现在窗口的中央（中心化），变换后中心为低频，向外是高频。

在频域，可以很方便的实现 图像的锐化和模糊：

截取频率的低频分量，对其作傅立叶反变换，得到的就是模糊后的图像，即 低通滤波

截取频率的高频分量，对其作傅立叶反变换，得到的就是锐化后的图像，即 高通滤

人眼对高频信息不敏感。

图像压缩

有损压缩

 我们从图像的 rgb 表示开始，然后使用压缩算法对其进行编码这是我们存储在内存中的内容，它更紧凑但 与我们原始的 rgb 表示完全不同，因此压缩方案的一部分还需要定义一个解码组件，将我们数据的存储表示转换为计算机可以渲染为图像的 rgb 格式。jpeg 标准的一部分定义了编码 和解码工作。jpeg 中的一个关键点是最终解码的图像不会与原始未压缩图像相同，这就是为什么我们在管道的压缩部分将其称为有损压缩。我们将故意丢失信息以获得压缩 在百分之五的水平上。

在进行图像压缩是什么信息可以丢弃？

        人眼对亮度的变换比对颜色的变换更敏感，所以JPGE利用这一点。rgb 颜色空间：在对角线上从原点到颜色 255 255 255 你会逐渐得到更亮的颜色， 实际上，这些点之间的确切线定义了所有可能的灰度颜色，它们是亮度的直接度量。

 ycbcr: Y 亮度， cb 和 cr 分量将对颜色进行编码。

压缩原始图像的一种方法是，减少对 cbcr 分量的采样，并保留所有亮度分量。该技术被称为色度下采样或更常见的色度二次采样。

通过将 cb 和 cr 通道上的 2x2 块合并为一种颜色，在二次采样后通常很难看到任何变化，我们在每个颜色通道中留下四分之一的原始数据，将总文件大小缩小 50%，但是和jpeg 图像压缩5%相去甚远。

删除像素都是下采样

以一个不同的视角看待图像

        思考图像的一种方法是将它们视为信号，如果我对图像的特定行进行切片，我有一行像素，每个像素的某个值在 0 到 255 之间。如果我们绘制这些值，我们可以得到一个近似值将图像可视化为信号的信号。允许我们讨论图像中的频率分量。

高频分量对应于像素之间的快速变化，而低频分量对应于像素之间的更平滑变化。

二个关键点

1、如果我选取真实图像的随机部分，那么较低的频率分量很可能该区域中的像素。

2、人类视觉系统通常不太敏感图像中的高频细节。

如何从图像中获取频率分量

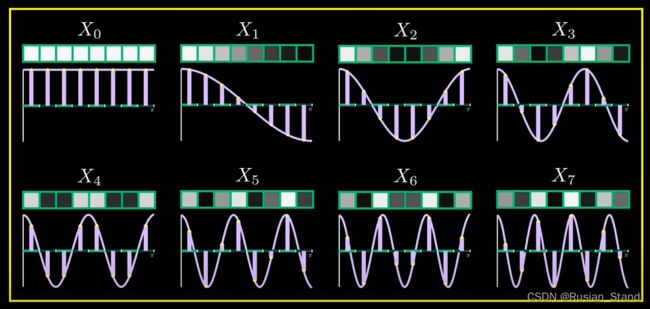
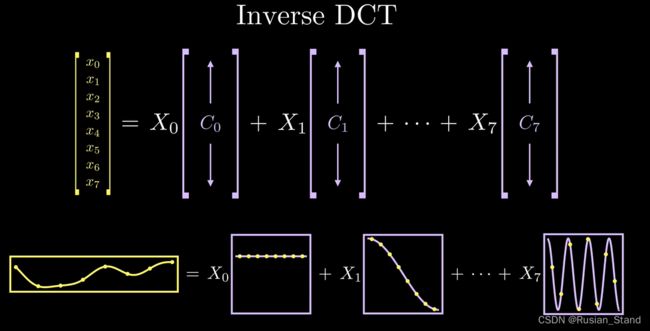
离散余弦变换(DCT), 假设我们只有 8个点，但 dct 的聪明且绝对不明显的想法是将这 8 个点表示为来自余弦波的样本点的总和。dct 从我们的原始信号中获取采样点的输入，并为我们提供与我们将参考的相同大小的输出系数，这些系数表示对原始信号有贡献的不同频率的余弦波的权重。一个很好的类比是将复杂信号分解为简单余弦波的加权和。输出的第一个系数似乎与频率为 1 的余弦波很好地对应，而第二个系数与频率为 2 的余弦波相关。

频率余弦波是什么，它只是一个恒定信号就图像而言，这意味着它为我们提供了一组像素整体亮度的度量，更亮的图像将具有更大的零系数 与较暗的图像相比。

 

jpeg如何 专门使用它

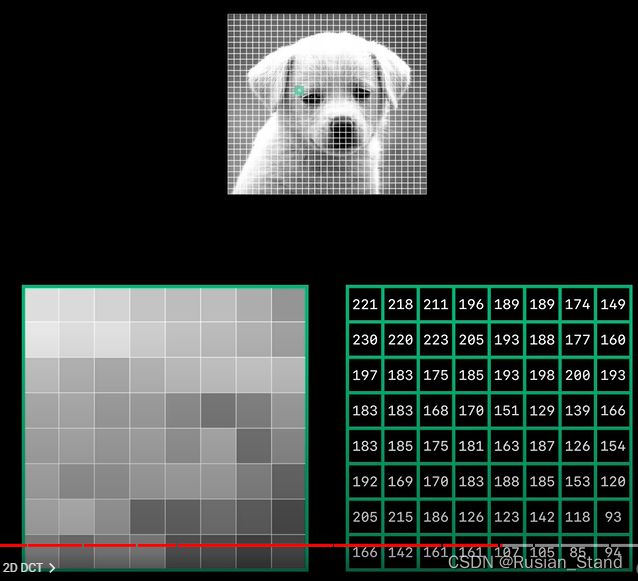
jpeg 获取图像并将其拆分8x8 块。

然后通过减去 128 将它们的值集中在 0 附近。然后我们获取块并将 dct 应用于块的每一行，给我们八组 dct 系数，然后应用 dct 到块的每一列这个过程定义了二维 dct。

 所以最后我们有 64 个系数，每个系数都是在特定的8x8 pattern上。

 注意第一行和第一列对应于早期的一维模式，其他元素是这些模式的组合，就像在一维情况下一样，这里的主要想法是我们可以构建任何 8x8块 使用这 64 种基本模式的图像。但是有一个有趣的现象,合并一小部分系数时，我们的信号和图像已经看起来 非常接近原始图像，再次增加维度，视觉上并没有直观提升效果。

在一个系数之后慢慢建立图像，我们基本上最终得到原始图像的模糊，当我们添加 dct 系数时，慢慢注意到图像开始看起来像原始图像的速度有多快，当我们得到小于 25% 的 dct 系数时，你几乎无法分辨两个图像之间的差异，这证实了jpeg 为何适用于该特定图像的关键方面几乎所有块都由最低频率分量组成，我们通常对高频细节的变化不太敏感。

但下一个自然的问题是我们实际上是如何做到这一点，去掉高频

 

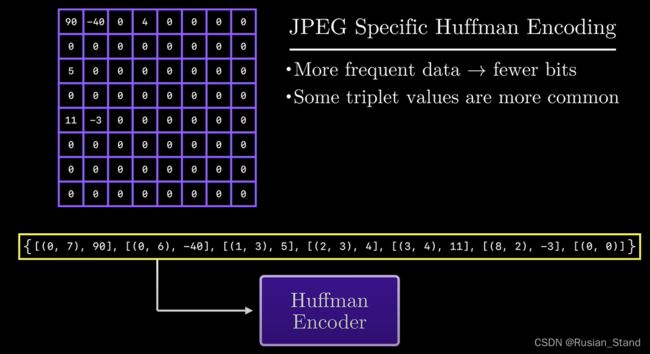
 消除jpeg 中较高频率分量的过程称为量化。量化是一个简单的想法，给定来自 dct 的频率系数的 8x8 矩阵，我们要做的基本上是将每个标量值的元素并将其四舍五入为整数 保留低频，去掉高频，然后运用 长度编码和霍夫曼编码的组合减少存储。

 

 

 

https://www.youtube.com/watch?v=0me3guauqOU

数字图像空间域 频域，深度理解图像变换的原理和过程公式 - 知乎