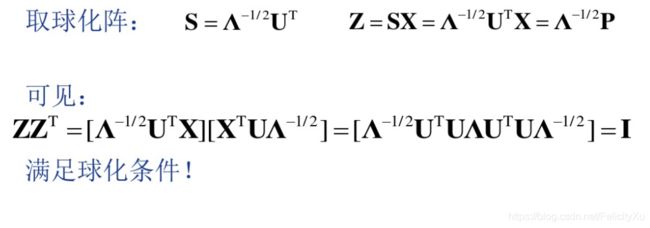独立分量分析（ICA）中遇到的数学概念理解

将找到的相关概念的资料进行了整合，能力有限，理解到位了再用自己的理解写一篇文章。

问题的提出

一、信号和随机变量之间的关系

随机变量（random variable）表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关，都可以数量化，即都能用数量化的方式表达。
例如：某一时间内公共汽车站等车乘客人数，电话交换台在一定时间内收到的呼叫次数，灯泡的寿命等等，都是随机变量的实例。
由随机变量的数据样本点可以估计出随机变量的各阶矩，进而估计出pdf等统计信息。
参考：随机变量百度百科

信号和随机变量之间的关系：
对一个信号X(t):
独立重复试验 —— 抽样ti,i = 1,2…N
样本集 —— { X(ti) }
因此信号X(t)可以看成是一个随机变量，并可估算它的各阶矩，以及谈论它的pdf、独立、相关等统计特性。
例如：

二、独立分量分析法的基本问题

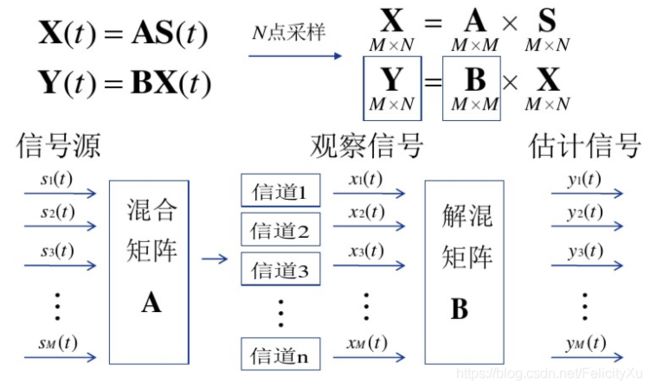
假设源信号由若干个统计上相互独立的信号组成的，他们在空间中形成交叠，独立分量分析是借助多个信道同时观察交叠信号，将观察信号经过解混分解成若干独立成分，作为对源信号的一组估计。

假设：
1、A是线性系统，可用矩阵表示。（实际仿真是随机阵）
2、信道对信号无影响，观察信道数与信号数相同。（ A、B方阵 ）

预备知识

一、统计数学知识

1、概率密度函数

一个函数如果满足如下条件，则可以称为概率密度函数：

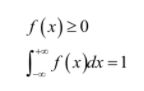
这可以看做是离散型随机变量的推广，积分值为1对应于取各个值的概率之和为1。分布函数是概率密度函数的变上限积分，它定义为：

理解概率密度函数

2、特征函数

特征函数：概率密度函数的连续傅里叶变换的共轭复数，是随机变量的分布的不同表示形式。

如何理解统计中的特征函数？

3、第二特征函数

4、矩

物理意义：
数学中矩的概念来自物理学。在物理学中，矩是表示距离和物理量乘积的物理量，表征物体的空间分布。由其定义，矩通常需要一个参考点（基点或参考系）来定义距离。如力和参考点距离乘积得到的力矩（或扭矩），原则上任何物理量和距离相乘都会产生力矩，质量，电荷分布等。

数学意义：
矩是物体形状识别的重要参数指标。在统计学中，矩表征随机量的分布。如一个“二阶矩”在一维上可测量其“宽度”，在更高阶的维度上由于其使用于橢球的空间分布，我们还可以对点的云结构进行测量和描述。其他矩用来描述诸如与均值的偏差分布情况（偏态），或峰值的分布情况（峰态）

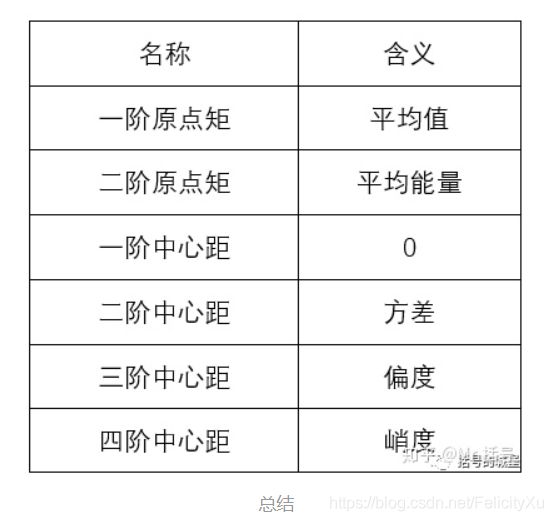
定义在实数域的实函数相对于值c的n阶矩为：

如果点表示概率密度，则第零阶矩表示总概率（即1）,1,2,3阶矩依次为以下三项。数学中的概念与物理学中矩的概念密切相关。

①期望：
随机变量的期望定义为其一阶原点矩：

②方差：
在方差等定义中，期望也成为随机变量的“中心”
随机变量的方差定义为其二阶中心矩：

如何理解概率论中的矩？
概率论中的“矩”是什么意思
概率统计中的矩(离散定义)
概率论中「矩」（moment）的实际含义是什么，高阶矩表示数据的哪些状态？

5、累积量

在概率论和统计学中，一个随机变量的累积量是指一系列能够提供和矩一样的信息的量。累积量和随机变量的矩密切相关。如果两个随机变量的各阶矩都一样，那么它们的累积量也都一样，反之亦然。

对于随机变量X而言，一阶累积量等于期望值E(x)，二阶累积量等于方差V(x)，三阶累积量等于三阶中心矩S(x)，但是四阶以及更高阶的累积量与同阶的中心矩并不相等。在某些理论推导中，使用累积量更加方便。特别是当两个或者更多的随机变量相互独立时，它们的 n阶累积量的和等于它们和的n阶累积量。

累积量-Knowpia百科

二、信息论基本知识

1、熵

熵是某一事情对某人不确定性的度量。一个事情包含多种可能情况，每种情况都具有各自的不确定性(等于确定此事件发生的信息的信息量)。将所有可能情况发生的概率乘以此种情况的不确定性再相加，就得到了这个事情(对某人来说)的平均不确定性，也即是熵。

某种情况发生的概率，等价于一个包含概率倒数种等概率情况的事情发生其中某一特定情况的概率。

结合上面我们所说的信息量，熵也在数值上等于消除某件事情不确定性所需要的平均信息量。在这里，假设某一事情包含N种情况，每种情况以 Xi表示，p(Xi) 代表每种情况发生的概率，那么这件事情的不确定性——熵即为

即熵是信息量的期望。

信号中：

信息论也能如此简单—信息和熵

2、Kullback-Leibier散度

通常在概率和统计中，我们会用更简单的近似分布来代替观察到的数据或复杂的分布。KL散度帮助我们衡量在选择近似值时损失了多少信息。

已知概率分布的熵：

则KL散度只是在上述公式的基础上进行了修改：

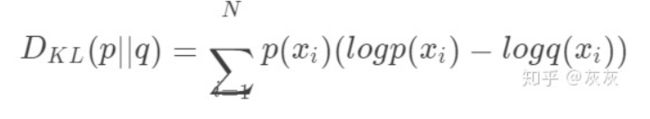
本质上，我们用KL散度看的是对原始分布中的数据概率与近似分布之间的对数差的期望。


Kullback-Leibler(KL)散度介绍

3、互信息

互信息(Mutual Information)是衡量随机变量之间相互依赖程度的度量。
假设存在一个随机变量 X，和另外一个随机变量Y，那么它们的互信息是


什么是互信息？

4、负熵

三、概率密度函数的展开

1、高阶统计量形式

2、非多项式函数的加权和形式

四、信号通过线性系统信息特征的变化

独立分量分析具体算法

对交叠信号X，求解混矩阵B，使Y=BX各分量相互独立。

一、主要步骤

1、预处理部分

对X零均值处理（均值化）

球化分解（白化）

乘以球化矩阵S，使得Z=SX各行正交归一

意义：消除原始各信道数据二阶相关，以后只需要考虑高阶矩量（独立时各阶互累积量为0），简化运算过程。

注：各信道数据不相关≠独立，除非高斯信号。

①PCA 这里就不展开说了

②球化

2、核心算法部分

寻求解混矩阵U（正交变换），使Y=UZ，Y各道数据尽可能独立。（独立判据函数G）

二、各类ICA算法简介

1、批处理算法

2、自适应算法

3、探查性投影寻踪

三、FastICA算法

1、步骤

①输入球化数据Z，经过正交阵某一行向量ui处理（投影），提取出某一独立分量yi。

②将此分量除去，按次序依次提取下去，得到所有的yi以及ui。

2、问题

参考ppt资料：独立分量分析法