强化学习拾遗 —— 强化学习的样本效率

• 总所周知，样本效率低下是强化学习的一个重要问题，本文试图从本质上分析造成这一问题的原因
• 本文仅限于 model-free 方法，不定期更新

因为想申请 CSDN 博客认证需要一定的粉丝量，而我写了五年博客才 700 多粉丝，本文开启关注才可阅读全文，很抱歉影响您的阅读体验

---

1. 强化学习的一般范式

• 强化学习的标准交互过程如下：每个时刻，智能体根据根据其 策略(policy)，在当前所处 状态(state) 选择一个 动作(action)，环境(environment) 对这些动作做出相应的相应的响应，转移到新状态，同时产生一个 奖励信号 (reward)，这通常是一个数值，奖励的折扣累加和称为 收益/回报 (return)，是智能体在动作选择过程中想要最大化的目标
  

• 形式化地讲，一个 general model-free RL framwork 大概会是下面这样

  1. 依照策略（通常是 $ϵ$-greedy）和环境交互，得到轨迹
  2. 计算轨迹收益（MC or TD）
  3. 更新对价值函数的估计
  4. 根据价值函数修正策略（greedy 部分）

  使用流程图表示这个过程
  

• 这个流程中，最重要的就是对价值函数的估计，价值函数是当前对从状态 $s$（状态动作 $(s,a)$） 出发可以得到的期望回报的估计值，代表目前 agent 认为这个状态（状态动作对）有多 “好”。追求高价值的状态和动作，对于智能体实现最大化回报这一目标而言是 “无偏的”，可以把价值函数看做 agent 获得的关于环境的 局部知识，利用它可以直接得到贪心最优动作 ${\mathrm{argmax}}_a{q}_{\pi }(s,a)$，这是对 agent 的一个 局部指导，可以用于构建策略
  

• 再次精炼这个过程，只看最重要的部分，其实强化学习做的事情就是 利用奖励估计策略价值，再根据价值改进策略
  

  这个过程中涉及两个关键环节，其实也对应到 RL 要求解的两个关键问题

  1. Reward (of policy) to Value，如何根据策略 $\pi$ 的奖励估计价值 $v_{\pi },q_{\pi }$，这其实是 prediction 问题
  2. Value to (better) Policy，如何根据价值得到策略，这其实是 control 问题

• 可以剧透一下，我认为导致 Model-free RL 样本效率低下的原因主要有（只想知道结论的话，看完下面这些就可以了）

  1. Reward to Value 基本都是用的蒙特卡洛（MC）及其变形方法，而蒙特卡洛是很慢的，这在学习早期导致 盲目探索（特别是在稀疏奖励的情况下，此问题更加严重）
  2. Reward to Value 过程通常使用基于 Bellman optimal equation 或 Bellman equation 的 TD 更新，在强化学习中使用这种 bootstrap 思想，会导致学习目标（TD target）中的误差不断累积，价值收敛前会多次震荡
  3. Value to Policy 涉及到 “探索-利用” 困境，不佳的探索方法在学习后期导致 片面利用
  4. DRL 方法涉及到神经网络更新，而训练神经网络使用的梯度方法效率很低。特别是 Value to Policy 更新策略网络时，简单的随机梯度下降无法约束策略变化程度，可能导致策略多次震荡

  注意：上述 4 点问题是当前 Model-free RL 方法的本质决定的，是它的 “nature”，不过具体到某个特定方法时不一定同时出现，比如

  1. 前两条都是针对 “要学习价值函数” 的方法而言的，如果使用 MC 思想处理价值则不存在相关问题（如 REINFORCE 方法）
  2. 如果是表格型方法则不存在第 4 点问题
  3. …

  这些问题会相互作用，使得情况变得更糟，比如

  1. 2/4 条相互作用，神经网络（准确地说，任意函数近似方法）的泛化性会导致价值更新相互影响，原本估计得比较准确的位置可能变得不准，提供的 TD target 更不准确
  2. 1/2/3 条相互作用，在 MC 和不准确的 TD target 作用下，agent 学到的价值函数是渐进准确的，在这种基础上做 control 就不得面临 “探索-利用” 困境，agent 会从盲目探索转向片面利用，导致样本效率低下
  3. 4 条中常用的随机梯度下降本质也是一种 MC 方法，和第 1 条呼应上了
  4. …

2. Reward to Value（prediction）

2.1 问题1：无处不在的 MC

• 本节列举一些经典、基础的强化学习方法，意在说明大部分RL方法都在用 MC 及其变体（如 TD）估计价值函数，如果不想看分析过程，可以跳过整个 2.1 节

  这个其实是好理解的，因为价值函数是期望的形式，而我们又没法直接积分求解，只能使用MC及其变体来估计了，MC 的低效是 RL 低效的原因之一

• 先给出几个关键公式

  1. 回报（return）
     $$\begin{array}{rl}{G}_t& \doteq R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ & =R_{t+1}+\gamma [R_{t+2}+\gamma R_{t+3}+...]\\ & =R_{t+1}+\gamma G_{t+1}\end{array}$$
  2. 价值函数（使用不同策略，得到的奖励信号不同，最后获得的收益不同的，价值也不同），策略 $\pi$ 对应的价值函数为
     $$\begin{array}{rl}& q_{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]\\ & v_{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]\end{array}$$
  3. 最优价值函数（也就是最佳策略对应的价值函数）为
     $$\begin{array}{rl}& v_{\ast }(s)\doteq \underset{\pi }{\max }{v}_{\pi }(s)\\ & q_{\ast }(s,a)\doteq \underset{\pi }{\max }{q}_{\pi }(s,a)\end{array}$$

2.1.1 离散环境（表格形方法）

2.1.1.1 Bellman equation DP

• 这个其实是 model-based 方法，即需要知道环境模型的方法，本文主要讨论 model-free 方法，这里放出这个方法主要是为了引入一些概念
• 在 model-based 情况下，要解prediction问题，可以直接反复迭代 bellman equation，这样就能收敛到当前策略下的价值函数。所谓 Bellman equation，其实就是
  $$\begin{array}{r}\begin{array}{rl}{v}_{\pi }(s)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|s]\\ & =\sum _a\pi (a|s)[r(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)v_{\pi }(s^{\prime })]\end{array}\\ \begin{array}{rl}{q}_{\pi }(s,a)& ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|s,a]\\ & =r(s,a)+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)\sum _a\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })\end{array}\end{array}$$ 对于最优价值函数，也有对应的 Bellman optimal equation
  $$\begin{gathered} \begin{array}{rl}{v}_{\ast }(s)& =\underset{a\in \mathcal{A}(s)}{\max }{q}_{{\pi }_{\ast }}(s,a)\\ & =\underset{a}{\max }{\mathbb{E}}_{{\pi }_{\ast }}[G_t|S_t=s,A_t=a]\\ & =\underset{a}{\max }{\mathbb{E}}_{{\pi }_{\ast }}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a]\\ & =\underset{a}{\max }\mathbb{E}[R_{t+1}+\gamma v_{\ast }(S_{t+1})|S_t=s,A_t=a]\\ & =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\ast }(s^{\prime })]\end{array} \\ \begin{array}{rl}{q}_{\ast }(s,a)& =\max {\mathbb{E}}_{{\pi }_{\ast }}[G_t|S_t=s,A_t=a]\\ & =\max {\mathbb{E}}_{{\pi }_{\ast }}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a]\\ & =\mathbb{E}[R_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_{\ast }(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }{q}_{\ast }(s^{\prime },a^{\prime })]\end{array} \end{gathered}$$
• 需要注意的有以下几点
  1. 等式中包含状态转移矩阵 $p(s^{\prime }|s,a)$ 和奖励函数 $r(s,a)$，这些都是环境信息，因此必须要有环境模型（i.e. model-based）
  2. 强化学习中的 reward 信号是和 $(s,a)$ pair 绑定的，Bellman equation 建立了某个策略下，相邻状态/状态动作的价值间的迭代关系，利用它可以将这种局部的指导信号沿着轨迹传递开来

     使用动态规划方法，不断迭代 Bellman equation，就一定能收敛到策略 $\pi$ 对应的价值函数 $v_{\pi }$ 和 $q_{\pi }$，这种 prediction 方法称为 policy evaluation。从数学上讲这属于 “不动点迭代法”，关于价值函数就是 Bellman equation backup 不动点的证明，请参考 强化学习拾遗 —— Bellman 迭代的收敛性

• 基于 Bellman equation DP 的 control 方法有两种
  1. policy iteration：先使用 Bellman equation 迭代得到当前价值 $v_{\pi }$ 和 $q_{\pi }$，然后在每个状态 $s$ 处根据价值贪心地改进策略，从而得到一个更好的（即能获得更多回报的）策略，这个操作称为 policy improvement，反复执行 policy evaluation 和 policy improvement，可以收敛到最优价值函数$q_{\ast }$、$v_{\ast }$ 和最优策略 ${\pi }_{\ast }$
  2. value iteration：直接反复迭代 Bellman optimal equation 至收敛，这样可以直接得到 $v_{\ast }$ 和 $q_{\ast }$，这等价于交替进行 单步policy evaluation 和 policy improvement

2.1.1.2 Monte Marlo (MC)

• 注意到我们要估计的价值函数是一个期望，要做 prediction，一个直接的想法就是使用大量样本的均值来估计价值，这就是蒙特卡洛方法
• 先采集大量轨迹，对其中每个 $s$ 或 $(s,a)$ 开始的轨迹片段计算 return $g_t$，然后就有
  $$\begin{array}{rl}& v_{\pi }(s)=\underset{n\to \infty }{\lim }\frac{1}{n}\sum _{i=1}^{\infty }{g}_t(s)=\mathbb{E}[G_t|S_t=s]\\ & q_{\pi }(s,a)=\underset{n\to \infty }{\lim }\frac{1}{n}\sum _{i=1}^{\infty }{g}_t(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]\end{array}$$ 通常使用增量式更新的方法来计算这个均值
  $$\begin{array}{rl}& v_{\pi }(s)\leftarrow v_{\pi }(s)+\frac{1}{N(s)}(g_t-v_{\pi }(s))\\ & q_{\pi }(s,a)\leftarrow q_{\pi }(s,a)+\frac{1}{N(s,a)}(g_t-q_{\pi }(s,a))\end{array}$$ 其中的计数 $\frac{1}{N}$ 可以使用某个 $\alpha \in [0,1]$ 代替，以适应非平稳情况
• MC 方法的问题在于，必须有完整的轨迹才能计算收益 $g_t={\sum }_{k=0}^T{\gamma }^k{R}_{t+k+1}$，这有时是很难的；一些场景中可能是持续的任务，难以分出episode的概念，这时MC方法就会失效

2.1.1.3 Temporal difference (TD)

• 根据前文分析，有 $G_t=r_{t+1}+\gamma G_{t+1}$，注意价值函数是对期望收益 $\mathbb{E}[G]$ 的估计，这启发我们在做 prediction时，使用当前计算的下一时刻 $s^{\prime }$ 或 $(s^{\prime },a^{\prime })$ 的价值 $v_{\pi }(s^{\prime })$ 或 $q_{\pi }(s^{\prime },a^{\prime })$ 代替 $G_{t+1}$。也就是说

  1. 增量式 MC 中，我们希望 $v_{\pi }(s)$ 和 $q_{\pi }(s,a)$ 靠近 $G_t$
  2. TD 中，我们希望 $v_{\pi }(s)$ 靠近 $r_{t+1}+\gamma v_{\pi }(s^{\prime })$；$q_{\pi }(s,a)$ 靠近 $r_{t+1}+\gamma q_{\pi }(s^{\prime },a^{\prime })$

  这个想法是合理的，以状态价值为例，$v_{\pi }(s)$ 和 $r_{t+1}+\gamma v_{\pi }(s^{\prime })$ 都是当前对真实价值的估计，有 $$\mathbb{E}[v_{\pi }(s)]=\mathbb{E}[r_{t+1}+\gamma v_{\pi }(s^{\prime })]$$ 后者包含一个真实得到的奖励 $r_{t+1}$，因此比纯粹估计更准确一些，应当让估计朝着向它靠近的方向更新，我们称要靠近的目标为 TD target，称更新时的差值为 TD error

• TD 方法的一个关键优势在于，它不需要完整的轨迹，只要一个转移 (transition) $(s,a,r,s^{\prime })$ 就能进行一步更新。我们称收集 transition 的策略为 behavior policy；利用这些 transition 学习价值得到的策略称为 target policy 。类比增量式 MC，价值更新公式如下
  $$\begin{array}{rl}& v_{\pi }(s)\leftarrow v_{\pi }(s)+\alpha [r_{t+1}+\gamma v_{\pi }(s^{\prime })-v_{\pi }(s)]\\ & q_{\pi }(s,a)\leftarrow q_{\pi }(s,a)+\alpha [r_{t+1}+\gamma q_{\pi }(s^{\prime },a^{\prime })-q_{\pi }(s,a)]\end{array}$$ 上面这种更新方式使用策略 $\pi$ 收集 transition， 并用来更新策略 $\pi$ 的价值，其 behavior policy 和 target policy 是相同的，具有这种特性的方法属于 同轨on-policy 方法，直接使用上面这个更新公式做价值估计的算法称为 Sarsa 算法

• behavior policy 和 target policy 也可以设为不同的策略，具有这种特性的方法属于 离轨off-policy 方法。一个重要的 special case 是使用策略 $\pi$ 收集的 transition 来更新最优策略 ${\pi }_{\ast }$ 的价值 $v_{\ast }$ 和 $q_{\ast }$，更新公式如下
  $$\begin{array}{rl}& v_{\pi }(s)\leftarrow v_{\pi }(s)+\alpha [r_{t+1}+\gamma \underset{s^{\prime }}{\max }{v}_{\pi }(s^{\prime })-v_{\pi }(s)]\\ & q_{\pi }(s,a)\leftarrow q_{\pi }(s,a)+\alpha [r_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_{\pi }(s^{\prime },a^{\prime })-q_{\pi }(s,a)]\end{array}$$ 使用此更新公式的方法称为 Q-learning

• TD 方法的本质：一种以匹配 Bellman equation 或 Bellman optimal equation 为目标的非平稳增量式 MC

  1. 上面的TD方法中，我们在更新之前只运行了一步，即从状态 $s$ 转移到 $s^{\prime }$ 后就立即更新，这种方法称为 TD(0)/单步TD；我们也可以在一次更新之前运行多步，这样的方法称作 n步TD，当n越来越大直到 n=horizon 时，TD方法变为MC方法。因此，TD本质是MC的一个变体
     
  2. 对比看 sarsa 和 policy evaluation；Q-learning 和 policy iteration，你会发现 TD 就是在利用 MC 的方式，使价值函数匹配 Bellman Equation 和 Bellman Optimal Equation。以 sarsa 对 $V$ 的评估为例进行说明
     1. 针对非平稳情况的增量式 MC 为：$$v_{\pi }(s)\leftarrow v_{\pi }(s)+\alpha (g_t-v_{\pi }(s)),\alpha \in [0,1]$$ 估计结果为 $$v_{\pi }(s_t)={\mathbb{E}}_{\pi }[g_t]$$
     2. Sarsa 更新公式为 $$v_{\pi }(s)\leftarrow v_{\pi }(s)+\alpha [r_{t+1}+\gamma v_{\pi }(s^{\prime })-v_{\pi }(s)],\alpha \in [0,1]$$ 发现和上面的形式完全相同，估计结果为 $$v_{\pi }(s_t)={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|s]$$ 这正是 Bellman equation，因此 RL 中的 TD 本质就是一种以匹配 Bellman equation 或 Bellman optimal equation 为目标的非平稳增量式 MC

  所以后面我们一旦看到 TD，就要知道这个方法中也使用 MC 思想了

  这里我想补充一点，如果从 agent 获取指导信息的角度来考虑，可以发现 TD 方法的一个重要特点：

  1. 原本环境的指导信号（reward 信号）是仅仅和某个 $(s,a)$ pair 绑定的，agent 只有探索到这个特定的 pair 时才能获取指导，指导信号非常稀疏；引入 TD 的 bootstrap 思想后，任意一个 $(s,a)$ pair 处都得到了即时的指导信号（TD target），这使 agent 得到的指导信号变得稠密
  2. TD 是把双刃剑，在给予更加稠密的指导信号的同时，这些基于当前估计的信号又是不准确的，常常会误导函数近似器（如价值神经网络）的更新方向，有时反而可能导致价值收敛更慢（我觉得如果原本奖励信号就很稠密，可能会出现这种情况），2.2 节会进一步讨论此问题

2.1.2 连续环境（函数近似方法）

• 在 2.1 节的离散环境（即动作空间和状态空间是离散的）中，我们通常使用一些表格来记录所有 $s$ 和 $(s,a)$ 的价值以及策略 $\pi (a|s)$。当环境是连续环境时，动作或状态可以无限细分，这就没法用表格来表示价值和策略了。这时，我们只能使用一个函数来表示价值和策略，并利用神经网络来估计它们，这就引入了价值网络和策略网络，这类方法统称为深度强化学习（DRL）方法

• 使用不同网络架构的 DRL 方法非常多，下图（蓝色方块）涵盖了一些主流方法
  

• 如图所示，所有 Model-Free 方法总体上可以分两类

  1. value based 方法：思想和离散方法一脉相承，就是找到最优的价值网络，得到最优价值，进而得到策略。这类方法的问题有二，一是不能处理连续动作空间；二是在价值上贪心只能找出唯一一个最优动作，无法给出随机策略（可以加 $\epsilon$ 随机试探缓解，但是这种随机策略通常不是最好的）。代表算法是 Deep Q-Learning (DQN)
  2. policy based 方法：这类方法试图直接找出最优的策略网络，不存在上述问题。代表算法是 policy gradient (PG)，

  因为 DRL 方法太多，不可能全部介绍，下面仅简介两类方法的代表算法

2.1.2.1 Deep Q-Learning（DQN）

• DQN 和 Q-Learning 没有太大区别，它也是要做 prediction 去估计 $q_{\ast }$，再利用 $q_{\ast }$ 做 control，只是这里的价值是使用神经网络估计的，通常表示为 $Q(s,a;w)$，其中 $w$ 是网络参数
• 前面 TD 那节 Q-Learning 已经讲了很多，下面直接上公式
  1. TD target：$y_t=r_{t+1}+\gamma {\max }_{a}Q(s^{\prime },a;w_t)$
  2. TD error：${\delta }_t=Q(s_t,a_t;w_t)-y_t$
  3. L2 loss：$L_t=\frac{1}{2}{\delta }_t^2$
  4. gradient：$g_t={▽}_w{L}_t=\frac{\partial L_t}{\partial w}=\frac{\partial L_t}{\partial {\delta }_t}\frac{\partial {\delta }_t}{\partial Q}\frac{\partial Q}{\partial w}={\delta }_t\frac{\partial Q}{\partial w}={\delta }_t{▽}_{w}Q(s_t,a_t;w_t)$
  5. update: $w\leftarrow w-\alpha g_t=w-\alpha {\delta }_t{▽}_{w}Q(s_t,a_t;w_t)$
• 注意我们还是在用 TD 方法估计 $q_{\ast }$ 函数，虽然加了神经网络，但本质依然是 MC

2.1.2.2 policy gradient (PG)

• 这类方法试图使用一个神经网络拟合策略函数 $\pi (a|s)$，通常表示为 $\pi (a|s;\theta )$，其中 $\theta$ 是网络参数。对于离散动作空间，用softmax函数来描述；对于连续的动作空间，用高斯函数来描述（更好的处理方式是 DPG 算法，这里不提）。某种程度上说，这类方法是要跳过显式的 prediction 过程，直接做 control 了

• 注意到状态价值 $v$ 和状态动作价值 $q$ 间的关系
  $$v_{\pi }(s;\theta )={\mathbb{E}}_{A\sim \pi }[Q_{\pi }(s,a)]=\sum _a\pi (a|s;\theta )Q_{\pi }(s,a)$$ 一个好的策略可以得到最多的收益，因此我们的目标就定为最大化总状态价值 $J(\theta )={\mathbb{E}}_S[v(S;\theta )]$

• 要做这个优化，是比较困难的，难度在于求期望时积分不好算

  1. 求 $\frac{\partial V(S;\theta )}{\partial \theta }$，对 $S$ 积分不好做，改成求单个状态 $s$ 的微分 ，使用 MC 方法近似
  2. $\frac{\partial V(s;\theta )}{\partial \theta }={\mathbb{E}}_{A\sim \pi (\cdot |s;\theta )}[\frac{\partial log\pi (A|s;\theta )}{\partial \theta }{Q}_{\pi }(s,A)]$，对 $A$ 积分不好做，改成对单个动作 $a$ 计算微分 ，使用 MC 方法近似
  3. $t$ 时刻，计算状态 $s_t$ 处执行 $a_t$ 的微分 $d_{\theta ,t}=\frac{\partial log\pi (a_t|s_t;\theta )}{\partial \theta }{|}_{\theta ={\theta }_t}$
  4. 梯度 $g(a_t,{\theta }_t)=Q_{\pi }(s_t,a_t)\cdot d_{\theta },t$
  5. update：${\theta }_{t+1}\leftarrow {\theta }_t+\beta \cdot g(a_t;{\theta }_t)$

  现在还剩下一个问题，就是 $Q_{\pi }$ 怎么算

  1. 使用 MC 直接估计，这对应 REINFORCE 算法
  2. 引入另一个价值网络，使用 TD 算法 Sarsa 求解，这对应 Actor-Critc 算法

• 可见，policy gradient 的本质是要最大化总的状态价值 $v$，这个过程用了大量的 MC 和 TD 相关操作，因此它也是基于 MC 的

2.2 问题2：TD target 不准确

• 几乎任何基于 Bellman 公式使用 TD 思想的方法都会遇到此问题，虽然大家都知道 TD target 是不准确的，但是通常对此没有直观的认识，我也是最近看了 DisCor 的论文后才意识到此问题的重要性，加上了这一段
• 这里就简单说明一下：一般 RL 的设定下，agent 执行一个 $(s,a)$ 不但影响即时 reward，而且也会影响下一个时刻的 reward 和状态，任意一个 $(s,a)$ 的 reward 不仅和自身的 $Q$ 价值绑定，还会影响其他状态的价值估计，这就导致最终的价值估计和策略有关，而学习过程中的策略又是非平稳的，学习样本不可能来自 ${\pi }^{\ast }$，因此价值估计时使用的样本也不可能是来自 $Q^{\ast }$ 的 i.i.d 采样。也就是说，使用 bootstrap 技巧得到的优化目标 TD target 虽然是 “即时的”，但不同于普通监督学习，这里训练使用的样本标记是基于当前估计构造的，而不是来自 ground truth 的 i.i.d 采样，这样我们的学习目标就出现了偏差
• 当引入函数近似时，上述问题更加严重，我们知道函数近似方法有两个特点：“计算越多的位置越准确” 和 “有相似特征的位置会受到泛化性影响”，看以下示例
  
  这是一个有 7 个状态的树状 MDP，agent 从根状态出发（最上面）向叶子状态（最下面）移动。其中形状一样的状态有相似的特征，每张图的虚线框表明了该轮更新时使用的交互轨迹（on-policy 设定），状态颜色越绿说明其价值估计越准确，越红则越不准确。从图中可以发现优化过程出现多次震荡（由于当前轨迹更新时使用不准确的 TD target 以及对相似状态状态的泛化性，打圈部分原本估计较好的状态估计又变坏了），仔细来看有以下三点
  1. 叶子状态：访问（采样计算）较少，Bellman optimal equation 符合性较差，（使用函数近似时）拟合较差，由于在轨迹尾部，这会提供有较大误差的 TD target
  2. 根状态：访问（采样计算）较多，Bellman optimal equation 符合性较好，（使用函数近似时）拟合较好，学到了误差很大的 TD target
  3. 使用函数近似时，具有相似特征的状态在更新时互相影响（有可能原本在叶子处一个误差较小的状态，受到根部状态更新时的泛化影响后误差变大了，进而其提供的 TD target 也变差了）
• TD target 不准确导致 RL 学习价值函数时缺少 “纠正性反馈”，价值估计收敛过程中很可能出现大量震荡导致样本效率低下，甚至出现次优收敛等问题。关于此问题更详细的说明和解决方法可以参考：论文理解【RL - Exp Replay】—— 【DisCor】Corrective Feedback in RL via Distribution Correction

3. Value to Policy (control)

3.1 问题3：探索-利用困境

• “探索-利用困境” 是 control 部分一个老生常谈的问题，先简单说明一下。如果我们持续对动作价值进行估计，那么任一时刻都会至少有一个动作的估计价值是最高的，我们将这些对应最高估计价值的动作成为 贪心动作。在选择动作时，有两种选择

  1. 利用/开发：利用当前所知的关于动作价值的知识，从贪心动作中选择一个执行
  2. 试探/探索：选择某个非贪心动作执行

  显然，“开发” 可以最大化当前时刻的期望收益，但是“试探” 有助于我们更准确地估计当前非贪心动作的价值，进而找到真正的最优动作，合理地 “试探” 从长远来看可能带来总体收益的最大化。注意，同一次动作选择时，开发和试探是不可能同时进行的，这就要求我们在开发和试探间进行平衡

• 为了得到一个好的策略，贪心地 “利用” 的成分是必不可少的。一个极端的例子是 MC policy iteration，这种算法使用 MC 替代 policy iteration 中的 policy evaluation（prediction） 步骤，相当于把开发和探索分开，为了得到最优策略，必须有 policy improvement 这一步。问题在于，我们难以把握应该在探索到什么程度之后进行利用，这往往导致 “学习后期片面利用” 的问题，使得样本效率低下

• 事实上，探索-利用困境是一个 human-level 的问题，只要用于决策的依据是渐进准确的，那么该问题必然出现（回忆一下你去探索新餐馆却踩雷的经历吧），理解这一点也给我们带来一个新视角，想想我们是如何在缺失自身经验的情况下做决策的，比如收集别人的评价、观察别人的行为、依赖过去的相似经验、想象可能发生的种种后果等，诶呀，RL 中也有很多方法有这些思想的影子啊！比如模仿学习、又或者 model-free 中的 “规划”、甚至一些对环境建模的 model-based 方法（如 dream to control）

  note：如果仅考虑探索的角度，学界目前也已提出了很多更高级的探索方法，请参考 Lil’log: Exploration Strategies in Deep Reinforcement Learning 这是 OpenAI 研究员 Lilian Weng 的博客，写的非常好，还会经常 update，在此安利一波

3.2 问题4：神经网络的梯度更新

• 首先随机梯度下降很慢应该不用说明了，它能在工程上得到广泛的应用，主要是得益于其普适性强、实现简单等优点。这一节主要说一下使用梯度方法优化策略网络时导致的特殊问题

  note：处理连续控制问题时需要训练策略网络，通常会遇到此问题

• 首先回顾一下 2.1.2.2 节介绍的策略梯度方法（PG），其优化目标是最大化总价值
  $$J(\theta )={\mathbb{E}}_S\left[{\mathbb{E}}_{A\sim \pi (\cdot \mid S;\mathbf{\theta })}\left[Q_{\pi }(S,A)\right]\right]$$ 求梯度有
  $$\frac{\partial J(\mathbf{\theta })}{\partial \mathbf{\theta }}={\mathbb{E}}_S\left[{\mathbb{E}}_{A\sim \pi (\cdot \mid S;\mathbf{\theta })}\left[\frac{\partial \ln \pi (A\mid S;\mathbf{\theta })}{\partial \mathbf{\theta }}\cdot Q_{\pi }(S,A)\right]\right]$$ 注意到这里要对状态空间和动作空间积分，直接是没法做的，很多方法中都是按一般套路使用随机梯度下降法处理，如 AC/A2C/REINFORCE 等。假设 $g$ 是某轮迭代中计算的梯度或随机梯度值，策略网络参数 $\theta$ 会如下更新
  $$\theta \leftarrow \theta +\alpha g$$其中 $\alpha$ 是学习率。这看起来很好，但问题在于强化学习对于策略是非常敏感的，$\pi$ 的一点点变化，都可能导致巨大的性能差异，上面这种更新方式可以通过调整 $\alpha$ 很好地控制参数 $\theta$ 的变化，但无法准确且线性地控制经过神经网络后得到的策略 $\pi (a|s;\theta )$ 的变化，所以梯度优化时很容易 overstep，学到的策略 $\pi (a|s;\theta )$ 在 sweet point 附近反复震荡，收敛缓慢，样本效率低下

• 解决 Policy gradient 方法问题的一个思路是直接换一种优化方法，以回避上面的更新过程，比如改用置信域优化方法

  • 置信域优化是一种经典优化方法，其出发点是：如果对目标函数 $J(\theta )$ 进行优化过于困难，不妨在 $\theta$ 的当前值 ${\theta }_{now}$ 附近构造一个局部范围内和 $J(\theta )$ 十分相似的替代函数 $L(\theta |{\theta }_{now})$，通过在这个局部范围内最优化 $L(\theta |{\theta }_{now})$ 来更新一次 $\theta$ 值，反复迭代上述过程直到收敛。注意到这里的置信域半径控制着每一轮迭代中 $\theta$ 变化的上限，我们通常会让这个半径随优化过程不断减小来避免 overstep，其一步更新和优化过程示意图如下
    
  • 注意到每一轮迭代中，我们都在构造并求解一个小的约束优化问题，这样就不要做 $\theta \leftarrow \theta +\alpha g$ 形式的更新了，更重要的是，我们可以更自由地设计置信域约束条件，从而对每轮迭代中 $\pi (a|s;\theta )$ 的变化进行直接控制

• 把置信域优化方法和 policy based 方法相结合就得到了 TRPO 方法，下面做一些公式推导。记住我们的优化目标是最大化 $J(\theta )={\mathbb{E}}_S[V_{\pi (a|s;\theta )}(S)]$，为了构造 $L(\theta |{\theta }_{now})$，把 ${\theta }_{now}$ 引入 $V_{\pi }(s)$ 中
  $$\begin{array}{rl}{V}_{\pi }(s)& =\sum _a\pi (a|s;\theta )\cdot Q_{\pi }(s,a)\\ & =\sum _a\pi (a|s;{\theta }_{now})\cdot \frac{\pi (a|s;\theta )}{\pi (a|s;{\theta }_{now})}\cdot Q_{\pi }(s,a)\\ & ={\mathbb{E}}_{A\sim \pi (a|s;{\theta }_{now})}[\frac{\pi (a|s;\theta )}{\pi (a|s;{\theta }_{now})}\cdot Q_{\pi }(s,a)]\end{array}$$这样优化目标就变成
  $$\begin{array}{rl}J(\theta )& ={\mathbb{E}}_S[V_{\pi (a|s;\theta )}(S)]\\ & ={\mathbb{E}}_S\left[{\mathbb{E}}_A\right[\frac{\pi (a|s;\theta )}{\pi (a|s;{\theta }_{now})}\cdot Q_{\pi }(s,a)\left]\right]\\ & ={\mathbb{E}}_{S,A}[\frac{\pi (a|s;\theta )}{\pi (a|s;{\theta }_{now})}\cdot Q_{\pi }(s,a)]\end{array}$$ 注意到这个原始优化目标中有两个不好处理的点

  1. 要对动作空间 $\mathcal{A}$ 和状态空间 $\mathcal{S}$ 做积分，这个积分没法做。我们利用 MC 的思想构造替代优化目标，先用 $\pi (a|s;{\theta }_{now})$ 交互得到一批具体的 transition 数据，再用它们 $\frac{\pi (a|s;\theta )}{\pi (a|s;{\theta }_{now})}\cdot Q_{\pi }(s,a)$ 的均值代替期望
  2. 要估计优化得到的 $\pi (a|s;\theta )$ 下的 $Q$ 价值。我们认为置信域内 $Q_{\pi (a|s;{\theta }_{now})}$ 是 $Q_{\pi (a|s;\theta )}$ 的近似，而每个 $(s,a)$ 在其轨迹中的具体 return $g$ 又是 $Q_{\pi (a|s;{\theta }_{now})}$ 的近似，这样就可以用 $g$ 估计 $Q_{\pi (a|s;\theta )}(s,a)$

  解决两个问题后构造出的替代目标函数 $L(\theta |{\theta }_{now})$ 如下：
  $$L(\theta |{\theta }_{now})=\frac{1}{n}\sum _{i=1}^n\frac{\pi (a_i|s_i;\theta )}{\pi (a_i|s_i;{\theta }_{now})}\cdot g_i$$再加上置信域约束，每轮迭代中构造出的约束优化问题为
  $${\theta }_{new}\leftarrow \arg \underset{\theta }{\max }L(\theta |{\theta }_{now})\text{s.t.}\theta \in \mathcal{N}({\theta }_{now})$$为了避免策略的 overstep 问题，直接把更新前后的策略差异的约束作为 $\theta$ 的约束条件，即
  $$\theta \in \mathcal{N}({\theta }_{now})\Rightarrow \frac{1}{n}\sum _{i=1}^n\text{KL}[\pi (a|s;{\theta }_{now}||\pi (a|s;\theta ))]<△$$持续迭代求解上述约束优化问题直至策略收敛的方法就是 TRPO，该方法的一个经典改进是 PPO 方法，其至今也是 model-free RL 的主流方法之一

4. Experiment

• 下面通过一个简单的实验来说明上述的前三个问题如何影响样本效率
• 使用离散环境下经典的 TD 算法 Q-learning，配合最普通的 $\epsilon$-greedy 探索策略进行实验。根据前文说明，这种设定可以作为 general vanilla model-free RL 框架的一个代表，可以用来研究一般 model-free RL 框架的特性

  note：这里用的是表格型方法，不会出现问题4

4.1 实验设定

• 这是一个 15 x 15 的 GridWorld 环境，每个方格是一个状态，agent 可以执行上下左右四个动作，并确定性地转移到相邻状态，起点在左上角，终点在右下角。在终点处可以获得 25 的奖励，其他动作都没有奖励，奖励折扣设为 $\gamma =0.9$，为了最大化奖励，agent 要尽快到达终点以减少衰减
• 使用 value iteration 计算各状态价值，通过颜色显示如下
  
  在本环境设定下，对于非终止状态，贪心策略为
  $$\begin{array}{rl}\pi (s)& =\underset{a}{\mathrm{argmax}}{\mathbb{E}}_{\pi }[r+\gamma v_{\pi }(s^{\prime })|s,a]\\ & =\underset{a}{\mathrm{argmax}}(r+\gamma v_{\pi }(s^{\prime }|s,a))\\ & =\underset{a}{\mathrm{argmax}}{v}_{\pi }(s^{\prime }|s,a)\end{array}$$可见这种确定性情况下的最优策略就是向高奖励状态移动，故在各个状态向右下行动的策略是最优的，从起始状态开始，依照最优策略 ${\pi }_{\ast }$ 行动的所有可能转移使用红直线显示

4.2 实验结果

• 随机试探概率设为 $\epsilon =0.2$，Q-learning 算法，实验结果如下
  

4.3 结果分析

4.3.1 RL 低效的体现：钟型样本效率曲线

• 为了便于讨论，我先定义一个 有效转移 的概念，前文 2.1.3 节已经说明，TD 算法中 TD error 代表对价值估计的更新强度
  $$\begin{array}{rl}& {\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)\\ & {\delta }_t=R_{t+1}+\gamma q(S_{t+1},A_{t+1})-q(S_t,A_t)\end{array}$$ 对于更新价值时有 ${\delta }_t\ne 0$ 的转移，称其为有效转移，它们是对价值估计有所贡献的转移四元组，TD error 代表了贡献的大小。随着有效转移不断发生，局部价值函数估计得越来越好，这就形成了 “局部知识”，可以对 agent 动作给出一定的 “局部指导”，允许 agent 执行更有针对性的探索

  note：本节分析中忽略了问题2，认为每轮迭代后越靠近 TD target 就越好

• 某个转移 “有效” 代表着当前估计价值 $V(S_t)$ 和 TD target $R_{t+1}+\gamma V(S_{t+1})$ 之间还有偏差，这个偏差同时来自于即刻奖励和下一步价值估计。假设价值初始化为 0，在价值估计收敛前，有效转移有两个来源
  1. 可以获得奖励的状态：这些位置即刻奖励 $R_{t+1}>0$，因为估计价值初始化为 0，这导致了最初的有效转移
  2. 不能得到奖励的状态：这些位置没有即刻奖励，TD error 完全来自于 MC 过程中估计的渐进准确特性，这些有效转移是跟随上一种出现的，它们使得价值估计逐步收敛
• 观察上面动图显示的价值函数的学习过程，可以发现，对于一般的 TD 方法，从价值初始化为 0 开始
  1. 价值是从有奖励的状态开始，按轨迹逐步反向转递到前驱状态上的。由于本质是 MC 方法，需要大量样本来近似价值，价值估计速度很慢，某个状态的价值需要多次使用相关的有效转移进行计算才能比较准确
  2. 学习早期：除了有奖励位置，要想在无奖励状态处进行有效转移以更新价值，必须保证 $\gamma V(S_{t+1}))\ne V(S_t)$，由于价值估计速度很慢，所以早期的大部分状态都是 $V(s)=0$ 的，有效转移很少，agent难以获取局部指导，只能 盲目转移，样本效率低下
  3. 学习中期：随着价值逐步 “传递” 到状态上，agent 获取的局部知识越来越多，这又导致了更有方向性的探索，二者相互促进使得样本效率相对提升
  4. 学习后期：由于未探索区域价值仍然是0，在 $\epsilon$-greedy 探索时，agent绝大多数时间会去执行 $V(s)>0$ 的那些状态的相关的转移，使其价值估计得到 “巩固”，所以这实际上又限制了 agent 的探索范围，容易陷入局部最优。随着 “巩固” 过程进行，最后这些状态的价值估计基本收敛到 $\gamma V(S_{t+1}))=V(S_t)$，$\delta =0$，又变成无效转移，agent 片面利用 局部知识，样本效率再次变低
• 总的来说，样本效率是一个 “低-高-低” 的变化规律，形如下面的钟形曲线所示
  
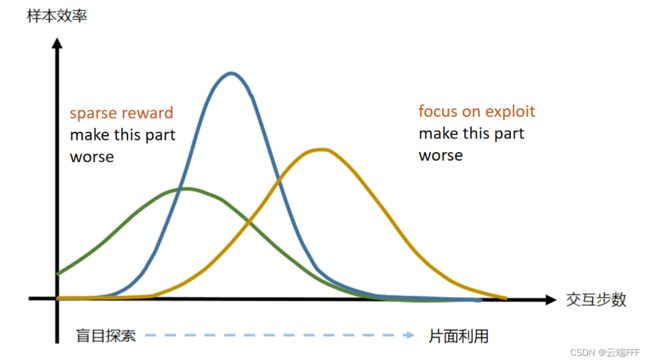
  实验说明，General Model-free RL 没法让样本效率维持在高位，确实有样本效率低的问题
• 对于一些极端情况，问题会更加严重
  1. 见下面左图：奖励信号稀疏时，agent 会被困在盲目探索阶段更长时间。最极端情况下钟形曲线的左侧效率约为 0 的部分无限延长，所有探索交互全部无效，这被称为 稀疏奖励问题
  2. 见下面右图：如果策略过于偏向 “利用”，则学习曲线后期的下降段会非常陡峭
     

4.3.2 RL 低效的原因：General Model-free RL 框架的固有问题

• 综合前文所述，RL 低效的原因主要有四个

  1. prediction 阶段基于 MC 的价值函数更新方法效率低下
  2. TD target 不准确，价值网络训练缺乏纠正性反馈，价值收敛慢
  3. control 阶段 “探索-利用困境”，难以设计一个好的探索策略
  4. 训练神经网络时 gradient-based 方法效率低，且用于 policy network 时容易震荡

• 分析这些问题，会发现它们和强化学习最基础的 MDP 框架是紧密联系的

  1. 用离散的奖励信号估计收益的期望，那肯定要做类似MC的操作
  2. 强化学习中延时奖励的特点迫使我们使用 TD 方法构造即时反馈，MDP 的马尔科夫性质又使得 TD target 不可能准确
  3. 由于决策时依赖的价值估计是渐进准确的，探索-利用困境必然发生
  4. 涉及连续控制问题时必须引入函数估计器，而 NN + gradient-based 优化方法是目前最流行且最强大的函数估计器

• 在现有的基础上修改，上述问题大都只能缓解而无法根治

4.3.3 各种提升样本效率的方法

• 上一节中的问题 2 和 4 相对独立，对应的章节中也较具体地给出了处理措施（这两个是我最近看论文后加的）

  1. 对于问题 2，参考 DisCor 论文：论文理解【RL - Exp Replay】—— 【DisCor】Corrective Feedback in RL via Distribution Correction
  2. 对于问题 4，参考 TPRO/PPO 论文

• 问题 1 和 3 的互相作用比较紧密，它们导致 agent 从盲目探索转向片面利用，可以把 RL 交互过程表示为下图，针对各环节问题，使用橘黄色字标注了一些处理方法，具体不展开说明了
  
  再放一张图片配合总结下（这是我之前一个 presentation 的 PPT，以后可能会讲一下发 B 站）
  

• 最后跳出一般 model-free RL 的框架打开思路看看

  1. 我们可以不要奖励函数而是使用其他方式向 agent 传递目标，这样就能回避掉问题 1 和 问题 2。关于这个请参考：强化学习拾遗 —— 再看奖励函数 第4节
  2. off-policy 性质对于样本效率的影响非常大，model-based 方法其实是 off-policy 性质最强的，也是样本效率最高的方法。对于一些规则清晰容易模拟的环境（如棋牌游戏），直接做个蒙特卡洛树搜索甚至不需要样本了
     
     想一想如何能把 model-free 方法的 off-policy 性质提升

4.4 补充实验

• 针对片面探索的问题，下面展示两个最简单的缓解方法
  1. 使用非平稳 $\epsilon$-greedy 探索策略，下图显示 1000 episodes，随机动作概率 $\epsilon$ 从1均匀下降到0。这种方法可以在早期探索尽量多的区域，并在片面探索发生之前完成价值传递
     
     可见，早期随机概率较大，价值的扩展类似 BFS；后期随机概率减少，价值的扩展过程类似 DFS，其中原由你应该可以看穿了
  2. 增加一个 experience replay buffer，对于 off-policy 方法，可以把过去发生的转移四元组拿出来重复计算。早期的盲目探索阶段我们收集了很多转移，由于价值尚未传播开，当时看来可能很多转移都是 TD error 为 0，但随着价值估计逐渐准确，许多相同的转移对应的 TD error 很可能不为 0 了。 下图显示 500 episodes，每两个 step 间利用 replay 数据更新 5 次
     
     注意右上角有一块区域仍然没有估计到价值，说明 replay buffer 中没有收集到那部分的相关转移。由于 replay 数据是随机抽取的，价值更新位置显得比较随机

     经验重放的一个改进方法是优先经验重放，其核心思想是 agent 在不同 transition 上的 “学习量” 不同，可以通过强调某些 transition 样本提升学习效率，目前大概有三个方向

     1. 强调 TD error 大的 transition，代表方法 PER，请参考：论文理解【RL - Exp Replay】 —— 【PER】Prioritized Experience Replay
     2. 强调 On-policy 性质强的样本，代表方法 LFIW，请参考：论文理解【RL - Exp Replay】—— 【LFIW】Experience Replay with Likelihood-free Importance Weights
     3. 强调 Q value 估计更准确的样本，代表方法 DisCor，请参考：论文理解【RL - Exp Replay】—— 【DisCor】Corrective Feedback in RL via Distribution Correction