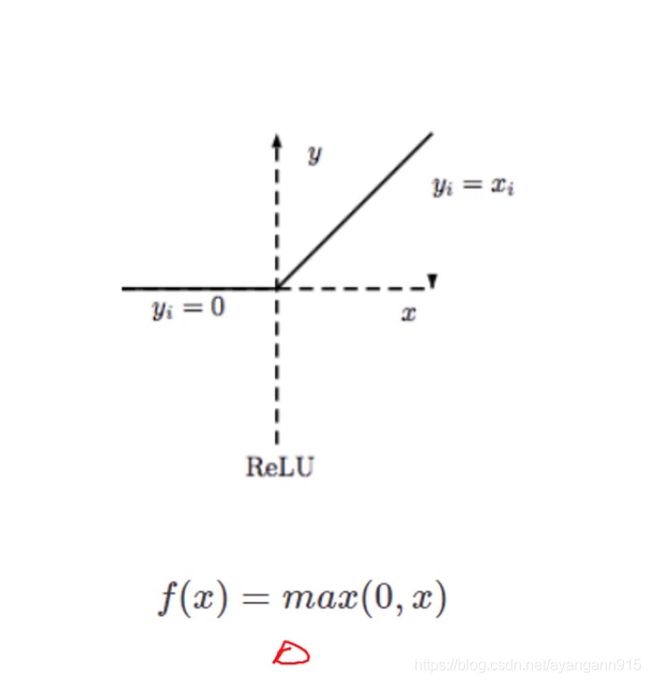002卷积神经网络基础知识
卷积神经网络基础知识
文章目录
-
- 卷积神经网络基础知识
-
- 卷积神经网的基本定义
- 卷积神经网的基本网络结构单元
-
- 卷积(卷积层)
-
- - 定义
- -重要参数
- 卷积的定义和使用
- 池化(池化层)
-
- -池化
- -最大池化:
- 常见池化策略
- 激活函数(激活层)
-
- Sigmoid
- Tanh
- ReLU
- BathchNorm层
-
- BatchNorm层的使用
- 全连接层
- Dropout
- 损失层
-
- 损失函数:
- 损失层
- 交叉熵损失实现
- 回归任务L1,L2,Smooth L1损失
- 卷积神经网的介绍
-
- LeNet
- AlexNet
- ZFNet
-
- ZFNet与特征可视化
- VGGNet
- GoogleNet/Inception v1
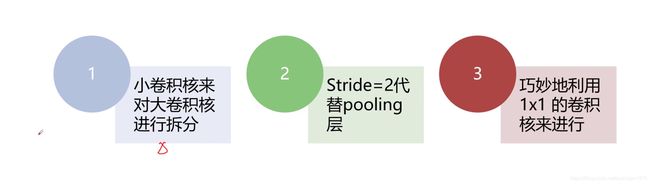
- 从卷积的角度思量,如何减小网络中的计算量
-
- ResNet

卷积神经网的基本定义
- 以卷积结构为主(主干层,还包括池化层等),搭建起来的深度网络(主要解决图片问题,如图像的目标检测)
- 将图片作为网络的输入(输入数据结构,n * w * h * c ),自动提取特征(参数优化的过程),并且对图片的变形(如平移、比例缩放、倾斜)等具有高度不变形。(在进行变形后仍能识别出为人脸)
卷积神经网的基本网络结构单元
- 卷积
- 池化
- 激活
- BN(Batchnorm)
- LOSS(优化)
- 其他层
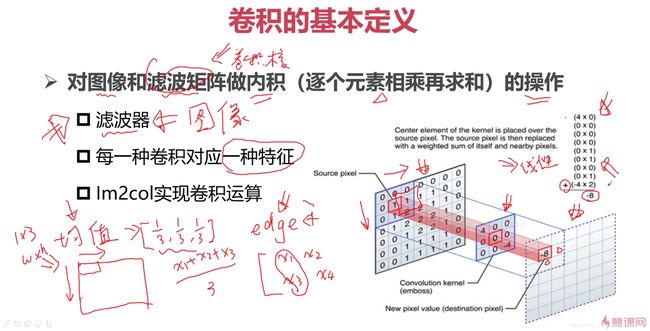
卷积(卷积层)
- 定义
-
滤波器(将卷积理解成滤波器)
均值滤波器去图像噪声:[1/3,1/3,1/3],对图像从左到右,从上到下扫描,取同滤波器一样的窗口(1*3),当前窗口同滤波器进行内积操作,(x1+x2+x3)/3
-
边缘提取:每一种卷积对应一种特征
差异越大边缘越明显,梯度幅值越大
-
Im2col实现卷积运算
每一种卷积核对应一种图像特征,卷积的结果是小窗口中心点的值,继续滑动,得到后续值,最后无法计算的部分用0填充。
https://blog.csdn.net/weixin_43430243/article/details/89512069
-重要参数
-
卷积核
-
图像处理中最常用的是2D卷积核(k_w*k_h)(也有1D卷积,3D卷积)
线性计算:1 * 1=(1 * n)*(n * 1)
-
权重和偏置项:y=w*x+b, b为偏置项
-
常用卷积核:1x1,3x3,5x5
- 保护位置信息,找到卷积之后的点同原始图像的点的对应情况
- padding时对称,填充的时候,奇数卷积核使用padding保证对称性
-
-
卷积------权值共享与局部连接(局部感受野/局部感知)
-
卷积运算作用在局部,如3x3的卷积核,选择3x3的局部范围得到卷积点,整幅图提取不同的范围进行卷积得到最终的卷积图,卷积的3x3的区域对应的就是3x3的感受野
-
Feature map使用同一个卷积核运算后得到一种特征
- 使用同一个卷积核,即在对图像的局部区域进行卷积的时候,我们实际上是通过同一个卷积核进行操作,每一个局部区域对应的卷积核的参数对应的权值是相同的
- 如果当前卷积核用于边缘提取,对图像卷积运算之后,得到的新的特征图就是一种边缘特征
- 如果卷积核完成均值运算,拿到的特征图就是图像均匀或降噪之后的进行均值滤波处理的特征
- 一个卷积核对应一种特征,一种特征就是我们输出的一个Feature map
-
多种特征采用多个卷积核(channel),numout输出的就是需要的卷积核数量
-
权值共享:一个卷积在进行运算的时候对应一个局部区域,对于一幅图像,在进行卷积运算的时候,所有的局部区域对应的卷积核的参数是相同的,将其定义为这些局部区域权值共享
-
局部连接:将卷积网络层和层的关系来看,输入层和输出层就是局部连接
-
-
卷积核与感受野
-
卷积的3x3的区域对应的就是3x3的感受野,卷积核越大,感受野越大,感知到的区域信息越多,能学习到的信息越多,但卷积核越大,参数量越大,模型更复杂,计算量大
5x5卷积运算后输出3x3,再对3x3区域再次卷积,得到1x1,即两个3x3=一个5x5
卷积输出:3x3: nxn——>(n-2)x(n-2)
5x5:nxn——>(n-4)x(n-4)
7x7:nxn——>(n-6)x(n-6)
1x1
-
卷积核
参数量越大,模型越复杂,占用的资源越多,要尽可能减少参数量
计算量决定了算法效率和平台功耗
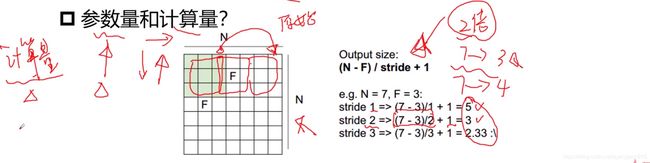
参数量和计算量的计算:
- w:卷积的大小,k_w * k_h,一个2D的卷积对应输入层的一个feature map上,会对原始图像的多个feature map进行卷积,卷积核的大小乘上输入的feature map的数量channel,对所有的feature map进行完一次卷积运算之后,加上偏置项。进行卷积时,是对输入层的特征图的feature map运算时是连通道一起进行卷积的,最后要乘以通道数量In_channel,得到一个feature map,要得到所有feature map需要乘以输出的Out_channel
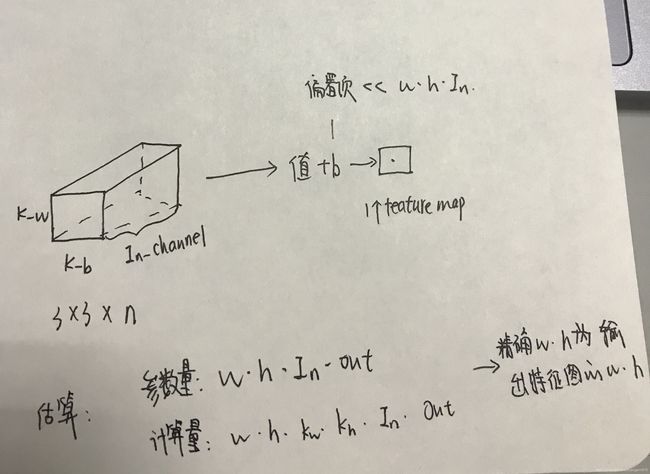
计算量:
需要对整幅图像进行运算,乘以ln_w和ln_h,即输入图像的大小
-
步长(stride)
卷积时对图像从左到右从上到下运算,步长就是运算时上下左右移动取的间隔
stride=1:正常的卷积
stride=2:移动两步,原始图像设置不同的stride(2)就会下采样两倍,图像就是padding之后的两倍
stride>1,进行卷积的次数减少,feature map大小变小,减少计算量,弊端是采样时会损失信息,要考虑代价和收益,如果平衡则可以增加步长
改变stride会影响输出特征图的大小,计算量发生变化,输入的不是原始图像的w和h,而是输出图的w和h
改变stride对参数量量没有影响
-
Pad:确保feature map整数倍变化,对尺度相关的任务尤为重要
如8x8通过3x3的卷积核最终得到6x6的feature map,8x8到6x6的变化不是整数倍的变化,导致点与点之间对应关系模糊,对尺度相关的任务如目标检测,如果不是整数倍变化,计算会存在误差,因为图像上的坐标都是整数,所以要对坐标取整,使用Pad填充,保证整数倍变化

3x3的卷积核:中心点的四周边缘pad 1
5x5的卷积核:pad 2区域
7x7的卷积核:pad 3区域
Pad之后参数量不会变化,但计算量会变化,因为输出特征图的大小变化,计算量不是整数倍变化
卷积的定义和使用
池化(池化层)
-池化
池化,即对输入的特征图进行压缩,池化层就是将压缩得到的feature map经过池化得到更小的feature map
作用:对特征图进行压缩(使特征图变小),简化计算量;进行特征压缩,提取主要特征(关注重要特征);增大感受野。
-最大池化:

通过对输入的特征图来进行压缩,压缩之后得到更小的特征图,采用2x2的最大池化和步长为2的压缩。
filter:2x2:每次取2x2的窗口,采用Max pool处理,即从2x2的区域中取出最大值,第一个窗口池化为6,步长为2,第二个窗口最大值为8,同理,可得到最终结果。
池化后得到2x2的特征图,该特征图对应原先图中2x2的区域,相比原始图像,压缩后的图每一个部分对应了更大的感受野。
最大池化等池化过程都是提取部分区域的主要特征,从4x4到2x2,在池化层和卷积层都可以进行下采样,而卷积层下采样增加步长会损失精度,所以考虑是在池化层下采样还是卷积层下采样,需要综合考虑,使其平衡。
常见池化策略
- 最大池化(Max Pooling)
- 平均池化(Average Pooling)
- 随机池化(Stochastic Pooling)
注意:池化层无参,即在进行反向传播BP时,池化层不会进行参数优化,可以将池化层理解成一种运算,这种运算就是对当前图像进行下采样。
激活函数(激活层)
激活函数:为了增加卷积神经网络的非线性,进而提升网络的表达能力,对于一个卷积神经网,如果全部的网络结构都由卷积构成,卷积是线性运算,如果将多个卷积网堆叠,即将多个线性运算堆叠,堆叠之后整个网络依然是线性的。在解决实际任务时,很多实际任务是非线性的,通过线性网络解决非线性的问题,就很难有效解决这个任务,就需要对网络增加非线性的表达能力。采用Pooling层,可以理解对网络层增加了非线性的元素,激活函数就是进一步增加网络的非线性表达能力。
常见的激活函数: Sigmoid,Tanh,ReLU,ELU,Maxout,Softplus,Softsign
激活函数特点: 非线性、单调性、可微性、取值范围
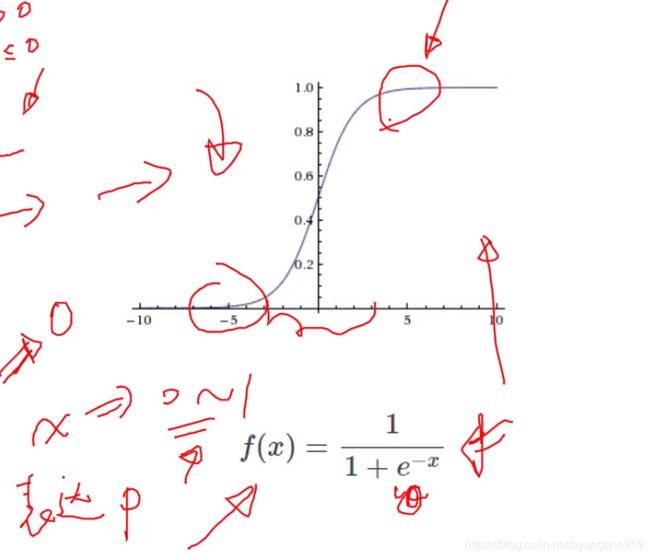
Sigmoid
- 将值的范围约束在0~1之间,0~1可以表达概率(进行分类任务),拿到预测结果的概率分布
- 值在两端时接近0和1,0~1的中间区域相对变化较快
缺点: - 容易出现梯度弥散/梯度饱和:x值趋近于∞时,sigmoid导数均为0,或者是接近0的数,梯度值很小,在网络中间插入多个sigmoid层,这些接近于0的导数经过链式法则连乘后发生梯度弥散,导数为0
- 存在指数运算
- 输出结果不是以0为中心,而是0.5(影响寻找最优解的收敛次数)
一般将sigmoid作为最后的输出层,将输出值约束到0~1之间,很少用在中间层,循环神经网中使用较多
Tanh
- 双曲正切函数
- 对称中心在原点,完全可微分,反对称
- 指数运算
- 取值-1~1
- 一般用于循环神经网,基本不在卷积神经网中使用
ReLU
- 修正线性单元
- ReLU函数将小于0的数置为0,保留了step函数的生物学启发(只有超出阈值时神经元才激活),只有当x值大于0时才会有值,否则为0
- 函数形式简单,正数时不存在梯度饱和
- 一旦输入到了负数,ReLU就会死掉
BathchNorm层
通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布。
规范化操作:
如果不将输入的数据进行规范化处理,那么输入的数据是不可控的,每一层的数据分布都是有差异的,每一轮的BP算法都会改变相应层的参数,参数改变,则输出也会改变,则训练时每一层和不同层之间数据分布一直变化,对网络的收敛很不利,所以利用BN层对数据进行规范化处理。
BatchNorm层优点:
- 减少了参数的人为选择,可以取消Dropout和L2正则项参数,或者采取更小的L2正则项约束参数(均值0,方差1)
- 减少了对学习率的要求
- 可以不再使用局部相应归一化,BN本身就是归一化网络(局部相应归一化----AlexNet)
- 破坏原来的数据分布,在一定程度上缓解过拟合(数据引入噪声,缓解过拟合)
BatchNorm层的使用
全连接层
连接所有的特征,将输出值送给分类器
(各层之间一一连接,及其关系)
- 将网络的输出变成一个向量
- 可以采用卷积代替全连接层
- 全连接层是尺度敏感的
- 配合使用dropout层
将输入的四维向量(n,h,w,c)通过输入层转化成向量,输入层的全部节点同输出层的节点一一相连,使得全连接层数据量很大,每个连接都是线性运算(Y=wx+b)
全连接层对输入数据敏感,每个连接线对应一个参数,如果输入数据大小发生变化,连线的数量也会发生变化,全连接层参数的数量也会发生变化,所以存在全连接层时,不能改变数据输入的尺寸大小,因为全连接层参数固定,如果大小变化就要去掉全连接层。
Dropout

在训练过程中,随机的丢弃一部分输入,此时丢弃部分对应的参数不会更新
丢弃的部分数据对应参数置为0
参数为0的个数尽可能多,则越简单
同一层,训练时会丢弃一些输入,每次随机的结果都不一样,就会使同一层进行前向推理时每次训练都是不同的网络结构,不同的网络结构需要得到最终相同的输出结果,因此引入dropout层,可看作引入多个网络平均的结果,每次随机丢失一些元素,保证了最终的输出结果不会依赖于某些特定的元素,对于中间隐藏层的节点,层和层之间也会减少神经元之间复杂的共适应关系
解决过拟合问题:
- 取平均的作用
- 减少神经元之间复杂的共适应关系
损失层
损失函数:
损失函数:用来评估模型的预测值和真实值的不一致程度
神经网络,模型即网络,网络结构的搭建和参数的取值,前向预算得到预测值,真实值为结果的标签,预测值和真实值的差异即BP算法
-
经验风险最小:交叉熵损失、softmax loss等
-
结构风险最小(模型的复杂程度越低,结构风险越小,模型越简单,越不容易过拟合):L0范式(0值最多,越简单,无法求导,实现稀疏的特性),L1范式(参数绝对值,不能求导,实现参数稀疏的特性,减小过拟合风险),L2范式(参数平方和,可以求导)等
过拟合:过度拟合
损失层
损失层定义了使用的损失函数,通过最小化损失来驱动网络的训练(找到一组参数使损失最小)
损失层一般定义了经验风险最小,结构风险最小需要单独定义
- 网络损失通过前向操作计算
- 网络参数相对于损失函数的梯度则通过反向操作计算
- 分类任务(离散)损失:交叉熵损失
- 回归任务(连续)损失:L1损失、L2损失
交叉熵损失:
似然–>在已知结果的情况下反推产生结果的原因,原因即要学习的参数,找到一组参数,通过参数得到已知的结果
交叉熵损失可以看作似然损失
非负性:最小值接近0
当真实输出a与期望输出y接近的时候,代价函数接近于0
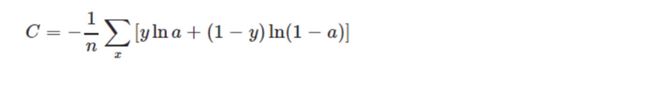
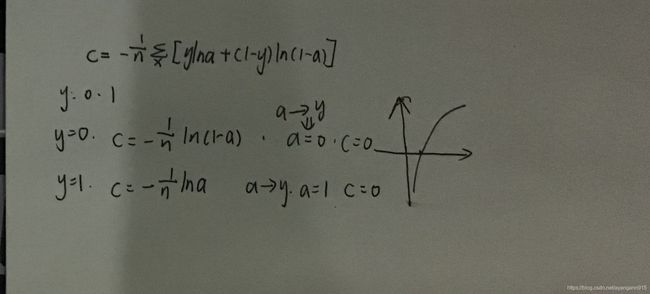
二分类任务:a 和 1-a,两种不同任务的概率
y:实际标签:0分类,1分类
熵:p*lnp,p为概率,熵是对信息量化的概念,定义了当前事件的不确定性,不确定性越大,熵越大,所需要的信息量越大。
优化时尽可能希望代价越小越好,即c越小
当c越大时,熵越大,a=0.5,当前模型越不靠谱,很难分清当前模型属于0还是1, [0.5,0.5]
交叉熵损失实现
回归任务L1,L2,Smooth L1损失
Smooth L1是L1的变形,用于Faster RCNN、SSD等网络计算损失

L1损失:定义了当前输出结果同真实值之间的偏差,用绝对值表示,最终的偏差为绝对值之和
L2损失:定义当前输出结果同真实值之间差的平方
smooth L1:综合考虑L1和L2的优缺点
卷积神经网的介绍
LeNet
- 解决手写数字识别,MNIST
AlexNet
- con—relu—pooling—LRN
con:卷积
relu:激活,增加非线性表达能力
pooling:下采样,增大感受野,进一步提取特征
LRN:归一化处理,对数据约束,使网络更好的收敛 - fc—relu—dropout
fc:全连接
relu:激活
dropout:约束参数规模 - fc—softmax
fc:特征提取
softmax:映射到1000维向量中,最终在1000个概率中的分布
AlexNet的特点
- ReLU非线性激活函数
- Dropout层防止过拟合
- 数据增强,减少过拟合
- 标准化层(LRN)
ZFNet
ZFNet与特征可视化
过程: 经过pooling层下采样,卷积层特征提取,激活层增加网络的非线性表达能力,下采样层到激活层的过程,对图像造成不可逆的破坏,可视化是要对图像进行更高层次的分析,具体过程是,上采样即unpooling和卷积来完成,即对图像下采样和卷积之后,再反向上采样和卷积,之后得到同原始图像大小特征相同的特征图。
- 特征分层次体系结构
color—>纹理—>shape(层次加深)
颜色纹理这样的特征是低层次特征,降维等处理后得到中层次,最后得到更详细的图 - 深层特征更鲁棒(对噪声不敏感)
- 深层特征更有区分度
- 深层特征收敛更慢
(网络越深,能得到更好的分类效果,效果更鲁棒,但越来越难以训练)
VGGNet
网络深,卷积多,3x3卷积核,同一尺寸channel数量相同
- 更深的网络结构,结构更加规整、简单
- 全部使用3x3的小型卷积核和2x2的最大池化层
- 每次池化后Feature Map宽度降低一半,通道数量增加一倍
- 网络层数更多,结构更深,模型数量更大
(证明了更深的网络,能够提取更好的特征,成为后续很多网络的backbone,规范化了后续网络设计的思路)
GoogleNet/Inception v1
不仅强调网络的深度(层数),也考虑网络的宽度(更多的卷积)
宽度:同一层channel的数量,数量越多则越宽
输入层,feature map大小为28x28,channel数量为192
如果直接输入到3x3的卷积核和5x5的卷积核,计算量会非常大,在大的卷积核上之前加入1x1的卷积核,channel数量降低到96,降到16,将channel数量减少的feature map输入到3x3的卷积核中,这样就能减少模型的参数量和计算量
特点:
- 更深的网络结构(宽度深度)
- 两个LOSS层,降低过拟合风险,保证网络收敛较好
- 考虑网络宽度
- 巧妙利用1x1的卷积核来进行通道降维,减小计算量
从卷积的角度思量,如何减小网络中的计算量
- 大卷积核5x5,7x7,一般使用在输入层,用于原始数据的输入,之后一般使用3x3,1x1
- 采用步长2,可以减少当前层的卷积量
- 巧妙用1x1降维
ResNet
x^n: x<1时,n—>∞时,梯度消失;x>1,n—>∞时,梯度爆炸
Bottleneck:跳连结构(Short-Cut)恒等映射,解决梯度消失问题