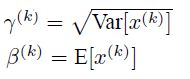深度学习损失函数、优化器选择——调参与优化
早些年很多深度学习的研究人员还在做着调参、炼丹的工作,随着深度卷积神经网络发展到现在,调参的工作渐渐地不被看重,甚至出现了很多自动调参的工具。本文就深度学习中经常使用的损失函数、优化器、学习率迭代策略等进行介绍。
一、损失函数
损失函数是指用于计算标签值和预测值之间差异的函数,对于不同的任务,使用的损失函数也不相同,在目标检测等领域,损失函数往往需要自己定义。
1、L1 Loss
L1Loss 计算的是预测值和真实值之间绝对误差的平均数。公式如下所示:
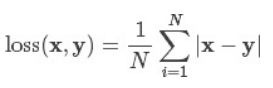
#pytorch代码
torch.nn.L1Loss(size_average=None, reduce=None)
参数:
reduce(bool) 返回值是否为标量,默认为True
size_average(bool) 当reduce=True时有效。为True时,返回的loss为平均值;为False时,返回各样本的loss之和
官方文档中仍有reduction='elementwise_mean’参数,但代码实现中已经删除该参数
2、MSE Loss
MSE Loss 计算的是预测值和真实值之间平方和的平均数。公式如下所示:
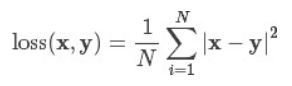
#pytorch代码
torch.nn.MSELoss(size_average=None, reduce=None)
3、Smooth L1 Loss
此方法由微软RGB提出,Smooth L1 Loss方法当预测值和真实值的误差在(-1,1)范围内是平方损失,其余情况下是L1损失,计算公式如下:
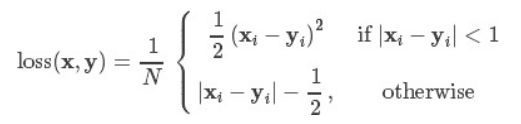
#pytorch代码
torch.nn.SmoothL1Loss(size_average=None, reduce=None)
分析:假设x为预测值和真实值之间的数值差异,上述3个损失函数对x的导数分别为:
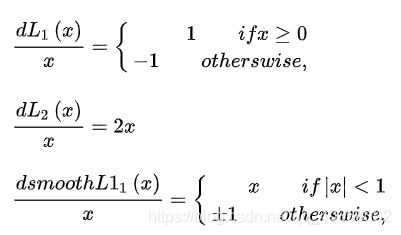
从损失函数对x的导数可知: L1损失函数对x的导数为常数,在训练后期,x很小时,如果learning rate 不变,损失函数会在稳定值附近波动,很难收敛到更高的精度。 MSE损失函数对x的导数在x值很大时,其导数也非常大,在训练初期不稳定。Smooth L1 Loss完美的避开了L1损失和MSE损失的缺点。
4、交叉熵损失
交叉熵损失函数常用语图像分类的神经网络中,计算公式如下:
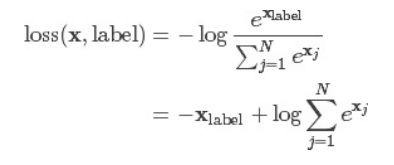
交叉熵损失又称为对数似然损失,在分类任务中,经常采用softmax激活函数+交叉熵损失函数,因为交叉熵描述了两个概率分布的差异,然而神经网络输出的是向量,并不是概率分布的形式,所以需要softmax激活函数将一个向量进行“归一化”成概率分布的形式,再采用交叉熵损失函数计算loss。
在pytorch代码实现时,将nn.LogSoftmax()和 nn.NLLLoss()进行了结合。严格意义上的交叉熵损失函数应该是nn.NLLLoss()。
#pytorch代码
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')
参数:
weight(Tensor)- 为每个类别的loss设置权值,常用于类别不均衡问题。weight必须是float类型的tensor,其长度要于类别C一致,即每一个类别都要设置有weight。
size_average(bool)- 当reduce=True时有效。为True时,返回的loss为平均值;为False时,返回的各样本的loss之和。 reduce(bool)- 返回值是否为标量,默认为True
ignore_index(int)- 忽略某一类别,不计算其loss,其loss会为0,并且,在采用size_average时,不会计算那一类的loss,除的时候的分母也不会统计那一类的样本。
reduction=‘mean’|‘none’|‘sum’| mean表示最后的交叉熵损失会做平均,sum表示求和,none则不做任何操作
5、BCE Loss
BCE Loss是二分类任务时的交叉熵损失函数,可以认为是CrossEntropyLoss的特例。其分类限定为二分类,y必须是{0,1}。还需要注意的是,input应该为概率分布的形式,这样才符合交叉熵的应用。所以在BCELoss之前,input一般为sigmoid激活层的输出,官方给出的公式如下所示:

#pytorch代码
torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')
参数和交叉熵损失相同
6、BCEWithLogitsLoss
将BCELoss和Sigmoid结合,在计算BCELoss之前先经过Sigmoid激活函数,将x变成概率分布的形式之后计算损失。公式如下:

#pytorch代码
torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)
参数和BCE Loss相同,多出来的pos_weight表示正样本的权重,其长度要于类别C一致,即每一个类别都要设置有pos_weight。
7、IOU及其改进版本
在目标检测领域,通常需要对预测的box框和真实框计算交并比,并将其作为判断边界框回归好坏的标准。Bounding Box Regeression的Loss近些年的发展过程是:
IoU Loss(2016)-> GIoU Loss(2019)-> DIoU Loss(2020)->CioU
好的目标框回归损失应该考虑三个重要的几何因素:重叠面积,中心点距离,长宽比。
1、Intersection over Union (IoU) 是目标检测里一种重要的评价值。IoU 通过计算GT_box和Predict_box这两个框 之间的 Intersection Area I 和 Union Area U 的比值来获得:
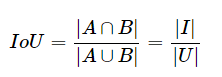
存在的问题:当预测框和目标框不相交时,无法反应两个框距离的远近。当两个预测框大小相同且IOU相同时,无法区分两者相交的情况。
2、GIOU
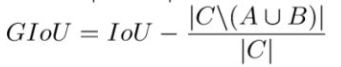
其中C为A和B的外接矩形。用C减去A和B的并集除以C得到一个数值,然后再用框A和B的IoU减去这个数值即可得到GIoU的值。GIOU具有尺度不变性
3、DIOU
当目标框完全包裹预测框的时候,IoU和GIoU的值都一样,此时GIoU退化为IoU, 无法区分其相对位置关系;此时作者提出的DIoU因为加入了中心点归一化距离,所以可以更好地优化此类问题。

如图所示,b和b^gt分别表示预测框和真实框的中心点,ρ表示欧氏距离,c表示预测框和真实框的最小外界矩形的对角线距离。
4、CIOU
CIoU的惩罚项是在DIoU的惩罚项基础上加了一个影响因子αν,这个因子把预测框长宽比拟合目标框的长宽比考虑进去。
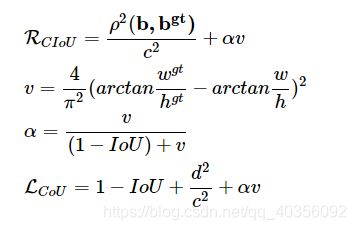
α是用于做trade-off的参数,ν用来衡量长宽比一致性的参数。
二、优化器
pytorch文档中提到的优化器种类有十多种,但是在论文和实际使用中主要以adam优化器为主,偶尔可能会用到SGD优化器。之前也做过一些对比实验,基本上都是adam优化器的效果最好。本文主要介绍Adam和SGD优化器这两种。
在深度学习⾥,⽬标函数通常是训练数据集中有关各个样本的损失函数的平均。设fi(x)是有关索引为i
的训练数据样本的损失函数,n是训练数据样本数,x是模型的参数向量,那么⽬标函数定义为:
![]()
目标函数在x处的梯度为:
![]()
如果使⽤梯度下降,每次⾃变量迭代的计算开销为O(n) ,它随着n线性增⻓。因此,当训练数据样本数很⼤时,梯度下降每次迭代的计算开销很高。
1、SGD
随机梯度下降法(SGD, Stochastic Gradient Descent)减少了每次迭代的计算开销,在随机梯度下降的每次迭代中,随机均匀选取一个样本索引i,并计算梯度▽fi(x)来迭代x:
![]()
梯度下降的计算开销就从O(n)降低到了常数O(1),同时随机梯度▽fi(x)也是对梯度▽f(x)的无篇估计。
#pytorch代码
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
params: 待优化参数
lr 学习率 通常设置为1e-3、1e-4、1e-5等
momentum 动量因子,通常设置为0.8、0.9
weight_decay 权重衰减
dampening 动量的抑制因子
nesterov 是否使用nesterov动量
优点:
虽然SGD需要走很多步的样子,但是对梯度的要求很低(计算梯度快)。而对于引入噪声,大量的理论和实践工作证明,只要噪声不是特别大,SGD都能很好地收敛。
应用大型数据集时,训练速度很快。比如每次从百万数据样本中,取几百个数据点,算一个SGD梯度,更新一下模型参数。相比于标准梯度下降法的遍历全部样本,每输入一个样本更新一次参数,要快得多。
缺点:
SGD在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确。
此外,SGD也没能单独克服局部最优解的问题。
2、Adam优化器
Adam是将Momentum算法和RMSProp算法结合起来使用的一种算法,这些算法网上有非常多的教程,这里仅提供代码和参数的设置。
#pytorch代码
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
参数:

params: 待优化参数
lr 学习率 通常设置为1e-3、1e-4、1e-5等
betas 用于计算梯度以及梯度平方的运行平均值的系数,一般不用
eps 为了增加数值计算的稳定性而加到分母里的项,一般不用
weight_decay 权重衰减
优点:
1、对目标函数没有平稳要求,即loss function可以随着时间变化
2、参数的更新不受梯度的伸缩变换影响
3、更新步长和梯度大小无关,只和alpha、beta_1、beta_2有关系。并且由它们决定步长的理论上限
4、更新的步长能够被限制在大致的范围内(初始学习率)
5、能较好的处理噪音样本,能天然地实现步长退火过程(自动调整学习率)
6、很适合应用于大规模的数据及参数的场景、不稳定目标函数、梯度稀疏或梯度存在很大噪声的问题
三、学习率更新策略
梯度下降算法需要我们指定一个学习率作为权重更新步幅的控制因子,所以学习率更新策略往往配合着优化器使用。一般来说,我们希望在训练初期学习率大一些,使得网络收敛迅速,在训练后期学习率小一些,使得网络更好的收敛到最优解。常用的学习率衰减类型有:指数衰减、固定步长的衰减、多步长衰、余弦退火衰减。
指数衰减:学习率每经过一个epoch乘以一个指数gamma
固定步长衰减:学习率每隔一定epoch就减少为原来的gamma分之一,其中step_size表示步长间隔
余弦退火衰减:学习率按照余弦函数周期性变化,参数T_max表示余弦函数周期;eta_min表示学习率的最小值,默认它是0表示学习率至少为正值,last_epoch表示下降到的最后一个epoch,默认-1
CosineAnnealingWarmRestarts:相比于余弦退火衰减,学习率衰减速度会逐渐变慢,周期数增加。参数T_0表示学习率第一次回到初始值的epoch位置,T_mult表示学习率周期增加因子,其余参数与预先退火衰减相同。
#指数衰减
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
#固定步长衰减
torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.65)
#余弦退火衰减
torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=50, eta_min=0, last_epoch=-1)
#不等间隔的余弦退火衰减
torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1, verbose=False)
下面的图展示了CosineAnnealingLR和CosineAnnealingWarmRestarts两种学习率迭代策略的区别:

四、补充
1、Focal loss
Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重,也可理解为一种困难样本挖掘。
Focal loss是在交叉熵损失函数基础上进行的修改,对于二分类交叉熵损失:
![]()
加上Focal loss之后:
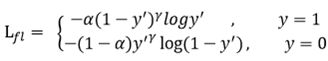
首先在原有的基础上加了一个因子,其中gamma>0能够减少易分类样本的损失,更加关注于困难的、错分的样本。
例如gamma为2,对于正类样本而言,预测结果为0.95肯定是简单样本,所以(1-0.95)的gamma次方就会很小,这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样,预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时,损失只减少了0.25倍,所以更加关注于这种难以区分的样本。这样减少了简单样本的影响,大量预测概率很小的样本叠加起来后的效应才可能比较有效。
此外,加入平衡因子alpha,用来平衡正负样本本身的比例不均:论文中alpha一般取0.25,即正样本要比负样本占比小,这是因为负例易分。
2、Label Smooth 标签平滑
label smooth通常用于分类任务中,相当于一个正则化的作用,目的是防止模型在训练时过于自信地预测标签,改善泛化能力差的问题。但如果网络本身就是欠拟合的,用这个可能意义就不大。
简单说就是,label smooth将类别分组,每组之间会有一个margin(类别之内更紧密,类别之间距离更大,也就是分得更开。
代码实现如下:
def smooth_labels(y_true, label_smoothing, num_classes):
return y_true * (1.0 - label_smoothing) + label_smoothing / num_classes
此方法运用并不多,一方面原因是防止过拟合的方法很多,而且对于数据量极大的网络来说,很多时候都处于欠拟合的状态,对结果的影响并不都是正面的;标签平滑后的分布就相当于往真实分布中加入了噪声,能够有效提高模型的鲁棒性,对于准确率的提升微乎其微,现阶段的研究中人们关注的往往都是模型的准确率,在鲁棒性方面的研究并不多。
3、Batch Normalization 批量归一化
BN层在网络中主要的作用是对输入数据进行归一化,解决卷积神经网络在训练过程中,中间层数据分布发生改变的情况。它是一个可学习、有参数(γ、β)的网络层,其前向传播公式为:
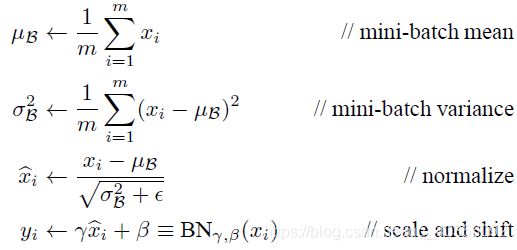
m = K.mean(X, axis=-1, keepdims=True) #计算均值
std = K.std(X, axis=-1, keepdims=True) #计算标准差
X_normed = (X - m) / (std + self.epsilon) #归一化
out = self.gamma * X_normed + self.beta #重构变换
参考网址:
[1] Pytorch的损失函数
[2] Pytorch优化器总结
[3] pytorch必须掌握的的4种学习率衰减策略
[4] BN使用总结及启发