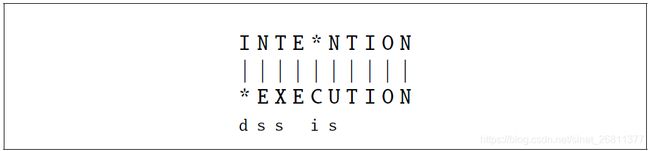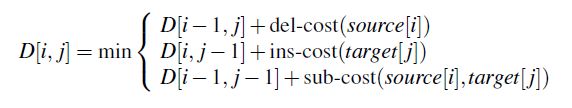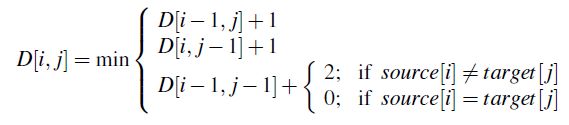编辑距离(Edit Distance) 一文读懂（Python实现）

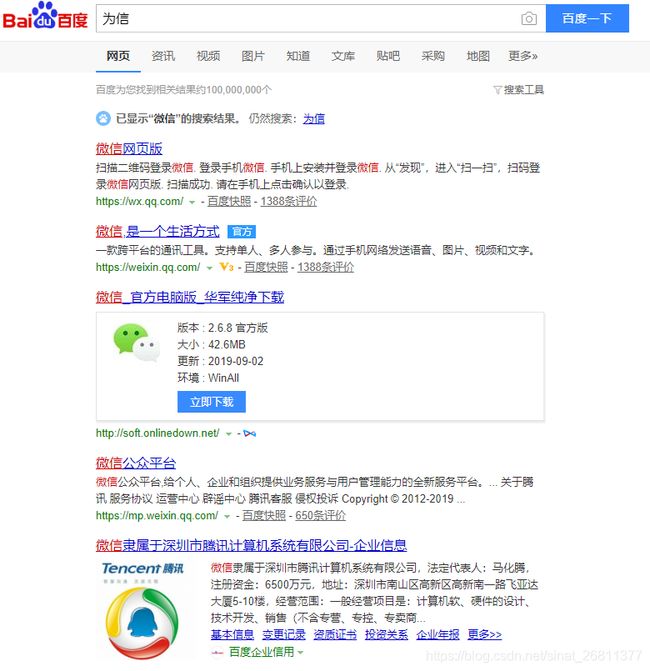
在NLP任务中经常会碰到比较两个字符串的相似度，比如拼写纠错和指代判断。用户很可能在搜索时输入错别字，比如“微信”输成了“为信”，但是搜索引擎返回的结果纠正为“微信”的搜索结果，如图1-1。另外比如“北京大学校长”和“北大校长”，“北京故宫博物院”和“北京故宫”都是指的同一个人或事物。

上述问题，可以利用两个词或短语的编辑距离大小来解决。

图1-1 搜索词“为信”的百度结果

 

编辑距离介绍

利用编辑距离可以判断两个字符串的相似程度，即从一个字符串到另一个字符串所需要的编辑次数，包括插入字符，删除字符及替换字符这三种操作。最小编辑距离即从一个字符串到另一个字符串所需要的最小编辑次数。

在这里定义的单字符编辑操作有且仅有三种：

• 插入（Insertion）
• 删除（Deletion）
• 替换（Substitution）

图2-1所示将两个字符串进行排列比对，上面的字符串INTENTION进行一系列操作可以变为下面的字符串EXECUTION,  d代表删除字符操作，s代表替换字符操作，i代表插入字符操作。

图2-1 编辑距离计算

 

可以给不同的操作赋予不同代价值，莱温斯坦（Levenshtein）定义该编辑距离最简单的方式是给每种操作赋予相同的代价值1，这样上述两个字符串的编辑距离为5。莱温斯坦另外一种定义只允许插入和删除操作，不允许替换操作。这样相当于替换用插入和删除两种操作实现，替换的代价值相当于变成2，上述两个字符串的编辑距离为8。

 

最小编辑距离算法

那么如何找到最小编辑距离呢？可以看作是一种操作路径的搜索，从一个字符串转变为另一个字符串的最短搜索路径。图3-1描述了intention字符串经过三种不同的操作路径，转变为三个不同的字符串。

  图3-1 将编辑距离看成搜索问题

 

从一个字符串转到另一个字符串的可能路径是非常多的，所有不同的操作路径，最终都会到达一种状态。采用动态规划的方法，每一种状态都记录下来最短的路径，然后从最终状态进行回溯。动态规划把一个大的问题转换成很多的子问题来处理，intention和execution的最短编辑距离的操作步骤如图3-2所示。

图3-2 intention到execution的最小操作

 

最小编辑距离同时被多个人独立发现，由Wagner和Fischer在1974年命名。让我们先定义两个字符串间的最小编辑距离。有两个字符串X和Y，X长度为n，Y长度为m。D[i, j] 为X[1..i]到Y[1.. j]的最小编辑距离。X[1..i]表示X的前i个字符，Y[1.. j]表示Y的前j个字符，D[n,m]为X和Y的最小编辑距离。

采用动态规划方法计算D[n,m], D[i,j]从小到大采用图3-3计算，del-cost表示删除操作的代价值，ins-cost表示插入操作的代价值，sub-cost表示替换操作的代价值，source表示原字符串，target表示转换的目标字符串。如果定义插入和删除的代价值为1，替换的代价值为2，计算方法如图3-4所示。

图3-3 最小编辑距离计算

       

图3-4 明确代价值的最小编辑距离计算

 

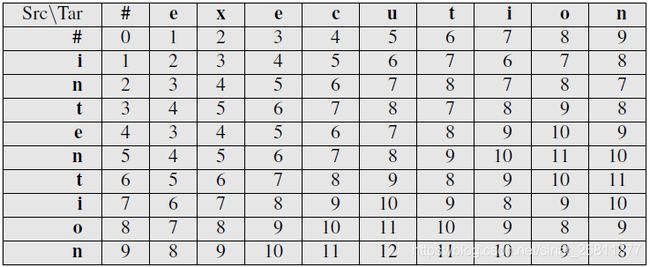
最小编辑距离算法总结如图3-5，图3-6列出了intention和execution字符串跟根据图3-5计算方法，算法的详细计算结果。

 

图3-6 intention和execution字符串最小编辑距离计算示例

 

编辑距离除了被大家所熟知的应用如拼写纠错，编辑距离在另外的方面还有重要作用，如两个字符串比对的最小代价计算。字符串比对在语音识别和语言处理领域有着广泛的应用，在语音识别领域最小编辑距离比对通常用来计算错词率。比对在机器翻译领域也扮演了重要的角色，在一个句子中每个词在两种语言中会有不同的词来表示，它们需要相互比对。

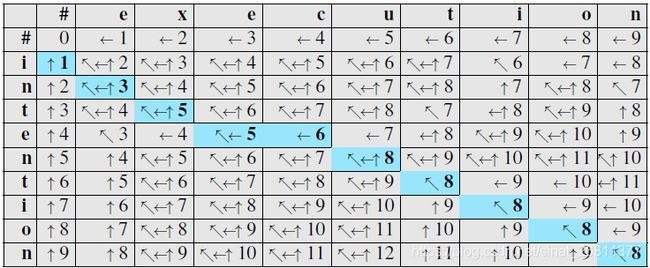
为了使编辑距离算法能够处理字符串比对，我们通过编辑距离矩阵标出一个比对路径，图3-7采用粗体蓝色单元格表示出这样一条路径。每个单元格代表两个字符串中的一对字符的比对结果，如果粗体单元格出现在同一行的相邻位置，那么从原字符串到目标字符串发生了一次插入操作；粗体单元格出现在同一列的相邻位置，那么从原字符串到目标字符串发生了一次删除操作。

图3-7 一种计算比对路径的思路

第一步采用最小编辑距离算法对每个单元格计算并存储一个回溯指针，即到达这个单元格的前一单元格的位置。图3-7有些单元格有多个回溯指针，代表有多种路径到达该单元格。

第二步开始回溯，从最后一个单元格开始（即最大行和最大列的单元格），跟随回溯指针的方向回溯该矩阵，从最后单元格开始到第一个单元格的每一条完整路径都代表一个最小比对距离。

形式化定义

示例

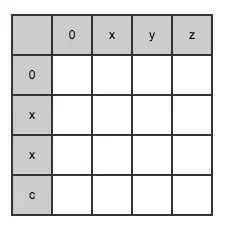
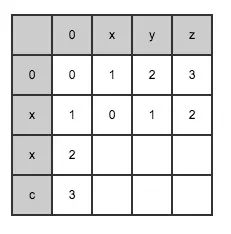
以  xxc 和 xyz 为例，建立一个矩阵，通过矩阵记录计算好的距离：

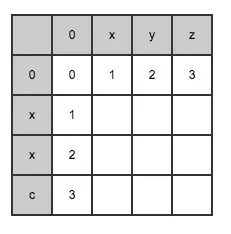
第一行（index = 0）初始化：
min(0, 0) = 0 ->  lev_{a, b}(0, 0) = max(0, 0) = 0
min(0, 1) = 0 ->  lev_{a, b}(0, 1) = max(0, 1) = 1
min(0, 2) = 0 ->  lev_{a, b}(0, 2) = max(0, 2) = 2
min(0, 3) = 0 ->  lev_{a, b}(0, 3) = max(0, 3) = 3

第一列（index = 0）初始化：
min(0, 0) = 0 ->  lev_{a, b}(0, 0) = max(0, 0) = 0
min(1, 0) = 0 ->  lev_{a, b}(1, 0) = max(1, 0) = 1
min(2, 0) = 0 ->  lev_{a, b}(2, 0) = max(2, 0) = 2
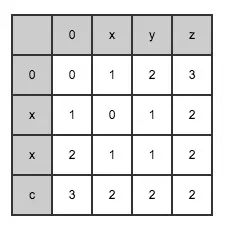
min(3, 0) = 0 ->  lev_{a, b}(3, 0) = max(3, 0) = 3

依据上面的公式可以继续推导出第二行：

 

Python实现

1. 递归方式

def Levenshtein_Distance_Recursive(str1, str2):

    if len(str1) == 0:
        return len(str2)
    elif len(str2) == 0:
        return len(str1)
    elif str1 == str2:
        return 0

    if str1[len(str1)-1] == str2[len(str2)-1]:
        d = 0
    else:
        d = 1
    
    return min(Levenshtein_Distance_Recursive(str1, str2[:-1]) + 1,
                Levenshtein_Distance_Recursive(str1[:-1], str2) + 1,
                Levenshtein_Distance_Recursive(str1[:-1], str2[:-1]) + d)

print(Levenshtein_Distance_Recursive("abc", "bd"))

2. 动态规划
递归是从后向前分解，那与之相对的就是从前向后计算，逐渐推导出最终结果，此法被称之为动态规划。动态规划很适用于具有重叠计算性质的问题，但这个过程中会存储大量的中间计算的结果，一个好的动态规划算法会尽量减少空间复杂度。

def Levenshtein_Distance(str1, str2):
    """
    计算字符串 str1 和 str2 的编辑距离
    :param str1
    :param str2
    :return:
    """
    matrix = [[ i + j for j in range(len(str2) + 1)] for i in range(len(str1) + 1)]

    for i in range(1, len(str1)+1):
        for j in range(1, len(str2)+1):
            if(str1[i-1] == str2[j-1]):
                d = 0
            else:
                d = 1
            
            matrix[i][j] = min(matrix[i-1][j]+1, matrix[i][j-1]+1, matrix[i-1][j-1]+d)

    return matrix[len(str1)][len(str2)]


print(Levenshtein_Distance("abc", "bd"))

 

小结

本文是对编辑距离及最小编辑距离算法及其应用的简单介绍，主要内容参考《Speech and Language Processing (3rd ed. draft)》第二章部分章节进行翻译，大部分图片均来源于该书，疏漏和错误之处，望批评指正。