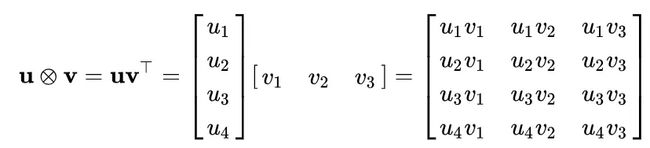【学习】RNN、积
一、积
向量和矩阵中有内积、外积等运算，但由于Outer Product和Exterior Product中文翻译都是“外积”。
Outer Product是线性代数中的外积(WikiPedia: Outer Product)，也就是张量积 ；
Exterior Product是解析几何中的外积(WikiPedia: Exterior Algebra)，又叫叉乘(WikiPedia: Cross Product)，即两个向量的法向量，一般用在三维空间。
1、向量内积（Inner product） ：
A·B，
这个最好理解，又叫向量点乘,也叫向量的内积、数量积。顾名思义,求下来的结果是一个数.
向量a·向量b=|a||b|cos
在物理学中,已知力与位移求功,实际上就是求向量F与向量s的内积，即要用点乘。
2、Outer Product
又称张量积，例如线性代数中一列乘一行得到的一个矩阵，两个向量的Outer Product是一个矩阵
一般写作 aⓧb
注意：np中多维向量的外积都是先拉平，再求外积，如下（和矩阵外积有区别）：
3、Exterior Product
（即中学课本常见的“外积”）：
又称作叉乘，如下图所示，写作 a X b，几何意义为两个向量的法向量
4、矩阵外积（升维运算）
5、 矩阵内积：
一般认为，矩阵内积是矩阵对应元素成绩之和，类似于CNN的卷积。
6、矩阵元素积（element-wise product, point-wise product, Hadamard product）
一般指Hadamard product（哈达玛积），如下所示：一般写作：A⊙B
elementwise multiplication 直白翻译过来就是元素的智能乘积。例如 v⊙w=s表示对每一个输入向量 v乘以一个给定的“权重” w向量。换句话说，就是通过一个乘子对数据集的每一列进行缩放。这个转换可以表示为如下的形式：
7、矩阵点积dot product
点积(dot product)，也称内积(inner product)，标量积（scalar product）
符号：A.B，
1.向量点积。变成一个数。
2.矩阵点积。是每行每列的点积的矩阵
二、RNN
1.1 引例导入
引例：利用前馈神经网络(FFN)解决在空缺位置填充单词问题
FFN:Input:一个单词（一个向量表示一个单词）
Output:输入单词属于空缺位置的概率分布
FNN缺点：神经网络没有记忆力,不考虑上下文,对于不同性质的空缺位置,输入单词的概率分布是相同的。
比如：第一句中Taipei是目的地,而在第二句中是出发地,那么在这两个空缺的地方,Taipei出现的概率不一定是相同的,而利用FNN计算之后Taipei的概率分布始终是不变的,不符合语义.
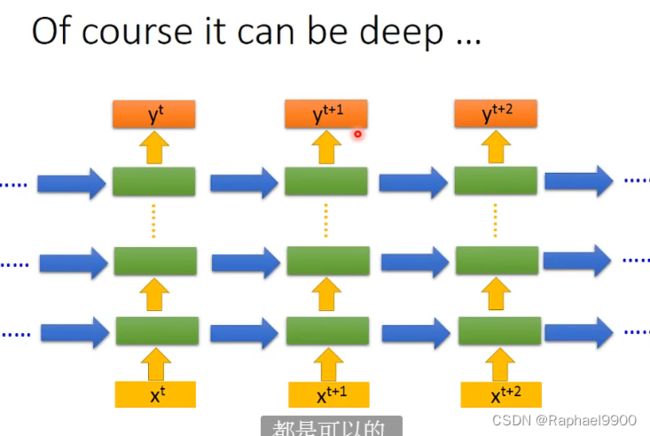
1.2 RNN
RNN：拥有记忆力,考虑上下文内容,相同输入不同概率分布输出的神经网络;
隐藏层的输出存储在内存中,网络的输入不光考虑原始的输入也要考虑隐藏层的输出;
换句话说就是将隐藏层的输出同时作为输入,影响输出.
1.3 举例
输入序列：
条件：所有权重w均为1;没有偏差bias;所有激活函数均为线性函数.
每次的计算都能存到蓝色框里面，然后在下次的计算里面考虑进去（这里是进行简单的相加）。
如果改变输入序列的顺序就会改变输出结果,说明RNN会考虑输入数据的顺序问题，在预测当前结果时，也包括了之前的信息。
可以将RNN结构设计为深度网络
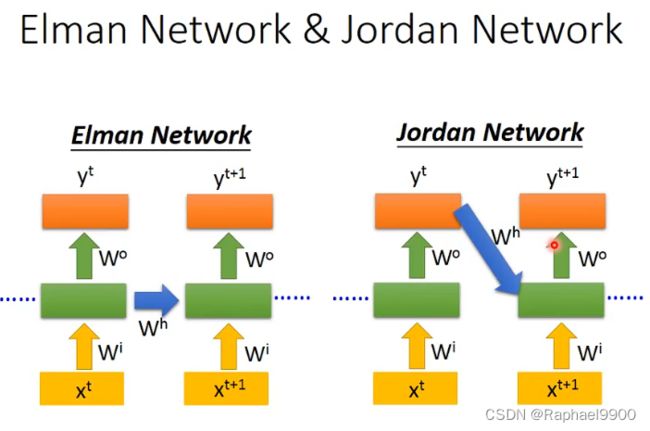
RNN分类：
Elman Network ：将隐藏单元的输出作为下一次预测的输入
Jordan Network：将上一次的预测输出作为下一次预测的输入
由于中间隐藏层输出结果相对来是不可控，最后的输出结果更有意义，相对来说我们知道memory存的是什么信息，所以 Jordan Network比Elman Network性能更好.
双向RNN（Bidirectional RNN):
2 Long Short-term Memeory （LSTM）
比较长的短期记忆
3个门 4输入 1输出
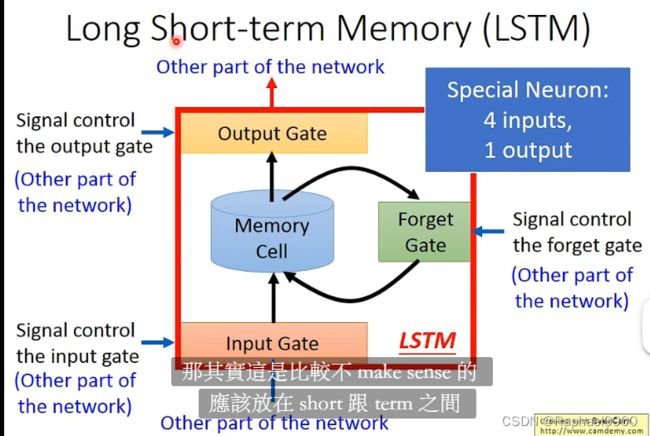
2.1 LSTM 基本组成
LSTM：一个单元中，有4个输入和1个输出，4个输出=3个控制信号和1个输入
组成成分：
Input Gate：控制input数据输入
Forget Gate：控制是否保存中间结果
Output Gate：控制output数据输出
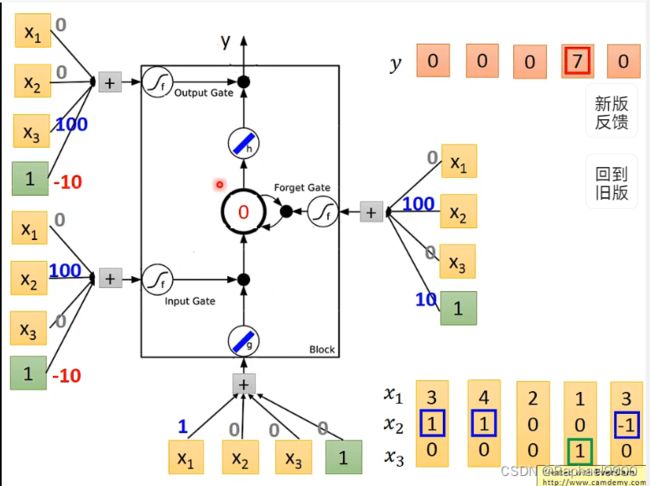
2.2 LSTM实例
输入：2维
输出：1维
控制门信号：
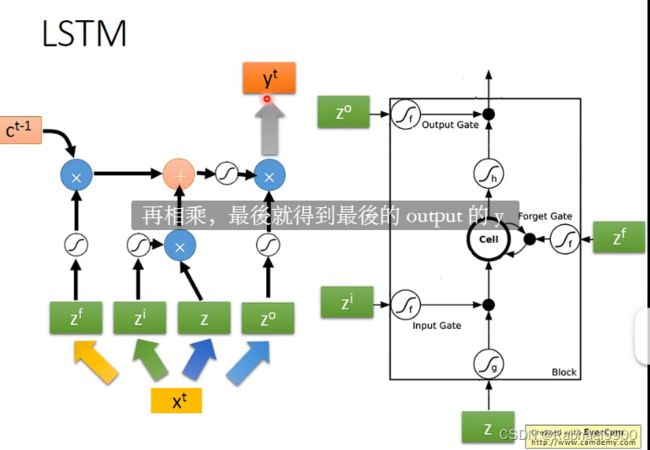
2.3LSTM 结构
原始神经网络和LSTM网络联系
原始神经网络结构如图：
LSTM结构：用LSTM代替神经网络的神经元;
输入乘以4组参数，作为输入进行计算.
设计多层LSTM