利用Tensorflow2构建CNN并用于图像分类
利用Tensorflow2构建CNN并用于图像分类
本文将使用自下而上的方法,从讨论CNN的基本板块构建开始。然后将深入研究CNN的体系结构,并探索如何在TensorFlow中实现CNN。本文包含以下内容:
-
一维和二维的卷积运算
-
卷积神经网络结构的构建
-
使用Tensorflow构建深度卷积神经网络
-
利用数据扩充技术提高模型泛化性能
-
实现一个基于人脸图像的CNN分类器来预测个人性别
from IPython.display import Image
%matplotlib inline
1.CNN网络的模块构建
CNN是一组模型,设计灵感源自人脑的视觉皮层在识别物体时候的工作方式。其最初的发展可以追溯到20世纪90年代,参考文献。
CNN在图像分类领域具有出色性能并得到了广泛关注,领域学者本吉奥、辛顿与杨立坤等人也于2019年获得了图灵奖。
David H. Hubel和Torsten Wiesel在1959年首次发现了大脑的视觉皮层是如何运作的,当时他们在一只被麻醉的猫的初级视觉皮层中植入了一个微电极。然后, 他们观察到,在猫面前投射不同的光模式后,大脑神经元的反应不同。这最终导致了视觉皮层不同层次的发现。主层主要检测边缘和直线,而高阶层更注重提取 复杂的形状和模式。
1.1理解CNN和特征层次(feature hierarchies)
CNN中的卷积架构通常被描述为“特征提取层”。
成功提取显著性(相关)特征是任何机器学习算法性能的关键,传统的机器学习模型依赖于输入特征,这些输入特征可能来自领域专家或基于计算特征提取技术。
CNN能够从原始数据中自动学习到对特定任务最有用的特征。因此,通常将CNN网络layers视为特征提取器。早期层(紧接着输入层之后的层)用于从原始数据
中提取低级特征,而后期层(通常是像多层感知机MLP中的全连接层)则使用这些特恒来预测连续的目标值或者类别标签。
对于某些类型的多层NNs,特别是深度卷积神经网络,通过以分层的方式组合低级特征以形成高级特征来构建所谓的特征层次(feature hierarchy)。
例如:在处理图像的时候,从较早的层中提取低级特征,例如边缘和斑点。这些特征组合在一起形成高级特征。这些高级特征可以形成更加复杂的形状,例如建
筑物、猫和狗等对象的一般轮廓。
如下图所示,CNN根据输入图像计算特征映射(feature maps),其中每个元素都来自输入图像中的局部像素块:
Image(filename='images/15_01.png', width=700)
1.2局部感受野
对上图右面子图:像素的局部补丁或者局部板块被称为局部感受野(Local receptive field)。
CNN在图像相关的任务重具有良好的性能一般归因于两个方面:即局部连接,参数共享
- **稀疏连接**:对于上述特征映射图中的单个元素仅仅连接到一小块像素。这与全连接网络不同,全连接网络则实现连接到整个图像。
- **参数共享**:对于输入图像的不同像素块使用了相同的权重(weights)。
这样做的直接好处:
使用卷积层替代了传统的、完全连接的MLP大大减少了网络中的权重(参数)的数量,且随之带来的是:网络捕获显著特征的能力的提升;
在图像数据的上下文中,对于临近的像素点通常比相隔较远的像素点更具有相关性的假设更有意义;
通常CNN由几个卷积层和子采样层组成,其后是末端的一个或者多个全连接层。完全连接层本质上是一个MLP,其中对于每个输入单元 i i i,通过权重 w i j w_{ij} wij连接到
输出单元 j j j。
注意:子采样层通常被称为池化层,其不具有任何的学习参数。例如,池化层中没有权重或偏置单元。
但是,卷积层和全连接层都具有权重和偏置单元,且均在训练期间进行优化更新。
2.离散卷积(discrete convolutions)
离散卷积(discrete convolutions)或者称为简单卷积,是CNN的基本运算。这里将介绍其数学定义,以及一些计算一维张量(向量)和二维张量(矩阵)卷积的朴素算法。
符号约定:这里使用 A n 1 × n 2 A_{n_{1} \times n_{2}} An1×n2表示多维数组(张量),其size为 n 1 × n 2 n_1\times n_2 n1×n2。使用中括号 A [ i , j ] A[i, j] A[i,j]表示矩阵中的元素。
使用 ∗ * ∗表示两个向量或者矩阵之间的卷积操作。
2.1一维简单卷积
对于向量 x and w \boldsymbol{x} \text { and } \boldsymbol{w} x and w,使用 y = x ∗ w y=x * w y=x∗w进行标记。其中, x \boldsymbol {x} x为输入,也称为信号。
w \boldsymbol{w} w也称为滤波器或者卷积核。计算过程如下:
y = x ∗ w → y [ i ] = ∑ k = − ∞ + ∞ x [ i − k ] w [ k ] \boldsymbol{y}=\boldsymbol{x} * \boldsymbol{w} \rightarrow y[i]=\sum_{k=-\infty}^{+\infty} x[i-k] w[k] y=x∗w→y[i]=k=−∞∑+∞x[i−k]w[k]
上述过程也被称为零填充或者简单填充。几何表示如下:
Image(filename='images/15_02.png', width=700)
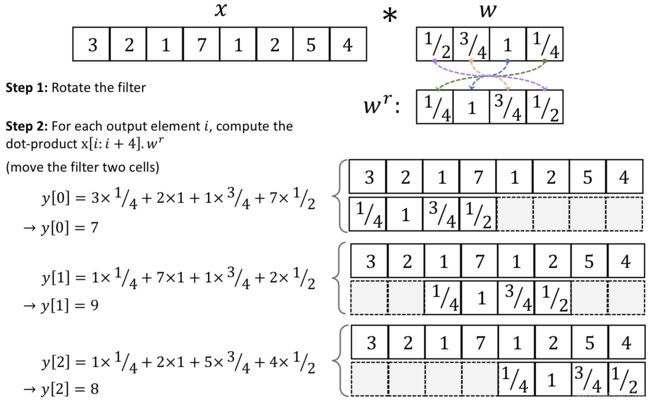
假设原始输入 x \boldsymbol{x} x和滤波器 w \boldsymbol{w} w分别有 n , m n,m n,m个元素,其中 m ≤ n m \le n m≤n。计算如下:
y = x ∗ w → y [ i ] = ∑ k = 0 k = m − 1 x p [ i + m − k ] w [ k ] \boldsymbol{y}=\boldsymbol{x} * \boldsymbol{w} \rightarrow \quad y[i]=\sum_{k=0}^{k=m-1} \boldsymbol{x}^{p}[i+m-k] w[k] y=x∗w→y[i]=k=0∑k=m−1xp[i+m−k]w[k]
计算过程几何表示如下:
Image(filename='images/15_03.png', width=700)
互相关(Cross-correlation):
互相关与卷积的区别可以简单理解为:是否需要翻转卷积核,即图像是否需要进行翻转。互相关也称为不翻转卷积。
除非特殊声明,卷积一般指的是“互相关”,即不翻转卷积,并使用下列符号表示:
Y = W ⊗ X \boldsymbol{Y}=\boldsymbol{W} \otimes \boldsymbol{X} Y=W⊗X
卷积核是否进行翻转与其特征抽取的能力无关,卷积核互相关在能力上式等价的。一般为了描述方便,亦将互相关称为卷积。
更多内容参见:邱锡鹏.神经网络与深度学习[M].北京:机械工业出版社,2020
2.2对输入进行填充以控制特征映射的大小
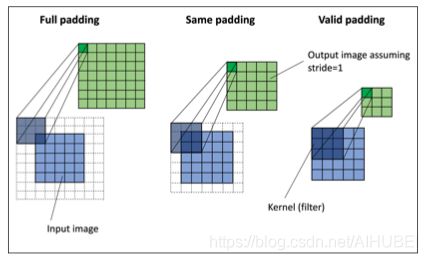
一般常用的卷积或者填充策略有三种:
窄卷积、宽卷积、等宽卷积等;更多内容参见:邱锡鹏.神经网络与深度学习[M].北京:机械工业出版社,2020
# 展示了不同的padding填充模式,卷积核大小为3x3,步长为1,输入为5x5像素
Image(filename='images/524-old.png', width=700)
-
full mode: 填充参数 p p p的设置满足 p = m − 1 p=m-1 p=m−1。full padding 增加了输出的维度,因此在CNN中使用的较少;
-
same mode: 同常被用来确保输出向量与输入向量x具有相同的大小。填充参数 p p p的计算是根据滤波器大小以及输入输出大小相同的要求计算的;
-
valid mode: 在有效模式下计算卷积特指 p = 0 p=0 p=0的情况。
CNN中最常用的是same padding。这种策略的一个优势是,保留了向量的大小,或者在当我们在计算机视觉中处理与图像相关的任务的时候,输入图像的高度和宽
度保持不变。这使得网络架构更加方便;
valid mode 相对于full 和 same 的一个缺点是:在多层神经网络中,张量的体量将大幅减小,这可能会对网络性能造成不利影响;
实践中,建议在卷积层使用same padding来保留空间大小,而改为通过使用池化层来减小空间大小。full mode通常用于信号处理中,将边界效应降低
2.3确定卷积输出的大小
卷积的输出大小由移动滤波器的总次数决定,假设输入向量大小为 n n n,滤波器大小为 m m m,填充参数为 p p p,步长为 s s s,则经过卷积之后:
o = [ n + 2 p − m s ⌋ + 1 o=\left[\frac{n+2 p-m}{s}\right\rfloor+1 o=[sn+2p−m⌋+1
结果向下取整。
import tensorflow as tf
import numpy as np
print('TensorFlow version:', tf.__version__)
print('NumPy version: ', np.__version__)
TensorFlow version: 2.1.0
NumPy version: 1.18.2
def conv1d(x, w, p=0, s=1):
w_rot = np.array(w[::-1])
x_padded = np.array(x)
if p > 0:
zero_pad = np.zeros(shape=p)
x_padded = np.concatenate(
[zero_pad, x_padded, zero_pad])
res = []
for i in range(0, int((len(x_padded) - len(w_rot)) / s) + 1, s):
res.append(np.sum(
x_padded[i:i+w_rot.shape[0]] * w_rot))
return np.array(res)
## Testing:
x = [1, 3, 2, 4, 5, 6, 1, 3]
w = [1, 0, 3, 1, 2]
print('Conv1d Implementation:',
conv1d(x, w, p=2, s=1))
print('Numpy Results:',
np.convolve(x, w, mode='same'))
Conv1d Implementation: [ 5. 14. 16. 26. 24. 34. 19. 22.]
Numpy Results: [ 5 14 16 26 24 34 19 22]
2.4二维离散卷积
对输入矩阵 X n 1 × n 2 \boldsymbol{X}_{n_1\times n_2} Xn1×n2,卷积核为 W m 1 × m 2 \boldsymbol{W}_{m_1\times m_2} Wm1×m2。
其中, m 1 ≤ n 1 m_1\le n_1 m1≤n1, m 2 ≤ n 2 m_2\le n_2 m2≤n2。则卷积操作如下:
Y = X ∗ W → Y [ i , j ] = ∑ k 1 = − ∞ + ∞ ∑ k 2 = − ∞ + ∞ X [ i − k 1 , j − k 2 ] W [ k 1 , k 2 ] \boldsymbol{Y}=\boldsymbol{X} * \boldsymbol{W} \rightarrow \quad Y[i, j]=\sum_{k_{1}=-\infty}^{+\infty} \sum_{k_{2}=-\infty}^{+\infty} X\left[i-k_{1}, j-k_{2}\right] W\left[k_{1}, k_{2}\right] Y=X∗W→Y[i,j]=k1=−∞∑+∞k2=−∞∑+∞X[i−k1,j−k2]W[k1,k2]
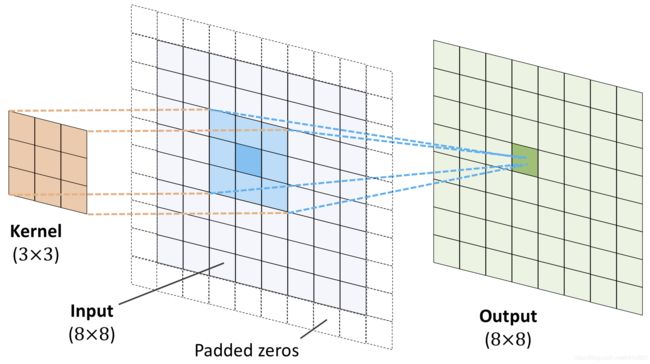
下图中,输入矩阵为8x8, 卷积核为3x3, 使用零填充,填充参数 p p p为1,结果如下:
Image(filename='images/15_05.png', width=700)
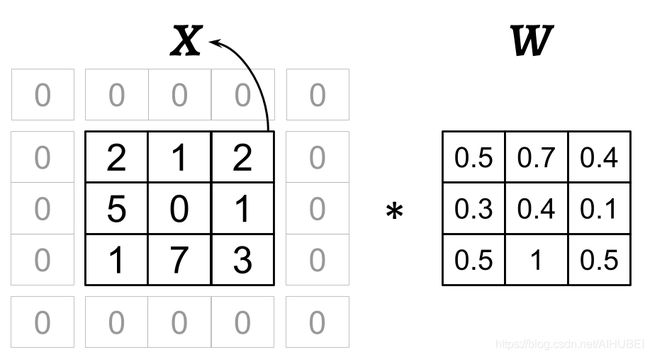
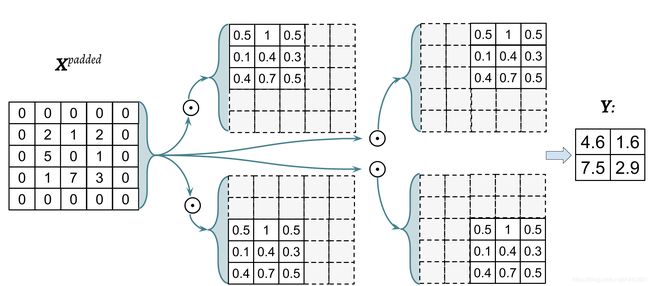
下图显示了输入矩阵为3x3, 卷积核为3x3, 填充参数为1, 步长为2的卷积运算过程:
Image(filename='images/15_06.png', width=600)
旋转之后的卷积核为:
W r = [ 0.5 1 0.5 0.1 0.4 0.3 0.4 0.7 0.5 ] \boldsymbol{W}^{r}= \left[\begin{array}{ccc}0.5 & 1 & 0.5 \\ 0.1 & 0.4 & 0.3 \\ 0.4 & 0.7 & 0.5 \end{array}\right] Wr=⎣⎡0.50.10.410.40.70.50.30.5⎦⎤
上面的翻转操作不等同于矩阵转置。写成Numpy数组切片的形式为:W_rot = W[::-1, ::-1]
翻转之后,执行元素积 ⊙ \odot ⊙,表示如下:
Image(filename='images/15_07.png', width=800)
import scipy.signal
def conv2d(X, W, p=(0, 0), s=(1, 1)):
W_rot = np.array(W)[::-1,::-1] # 卷积核翻转
X_orig = np.array(X)
n1 = X_orig.shape[0] + 2*p[0]
n2 = X_orig.shape[1] + 2*p[1]
X_padded = np.zeros(shape=(n1, n2))
X_padded[p[0]:p[0]+X_orig.shape[0],
p[1]:p[1]+X_orig.shape[1]] = X_orig
res = []
for i in range(0, int((X_padded.shape[0] -
W_rot.shape[0])/s[0])+1, s[0]):
res.append([])
for j in range(0, int((X_padded.shape[1] -
W_rot.shape[1])/s[1])+1, s[1]):
X_sub = X_padded[i:i+W_rot.shape[0],
j:j+W_rot.shape[1]]
res[-1].append(np.sum(X_sub * W_rot))
return(np.array(res))
X = [[1, 3, 2, 4], [5, 6, 1, 3], [1, 2, 0, 2], [3, 4, 3, 2]]
W = [[1, 0, 3], [1, 2, 1], [0, 1, 1]]
print('Conv2d Implementation:\n',
conv2d(X, W, p=(1, 1), s=(1, 1)))
print('SciPy Results:\n',
scipy.signal.convolve2d(X, W, mode='same'))
Conv2d Implementation:
[[11. 25. 32. 13.]
[19. 25. 24. 13.]
[13. 28. 25. 17.]
[11. 17. 14. 9.]]
SciPy Results:
[[11 25 32 13]
[19 25 24 13]
[13 28 25 17]
[11 17 14 9]]
3.子采样层
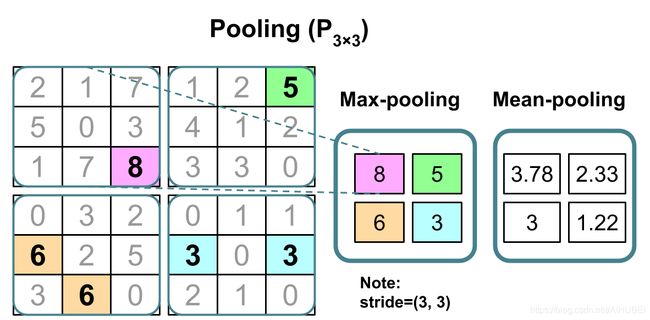
子采样通常用于CNN中的两种池化操作:分别是最大池化和平均池化(max-pooling and mean-pooling)。
池化层通常采用 P n 1 × n 2 P_{n_1\times n_2} Pn1×n2表示。这里的下标决定了执行最大或者平均池化操作的领域的大小(即每个维度中相邻像素的数量)。通常也将
这样的领域称为pooling size。
池化操作的优点:
-
局部不变性:池化(最大池化)操作引入了局部不变性(local invariance)。这意味着局部近邻块的变化不会引起最大池化结果的改变。
因此,它有利于输入数据生成对噪声更加健壮的特征。
示例如下:
X 1 = [ 10 255 125 0 170 100 70 255 105 25 25 70 255 0 150 0 10 10 0 255 10 10 150 20 70 15 200 100 95 0 35 25 100 20 0 60 ] X 2 = [ 100 100 100 50 100 50 95 255 100 125 125 170 80 40 10 10 125 150 255 30 150 20 120 125 30 30 150 100 70 70 70 30 100 200 70 95 ] max pooling P 2 × 2 [ 255 125 170 255 150 150 70 200 95 ] \begin{aligned} &X_{1}=\left[\begin{array}{cccccc} 10 & 255 & 125 & 0 & 170 & 100 \\ 70 & 255 & 105 & 25 & 25 & 70 \\ 255 & 0 & 150 & 0 & 10 & 10 \\ 0 & 255 & 10 & 10 & 150 & 20 \\ 70 & 15 & 200 & 100 & 95 & 0 \\ 35 & 25 & 100 & 20 & 0 & 60 \end{array}\right] \\ &X_{2}=\left[\begin{array}{cccccc} 100 & 100 & 100 & 50 & 100 & 50 \\ 95 & 255 & 100 & 125 & 125 & 170 \\ 80 & 40 & 10 & 10 & 125 & 150 \\ 255 & 30 & 150 & 20 & 120 & 125 \\ 30 & 30 & 150 & 100 & 70 & 70 \\ 70 & 30 & 100 & 200 & 70 & 95 \end{array}\right] \text { max pooling } P_{2 \times 2}\left[\begin{array}{ccc} 255 & 125 & 170 \\ 255 & 150 & 150 \\ 70 & 200 & 95 \end{array}\right] \\ & \end{aligned} X1=⎣⎢⎢⎢⎢⎢⎢⎡1070255070352552550255152512510515010200100025010100201702510150950100701020060⎦⎥⎥⎥⎥⎥⎥⎤X2=⎣⎢⎢⎢⎢⎢⎢⎡1009580255307010025540303030100100101501501005012510201002001001251251207070501701501257095⎦⎥⎥⎥⎥⎥⎥⎤ max pooling P2×2⎣⎡2552557012515020017015095⎦⎤
- 池化减小了特征的数量,提高了计算效率:同时减少特征的数量也可以降低过拟合的程度。
# 池化操作几何表示
Image(filename='images/15_08.png', width=700)
重叠池化和非重叠池化:
同常使用的都是非重叠池化,如上图。当步长stride 小于 pooling size,则会发生重叠池化。重叠池化使用示例–论文
虽然对于很多的CNN网络结构而言,池化都是很重要的。但是一些CNN没有使用池化来降低特征维度,反而使用了步长为2的卷积层替代。
可以将步长为2的卷积层视为具有可学习权重参数的池化层(池化层不具有学习参数,没有权重和偏置单元)。
4.实现CNN
传统神经网络中最重要的操作是矩阵乘法。在卷积神经网络CNN中,这个操作被卷积操作替代,此外还出现了池化操作。
4.1处理多个输入和颜色通道
卷积层的传统实现期望的是一个3阶的张量作为输入,例如有一个三维数组 X N 1 × N 2 × C i n \boldsymbol{X}_{N_1\times N_2 \times C_{in}} XN1×N2×Cin。其中, C i n C_{in} Cin代表的是
输入通道的个数。比如输入的是三通道RGB图像,则 C i n = 3 C_{in}=3 Cin=3;如果输入的是灰度图像,则 C i n = 1 C_{in}=1 Cin=1。
读取图像文件:
当处理图像数据的时候,可以使用uint8数据类型将图像读取为NumPy数组,从而减小内存的占用(相较于使用int16, int32, int64);
uint8整数在【0, 255】范围,用于存储RGB图像信息是足够的。
# 使用Tensorflow读取图像数据
# import tensorflow as tf
# img_raw = tf.io.read_file('name.png')
# img = tf.image.decode_image(img_raw)
# print("image shape:", img_raw)
# 当在Tensorflow中构建模型和数据加载器的时候,建议使用tf.image
# import imageio
# img = imageio.imread('name.png')
# print("image shape:", img.shape)
# print("Number of channels:", img.shape[2])
# print("Image data type:", img.dtype)
这里通过对每个通道分别执行卷积运算,然后将结果相加,其中每个通道都有其对象的卷积核:
计算过程如下:
Given an example X n 1 × n 2 × C i n a kernel matrix W m 1 × m 2 × c i n , and bias value b ⇒ { Z Conv = ∑ c = 1 C in W [ : , : , c ] ∗ X [ : , : , c ] Pre-activation: Z = Z Conv + b C Feature map: A = ϕ ( Z ) \begin{aligned} &\text { Given an example } \boldsymbol{X}_{n_{1} \times n_{2} \times C_{i n}} \\ &\text { a kernel matrix } \boldsymbol{W}_{m_{1} \times m_{2} \times c_{i n}}, \\ &\text { and bias value } b \end{aligned} \Rightarrow\left\{\begin{array}{l} \boldsymbol{Z}^{\text {Conv }}=\sum_{c=1}^{C_{\text {in }}} \boldsymbol{W}[:,:, c] * \boldsymbol{X}[:,:, c] \\ \begin{array}{l} \text { Pre-activation: } \quad \boldsymbol{Z}=\boldsymbol{Z}^{\text {Conv }}+b_{C} \\ \text { Feature map: } & \boldsymbol{A}=\phi(\boldsymbol{Z}) \end{array} \end{array}\right. Given an example Xn1×n2×Cin a kernel matrix Wm1×m2×cin, and bias value b⇒⎩⎨⎧ZConv =∑c=1Cin W[:,:,c]∗X[:,:,c] Pre-activation: Z=ZConv +bC Feature map: A=ϕ(Z)
这里最后的结果 A \boldsymbol{A} A为特征映射。CNN的一个卷积层可能又一个或者多个特征映射。
如果使用多个特征映射,则卷积核张量就变成了四个维度: w i d t h × h e i g h t × C i n × C o u t width\times height \times C_{in} \times C_{out} width×height×Cin×Cout,这里的width和height对应的是卷积核的size
C i n C_{in} Cin为输入通道的数量, C o u t C_{out} Cout为输出特征映射的数量。所以考虑了输出特征映射数量后,上面公式更新为:
Given an example X n 1 × n 2 × C i n ′ a kernel matrix W m 1 × m 2 × C in × C out , and bias vector b C out ⇒ { Z Conv [ : , : , k ] = ∑ c = 1 C in W [ : , : , c , k ] ∗ X [ : , : , c ] Z [ : , : , k ] = Z Conv [ : , : , k ] + b [ k ] A [ : , : , k ] = ϕ ( Z [ : , : , k ] ) \begin{aligned} &\text { Given an example } \boldsymbol{X}_{n_{1} \times n_{2} \times C_{i n}^{\prime}} \\ &\text { a kernel matrix } \boldsymbol{W}_{m_{1} \times m_{2} \times C_{\text {in }} \times C_{\text {out }}}, \\ &\text { and bias vector } \boldsymbol{b}_{C_{\text {out }}} \end{aligned} \Rightarrow\left\{\begin{array}{l} \boldsymbol{Z}^{\text {Conv }}[:,:, k]=\sum_{c=1}^{C_{\text {in }}} \boldsymbol{W}[:,:, c, k] * \boldsymbol{X}[:,:, c] \\ \boldsymbol{Z}[:,:, k]=\boldsymbol{Z}^{\operatorname{Conv}}[:,:, k]+b[k] \\ \boldsymbol{A}[:,:, k]=\phi(\boldsymbol{Z}[:,:, k]) \end{array}\right. Given an example Xn1×n2×Cin′ a kernel matrix Wm1×m2×Cin ×Cout , and bias vector bCout ⇒⎩⎨⎧ZConv [:,:,k]=∑c=1Cin W[:,:,c,k]∗X[:,:,c]Z[:,:,k]=ZConv[:,:,k]+b[k]A[:,:,k]=ϕ(Z[:,:,k])
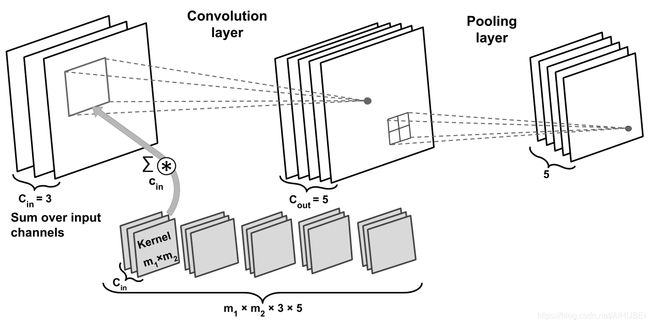
下图显示了:卷积层、池化层;其具有3个输入通道;卷积核张量为4维;卷积核size为 m 1 × m 2 m_1\times m_2 m1×m2,且有三个,分别对应三个输入通道;
总共有5组卷积核,这就导致最后有5个特征映射输出;
总共有5个池化层,用于对特征映射进行子采样;
Image(filename='images/15_09.png', width=800)
4.2计算参数个数
为了显示出卷积运算的优势:局部连接和参数共享,这里计算参数个数。
上图中,卷积张量是4维的,所以有 m 1 × m 2 × 3 × 5 m_1\times m_2 \times 3\times5 m1×m2×3×5个参数与卷积核相关联;
对卷积层中的每个输出特征映射,均具有偏置向量,所以偏置向量的size为5;
池化层没有任何的可训练或学习参数,因此整体如下:
m 1 × m 2 × 3 × 5 + 5 m_{1} \times m_{2} \times 3 \times 5+5 m1×m2×3×5+5
假定,使用的是same mode 填充模式,输入张量的size为 n 1 × n 2 × 3 n_{1} \times n_{2} \times 3 n1×n2×3, 则对应的输出特征映射size为 n 1 × n 2 × 5 n_{1} \times n_{2} \times 5 n1×n2×5
如果,使用的是全连接而非卷积操作,则使得权重矩阵达到相同数量的输出单元,所具有的参数个数为:
( n 1 × n 2 × 3 ) × ( n 1 × n 2 × 5 ) = ( n 1 × n 2 ) 2 × 3 × 5 \left(n_{1} \times n_{2} \times 3\right) \times\left(n_{1} \times n_{2} \times 5\right)=\left(n_{1} \times n_{2}\right)^{2} \times 3 \times 5 (n1×n2×3)×(n1×n2×5)=(n1×n2)2×3×5
此外,偏置向量的size为 n 1 × n 2 × 5 n_1\times n_2 \times 5 n1×n2×5。
读入图像数据:
import tensorflow as tf
img_raw = tf.io.read_file('example-image.png')
img = tf.image.decode_image(img_raw)
print('Image shape:', img.shape)
print('Number of channels:', img.shape[2])
print('Image data type:', img.dtype)
print(img[100:102, 100:102, :])
Image shape: (252, 221, 3)
Number of channels: 3
Image data type:
tf.Tensor(
[[[179 134 110]
[182 136 112]]
[[180 135 111]
[182 137 113]]], shape=(2, 2, 3), dtype=uint8)
import imageio
"""
这个就很快
"""
img = imageio.imread('example-image.png')
print('Image shape:', img.shape)
print('Number of channels:', img.shape[2])
print('Image data type:', img.dtype)
print(img[100:102, 100:102, :])
Image shape: (252, 221, 3)
Number of channels: 3
Image data type: uint8
[[[179 134 110]
[182 136 112]]
[[180 135 111]
[182 137 113]]]
输入图像的rank阶数:
img_raw = tf.io.read_file('example-image-gray.png')
img = tf.image.decode_image(img_raw)
tf.print('Rank:', tf.rank(img))
tf.print('Shape:', img.shape)
Rank: 3
Shape: TensorShape([252, 221, 1])
img = imageio.imread('example-image-gray.png')
tf.print('Rank:', tf.rank(img))
tf.print('Shape:', img.shape)
img_reshaped = tf.reshape(img, (img.shape[0], img.shape[1], 1))
tf.print('New Shape:', img_reshaped.shape)
tf.print('rank:', tf.rank(img_reshaped))
Rank: 2
Shape: (252, 221)
New Shape: TensorShape([252, 221, 1])
rank: 3
5.使用dropout对网络施加正则化
在实际任务中,我们很难真正确定一个网络的体量,结构太简单则容易欠拟合,结构太复杂又容易过拟合。解决这个问题的一种方法是构建一个容量
相对较大的网络(实际上,可以选择略大于实际所需的capacity),以在训练数据集上做得很好。然后,为了防止过拟合,可以采用一种或多种正则化
方案,以在新数据(如坚持的测试数据集)上获得良好的泛化性能。
这里的capacity指的是:网络的容量,即NN可以学习复杂函数,并进行逼近的一种程度;
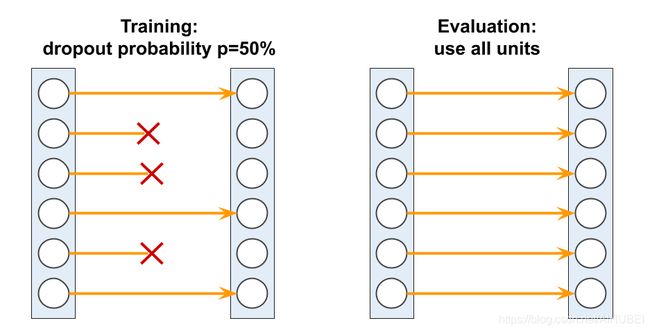
# 随机dropout可以有效防止过拟合,下图展示了一个P为0.5的例子。
# 在训练过程中,会有一半的神经元将被随机丢弃,在预测过程中,所有的神经元将被用于计算下一层的净活性值
Image(filename='images/15_10.png', width=700)
dropout作为一种正则化手段,目前使用非常广泛,非常流行。在深度神经网络中被用于避免过拟合。
dropout通常用于较高层的隐藏单元,工作原理为:在神经网络的训练阶段,每次迭代的时候随机丢弃一部分隐藏单元,概率为 P d r o p P_{drop} Pdrop。
丢弃神经元的概率为一个超参数,通常可设置为 P = 0.5 P=0.5 P=0.5。当减少一定比例的输入神经元,则与剩余神经元相关的权重会被重新调整,以解释丢弃的神经元。
机器学习中常用的正则化手段为:L1和L2正则化,其通常被用于处理模型的过拟合。
L1和L2正则化也可以用于NN,尤其是L2正则化相较于L1正则化可能使用的更加频繁,但在NN中海油其他的方法,比如丢弃法dropout。
下面的代码示例,对于全连接网络施加L2正则化,使用到的工具为kernel_regularizer,可以对特定层使用。
from tensorflow import keras
conv_layer = keras.layers.Conv2D(
filters=16, kernel_size=(3, 3),
kernel_regularizer=keras.regularizers.l2(0.001))
fc_layer = keras.layers.Dense(
units=16, kernel_regularizer=keras.regularizers.l2(0.001))
随机丢弃一部分神经元之后,网络被迫学习数据的冗余表示。毕竟一些神经元会被随机丢弃,因此网络不能依赖于任何一组隐藏单元,因而网络会从数据中学习
更具一般性和更加健壮的模式。
注意:神经元仅仅会在训练期间以一定概率被随机丢弃,而在模型评估期间,所有的神经元都必须是激活状态的。
由于在进行预测的时候经常去scale activations是不方便的,因此Tensorflow和其他工具则在训练期间进行scale activations操作。
比如:当设置了dropout概率为0.5的时候,就将activations增加一倍。这种方法通常被称为inverse dropout。
dropout与集成学习思想:
在深度学习中,无论是训练多个模型还是综合平均多个模型预测结果,它都具有昂贵的计算代价。
dropout实际上提供了一种变通方案,它可以同时训练多个模型,并在测试或预测的时候计算各模型的平均结果。虽然这种关系并不明显;
尽管模型融合与dropout的关系没有那么直接,但是考虑到dropout,在每次前向传递的时候以一定的概率随即将一些权值设置为零,即随机丢弃了一部分神经
元,这也就类似于对每个mini-batch都有着不同的模型。然后通过小批量的迭代,本质上我们是对 M = 2 h M = 2^h M=2h个模型进行了抽样。其中 h h h为隐层单元个数。
在模型推断期间(如,预测测试数据集中的标签),对在训练期间采样的不同模型进行平均,但计算代价可能比较大。
对模型进行平均,也就是计算模型 i i i返回的样本类别隶属概率值的几何平均值,计算过程如下:
p Ensemble = [ ∏ j = 1 M p { i } ] 1 M p_{\text {Ensemble }}=\left[\prod_{j=1}^{M} p^{\{i\}}\right]^{\frac{1}{M}} pEnsemble =[j=1∏Mp{i}]M1
这样一来,结合集成学习对dropout的解释如下:
可以通过将训练期间采样得到的最后(或者最终)模型的预测结果缩放 1 ( 1 − p ) \frac{1}{(1-p)} (1−p)1倍来近似集成模型(这里是M个模型)的几何平均值(Geometric mean)。
这样计算就相对于上面的公式计算具有更低的复杂度。
6.用于分类模型的损失函数
首先说一下激活函数,如RELU、sigmoid、tanh等;
RELU激活函数主要用于NN的中间层(隐层),进而引入模型的非线性特性;
sigmoid激活函数(用于二分类),softmax激活函数(用于多分类),主要用于最后(输出)层;他们的使用将会得到每条样本隶属于特定类别的概率。
Binary cross-entropy用于二分类(具有单一输出单元)的损失函数;
categorical cross-entropy用于多分类的损失函数;
Keras API对categorical cross-entropy提供了两个选项,这取决于真实类别标签使用的是独热编码还是整数标签,Keras中,整数标签也被称为sparse稀疏
-
BinaryCrossentropy()from_logits=Falsefrom_logits=True
-
CategoricalCrossentropy()from_logits=Falsefrom_logits=True
-
SparseCategoricalCrossentropy()from_logits=Falsefrom_logits=True
"""
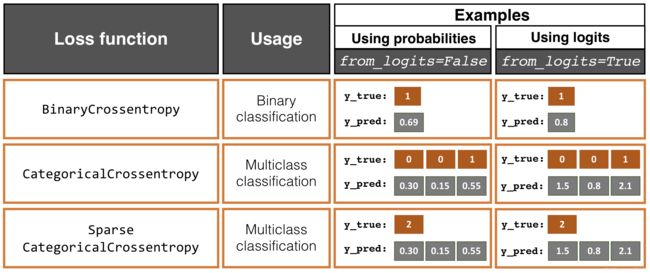
下图是Keras提供的损失函数,即二分类和多分类(类别标签为独热编码和整数(稀疏sparse)标签)。
这几个损失函数都可以选择输出几率logits或者概率;
"""
Image(filename='images/15_11.png', width=800)
####### Binary Crossentropy 二分类
bce_probas = tf.keras.losses.BinaryCrossentropy(from_logits=False)
bce_logits = tf.keras.losses.BinaryCrossentropy(from_logits=True)
logits = tf.constant([0.8])
probas = tf.keras.activations.sigmoid(logits)
tf.print(
'BCE (w Probas): {:.4f}'.format(
bce_probas(y_true=[1], y_pred=probas)),
'(w Logits): {:.4f}'.format(
bce_logits(y_true=[1], y_pred=logits)))
####### Categorical Crossentropy多分类,类别标签为独热编码
cce_probas = tf.keras.losses.CategoricalCrossentropy(
from_logits=False)
cce_logits = tf.keras.losses.CategoricalCrossentropy(
from_logits=True)
logits = tf.constant([[1.5, 0.8, 2.1]])
probas = tf.keras.activations.softmax(logits)
tf.print(
'CCE (w Probas): {:.4f}'.format(
cce_probas(y_true=[0, 0, 1], y_pred=probas)),
'(w Logits): {:.4f}'.format(
cce_logits(y_true=[0, 0, 1], y_pred=logits)))
####### Sparse Categorical Crossentropy多分类,类别标签为整数(sparseb)
sp_cce_probas = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=False)
sp_cce_logits = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True)
tf.print(
'Sparse CCE (w Probas): {:.4f}'.format(
sp_cce_probas(y_true=[2], y_pred=probas)),
'(w Logits): {:.4f}'.format(
sp_cce_logits(y_true=[2], y_pred=logits)))
BCE (w Probas): 0.3711 (w Logits): 0.3711
CCE (w Probas): 0.5996 (w Logits): 0.5996
Sparse CCE (w Probas): 0.5996 (w Logits): 0.5996
有时候会出现使用categorical cross-entropy损失函数作为二分类问题的损失函数。
通常对于二分类任务,最终会得到单一输出结果,且将其作为样本预测为正的概率,因此无需第二个输出,结合该输出值,可以计算出样本负类别的概率。
但有时候,我们需要得到每一个样本的两个输出,即分别属于正负类别的概率,这时候使用softmax作为激活函数更合适,以至于实现了结果的归一化输出
即结果之和为1.这种情况下,使用categorical cross-entropy就比较合适了。
7.使用TensorFlow实现深度卷积神经网络
7.1多层CNN的体系结构
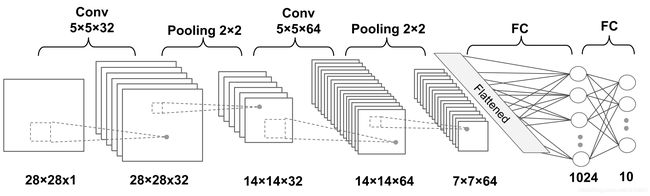
Image(filename='images/15_12.png', width=800)
网络输入为28x28的灰度图像,因此图像的通道数为1.所以输入张量的维数为: b a t c h s i z e × 28 × 28 × 1 batchsize\times 28 \times 28 \times 1 batchsize×28×28×1;
输入数据经过了2个卷积操作,卷积核size为 5 × 5 5\times 5 5×5。第一次卷积之后,有32个输出特征映射,第二次卷积之后,有64个输出特征映射;
每一个卷积层之后都紧接着有一个自采样层,这里是最大池化max-pooling,其中pooling size为 P 2 × 2 P_{2\times 2} P2×2。
紧接着两个全连接层,前一个全连接层将输出传递给第二个全连接层,第二个全连接层充当最后的Softmax输出层。
各层的维度表示如下:
- Input: batchsize × 28 × 28 × 1 \times 28 \times 28 \times 1 ×28×28×1
- Conv_1: batchsize × 28 × 28 × 32 \times 28 \times 28 \times 32 ×28×28×32
- Pooling_1: batchsize × 14 × 14 × 32 \times 14 \times 14 \times 32 ×14×14×32
- Conv_2: batchsize × 14 × 14 × 64 \times 14 \times 14 \times 64 ×14×14×64
- Pooling_2: batchsize × 7 × 7 × 64 \times 7 \times 7 \times 64 ×7×7×64
- FC_1: batchsize$ \times 1024$
- F C − 2 \mathrm{FC}_{-} 2 FC−2 and softmax layer: batchsize × 10 \times 10 ×10
对于卷积核,使用的步长为strides=1,以便于在生成的特征映射中保留输入数据的维度;
在池化层中,使用的步长为strides=2, 以便于对图像进行二次采样,并缩小输出特征映射的大小。下面的网络实现将使用Tensorflow Keras API.
7.2载入并预处理数据
import tensorflow_datasets as tfds
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
## MNIST dataset
mnist_bldr = tfds.builder('mnist')
mnist_bldr.download_and_prepare()
datasets = mnist_bldr.as_dataset(shuffle_files=False)
print(datasets.keys())
mnist_train_orig, mnist_test_orig = datasets['train'], datasets['test']
dict_keys(['test', 'train'])
MNIST数据集本身附带了预先指定的训练和测试数据集划分方案。但这里还是自行进行划分。即从训练集中拆分出验证集。
上面设置了shuffle_files=False,因为这里为了将训练集拆分为两部分,即较小的训练集和验证集数据。
如果没有设置shuffle_files=False,则每次获取一小批数据mini-batch的时候,都将会引起数据集的重新shuffle.
BUFFER_SIZE = 10000
BATCH_SIZE = 64
NUM_EPOCHS = 20
mnist_train = mnist_train_orig.map(
lambda item: (tf.cast(item['image'], tf.float32)/255.0,
tf.cast(item['label'], tf.int32)))
mnist_test = mnist_test_orig.map(
lambda item: (tf.cast(item['image'], tf.float32)/255.0,
tf.cast(item['label'], tf.int32)))
tf.random.set_seed(1)
mnist_train = mnist_train.shuffle(buffer_size=BUFFER_SIZE,
reshuffle_each_iteration=False)
mnist_valid = mnist_train.take(10000).batch(BATCH_SIZE)
mnist_train = mnist_train.skip(10000).batch(BATCH_SIZE)
7.3使用TensorFlow Keras API实现CNN
这里为了实现CNN,选择使用的是Keras Sequential类来实现将不同的layers堆叠起来,比如:卷积层、池化层、dropout、以及全连接层;
Keras layers提供了相应的实现类:
二维卷积:tf.keras.layers.Conv2D;
池化:tf.keras.layers.MaxPool2D
tf.keras.layers.AvgPool2D
丢弃法:tf.keras.layers.Dropout
7.4具体配置各个层次
-
Conv2D:
tf.keras.layers.Conv2Dfilterskernel_sizestridespadding
-
MaxPool2D:
tf.keras.layers.MaxPool2Dpool_sizestridespadding
-
Dropout
tf.keras.layers.Dropout2Drate
使用Conv2D类构建一个layer,需要指明卷积核的个数和size,其中,个数与输出特征映射个数相同;
其它用于配置卷积层的参数:
最常用的是步长strides、padding等;
7.5使用Keras搭建CNN
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(
filters=32, kernel_size=(5, 5),
strides=(1, 1), padding='same',
data_format='channels_last',
name='conv_1', activation='relu'))
model.add(tf.keras.layers.MaxPool2D(
pool_size=(2, 2), name='pool_1'))
model.add(tf.keras.layers.Conv2D(
filters=64, kernel_size=(5, 5),
strides=(1, 1), padding='same',
name='conv_2', activation='relu'))
model.add(tf.keras.layers.MaxPool2D(pool_size=(2, 2), name='pool_2'))
2个卷积层、卷积核size为 5 × 5 5\times 5 5×5、使用“same”padding;
最大池化max-pooling 的size为 2 × 2 2\times 2 2×2、步长为2、可以实现将维度减半;
# 利用Keras API计算特征映射的size
model.compute_output_shape(input_shape=(16, 28, 28, 1)) # 输入size: batch中图像数量、高、宽、通道数
TensorShape([16, 7, 7, 64])
结果表明,batch dimension为16, 特征size为7x7,通道数为64. 这里的16是随意使用,可以用None替代
# 需要添加的下一层为全连接层,但在此之前,需要先将前几层的输出平铺拉伸Flatten,从而满足全连接层的要求
model.add(tf.keras.layers.Flatten())
model.compute_output_shape(input_shape=(16, 28, 28, 1))
TensorShape([16, 3136])
从model.compute_output_shape的结果可以看出,前面的层次,即全连接层的输入维度已经成功建立;
添加全连接层,设置dropout层;
model.add(tf.keras.layers.Dense(
units=1024, name='fc_1',
activation='relu'))
model.add(tf.keras.layers.Dropout(
rate=0.5))
model.add(tf.keras.layers.Dense(
units=10, name='fc_2', # 对应MNIST数据集由10个class
activation='softmax')) # 使用softmax激活函数,得到每个样本的类成员资格(总和为1)
tf.random.set_seed(1)
model.build(input_shape=(None, 28, 28, 1)) # 调用build()方法创建后期变量,并编译模型
model.compute_output_shape(input_shape=(16, 28, 28, 1))
TensorShape([16, 10])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv_1 (Conv2D) multiple 832
_________________________________________________________________
pool_1 (MaxPooling2D) multiple 0
_________________________________________________________________
conv_2 (Conv2D) multiple 51264
_________________________________________________________________
pool_2 (MaxPooling2D) multiple 0
_________________________________________________________________
flatten (Flatten) multiple 0
_________________________________________________________________
fc_1 (Dense) multiple 3212288
_________________________________________________________________
dropout (Dropout) multiple 0
_________________________________________________________________
fc_2 (Dense) multiple 10250
_________________________________________________________________
fc_1 (Dense) multiple 11264
_________________________________________________________________
dropout_1 (Dropout) multiple 0
_________________________________________________________________
fc_2 (Dense) multiple 10250
=================================================================
Total params: 3,296,148
Trainable params: 3,296,148
Non-trainable params: 0
_________________________________________________________________
使用Adam优化算法,它是一种鲁棒的、基于梯度的优化方法,适用于非凸优化和机器学习问题。两种流行的优化方法启发了Adam: RMSProp和AdaGrad.
Adam的核心优势:从梯度矩的运行平均值中选择更新步长。Adam算法论文
其次,关于多分类损失函数的选择:多分类问题中的,整数(稀疏标签)----SparseCategoricalCrossentropy
多分类问题中,独热编码类别标签----one-hot encoded labels-----CategoricalCrossentropy
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy']) # same as `tf.keras.metrics.SparseCategoricalAccuracy(name='accuracy')`
history = model.fit(mnist_train, epochs=NUM_EPOCHS,
validation_data=mnist_valid,
shuffle=True)
Epoch 1/20
782/782 [==============================] - 16s 20ms/step - loss: 0.6741 - accuracy: 0.7535 - val_loss: 0.1106 - val_accuracy: 0.9771
Epoch 2/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0910 - accuracy: 0.9802 - val_loss: 0.0666 - val_accuracy: 0.9841
Epoch 3/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0562 - accuracy: 0.9869 - val_loss: 0.0689 - val_accuracy: 0.9851
Epoch 4/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0402 - accuracy: 0.9907 - val_loss: 0.0717 - val_accuracy: 0.9859
Epoch 5/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0341 - accuracy: 0.9913 - val_loss: 0.0529 - val_accuracy: 0.9890
Epoch 6/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0216 - accuracy: 0.9944 - val_loss: 0.0544 - val_accuracy: 0.9899
Epoch 7/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0240 - accuracy: 0.9937 - val_loss: 0.0546 - val_accuracy: 0.9882
Epoch 8/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0208 - accuracy: 0.9945 - val_loss: 0.0506 - val_accuracy: 0.9886
Epoch 9/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0166 - accuracy: 0.9957 - val_loss: 0.0569 - val_accuracy: 0.9889
Epoch 10/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0180 - accuracy: 0.9951 - val_loss: 0.0584 - val_accuracy: 0.9893
Epoch 11/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0149 - accuracy: 0.9963 - val_loss: 0.0476 - val_accuracy: 0.9915
Epoch 12/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0101 - accuracy: 0.9970 - val_loss: 0.0591 - val_accuracy: 0.9904
Epoch 13/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0119 - accuracy: 0.9966 - val_loss: 0.0562 - val_accuracy: 0.9903
Epoch 14/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0116 - accuracy: 0.9969 - val_loss: 0.0605 - val_accuracy: 0.9890
Epoch 15/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0128 - accuracy: 0.9966 - val_loss: 0.0481 - val_accuracy: 0.9915
Epoch 16/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0111 - accuracy: 0.9972 - val_loss: 0.0555 - val_accuracy: 0.9908
Epoch 17/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0103 - accuracy: 0.9974 - val_loss: 0.0645 - val_accuracy: 0.9911
Epoch 18/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0100 - accuracy: 0.9975 - val_loss: 0.0528 - val_accuracy: 0.9903
Epoch 19/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0087 - accuracy: 0.9978 - val_loss: 0.0609 - val_accuracy: 0.9910
Epoch 20/20
782/782 [==============================] - 8s 10ms/step - loss: 0.0068 - accuracy: 0.9983 - val_loss: 0.0586 - val_accuracy: 0.9904
hist = history.history
x_arr = np.arange(len(hist['loss'])) + 1
fig = plt.figure(figsize=(12, 4))
ax = fig.add_subplot(1, 2, 1)
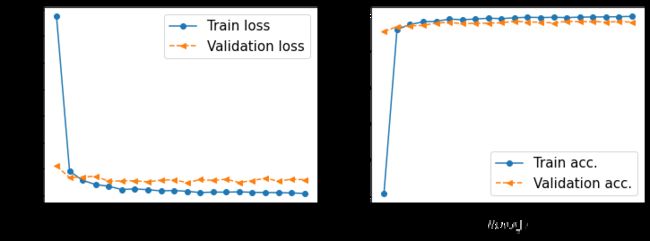
ax.plot(x_arr, hist['loss'], '-o', label='Train loss')
ax.plot(x_arr, hist['val_loss'], '--<', label='Validation loss')
ax.set_xlabel('Epoch', size=15)
ax.set_ylabel('Loss', size=15)
ax.legend(fontsize=15)
ax = fig.add_subplot(1, 2, 2)
ax.plot(x_arr, hist['accuracy'], '-o', label='Train acc.')
ax.plot(x_arr, hist['val_accuracy'], '--<', label='Validation acc.')
ax.legend(fontsize=15)
ax.set_xlabel('Epoch', size=15)
ax.set_ylabel('Accuracy', size=15)
#plt.savefig('figures/15_12.png', dpi=300)
plt.show()
# 通过调用.evaluate()方法在测试数据集上评估训练好的模型
test_results = model.evaluate(mnist_test.batch(20))
print('\nTest Acc. {:.2f}%'.format(test_results[1]*100))
500/Unknown - 2s 4ms/step - loss: 0.0547 - accuracy: 0.9898
Test Acc. 98.98%
batch_test = next(iter(mnist_test.batch(12)))
preds = model(batch_test[0])
tf.print(preds.shape)
preds = tf.argmax(preds, axis=1)
print(preds)
fig = plt.figure(figsize=(12, 4))
for i in range(12):
ax = fig.add_subplot(2, 6, i+1)
ax.set_xticks([]); ax.set_yticks([])
img = batch_test[0][i, :, :, 0]
ax.imshow(img, cmap='gray_r')
ax.text(0.9, 0.1, '{}'.format(preds[i]),
size=15, color='blue',
horizontalalignment='center',
verticalalignment='center',
transform=ax.transAxes)
#plt.savefig('figures/15_13.png', dpi=300)
plt.show()
TensorShape([12, 10])
tf.Tensor([2 0 4 8 7 6 0 6 3 1 8 0], shape=(12,), dtype=int64)
import os
if not os.path.exists('./models'):
os.mkdir('models')
model.save('models/mnist-cnn.h5')