「数字电子技术基础」7.时序逻辑电路
目录
- 绪论
-
- 一般结构
- 分类
- 时序电路的分析方法
-
- 同步时序电路的分析步骤
- 异步时序电路的分析步骤
- 计数器
-
- 集成同步加法计数器
-
- 计数器的级联
-
- 同步并行进位
- 异步串行进位
- 利用集成加法计数器构造任意进制的计数器
-
- 由大容量计数器构造小容量计数器
-
- 清零法
- 置数法
- 由小容量计数器构造大容量计数器
- 集成异步加法计数器
-
- 2/5分频
- 2/8分频
- 集成异步加法计数器的正常打开方式
- 集成异步加法计数器的特殊打开方式
- 清零问题
- 集成加/减计数器
- 同步时序逻辑电路的设计
- 寄存器及移位寄存器型计数器
-
- 环形计数器
- 扭环形计数器
绪论
一般结构
时序逻辑电路和组合逻辑电路的区别就在于,时序逻辑电路的输出不仅取决于当前的输入,还取决于当前电路的状态甚至之前电路的状态。也就是说时序逻辑电路有某一个反馈/存储结构。

因此可以用三组方程来描述一个时序逻辑电路:
- 输出方程。也就是输出变量和输入变量、状态变量的关系
- 驱动方程。也就是存储电路的输入量的函数
- 状态方程。也就是存储电路的输出量的函数
因此,研究时序逻辑电路也就是研究这三组方程。
分类
首先根据电路中时钟信号是否统一,可以将电路分为同步时序电路和异步时序电路。看电路图可以很容易分辨,如果所有的clk端口都接到同样的cp,说明是同步。否则是异步。
然后根据输出是否和当前时刻的输入有关,又将电路分成了Mealy型和Moore型。Mealy型电路输出不仅和状态Q相关,还和输入X相关,本质上是异步输出,当X改变时,输出也改变。但电路可能仍然是同步电路 Moore型电路输出只和状态Q相关,是同步输出。但电路可能仍然是异步电路
时序电路的分析方法
同步时序电路的分析步骤
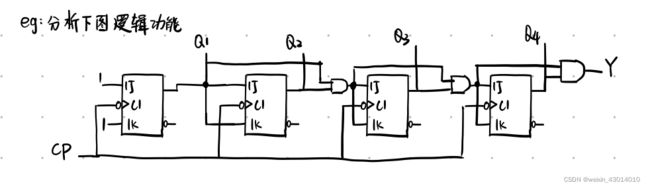
1.写时钟方程、驱动方程 \colorbox{gray}{\color{white}{1.写时钟方程、驱动方程}} 1.写时钟方程、驱动方程
也就是确定每一个触发器什么时候动作(时钟方程)、影响触发器功能的变量是什么(驱动方程)
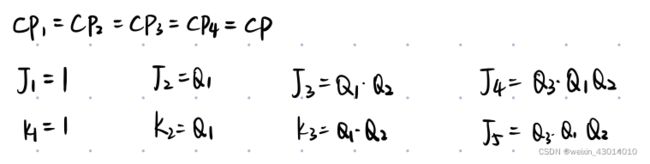
2.写输出方程 \colorbox{gray}{\color{white}{2.写输出方程}} 2.写输出方程
注意有些电路是没有输出的,或者输出就是电路的状态,那就可以略过这一步了。
Y = Q 4 Q 3 Q 2 Q 1 Y=Q_4Q_3Q_2Q_1 Y=Q4Q3Q2Q1
3.写状态方程 \colorbox{gray}{\color{white}{3.写状态方程}} 3.写状态方程
也就是确定触发器具体怎么动作
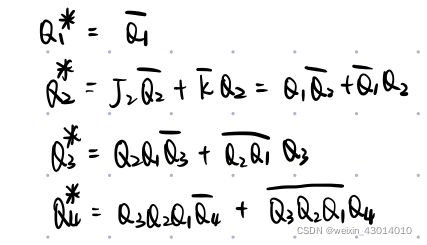
4.列状态转换表并画状态转换图 \colorbox{gray}{\color{white}{4.列状态转换表并画状态转换图}} 4.列状态转换表并画状态转换图
顺着状态方程写就可以,从原态计算出次态。

状态转换图画的是原态,也可以叫做现态。
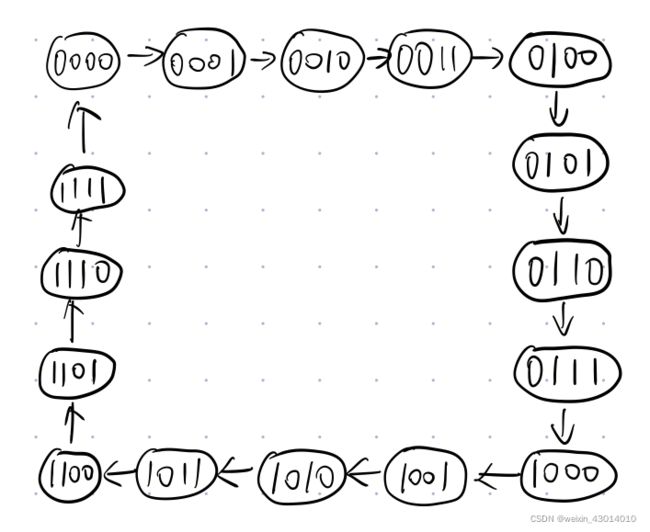
5.判断逻辑功能,检查自启动 \colorbox{gray}{\color{white}{5.判断逻辑功能,检查自启动}} 5.判断逻辑功能,检查自启动
四个状态从0000随着时钟变到了1111,然后循环,输出Y每循环一圈输出一次高电平,可以看作是同步4位二进制加法计数器
可以自启动(因为只有一个圈,不论初态落在哪里都可以进入有效循环)
异步时序电路的分析步骤
异步时序电路分析主要需要注意的点是,时钟方程不再是统一的了,每一个触发器会在不同的时刻被激活动作。我们还是以一个例题来讲解。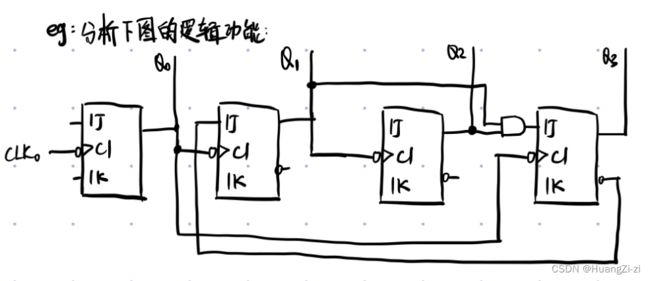
1.写时钟方程、驱动方程 \colorbox{gray}{\color{white}{1.写时钟方程、驱动方程}} 1.写时钟方程、驱动方程
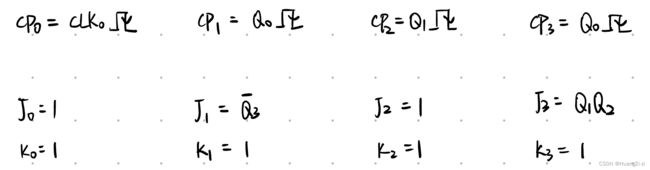
2.写状态方程 \colorbox{gray}{\color{white}{2.写状态方程}} 2.写状态方程
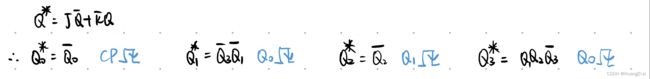
3.列状态转换表、画状态转换图 \colorbox{gray}{\color{white}{3.列状态转换表、画状态转换图}} 3.列状态转换表、画状态转换图
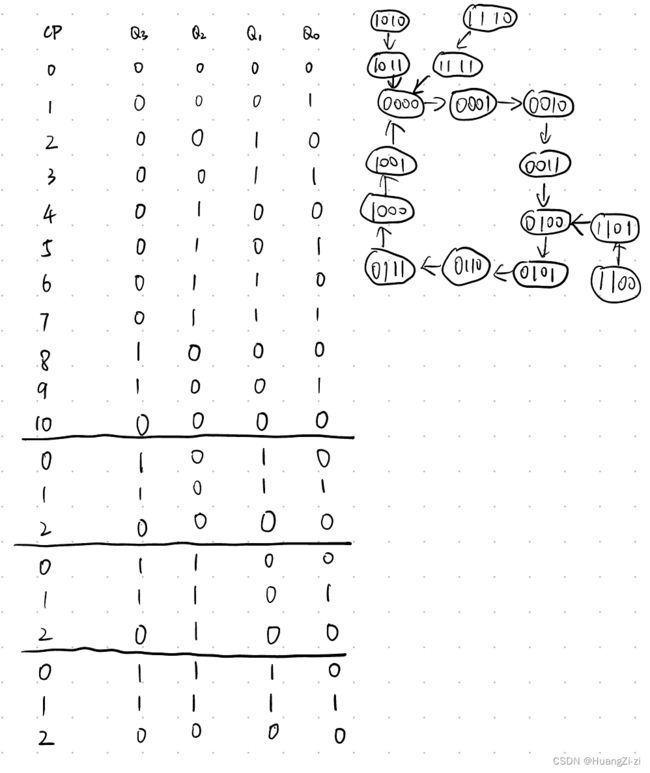
4.判断逻辑功能、检查自启动 \colorbox{gray}{\color{white}{4.判断逻辑功能、检查自启动}} 4.判断逻辑功能、检查自启动
该电路为异步10进制加法计数器,可以自启动
计数器
刚才的两个例子,都是构成的计数器。这里再详细讲一点。计数器,也就是计时钟脉冲个数的器件。在时序电路里面有很多作用比如定时,分频等等。
计数器应该具有的功能有:计数、保持、清零、置数
集成同步加法计数器

在考卷上应该会出现74LS160、74HC162这样的字样,前面的都是类型代号,只要后面三位数字相同,逻辑功能就是相同的。具体的使用方法参看本文后面的例题。
功能描述:CR,LD输入有效电平,如果是异步就立刻完成操作,如果是同步则需要等待时钟脉冲时完成操作。使能端EP,ET,接成11计数,有0就是保持,而01的保持和11的保持和00的保持是不一样的,可以看下面的描述。

计数器的级联
同步并行进位

所谓同步并行进位,也就是所有计数器都接入同一个时钟。但是后面计数器的使能计数端接在前面计数器的进位输出上,也就是只有前面计数器进位,后面的计数器才能计数。在这个过程中,前面计数器和后面计数器是同时计数的,所以叫做同步并行进位。
异步串行进位
同样是1000进制,现在我们用异步电路实现
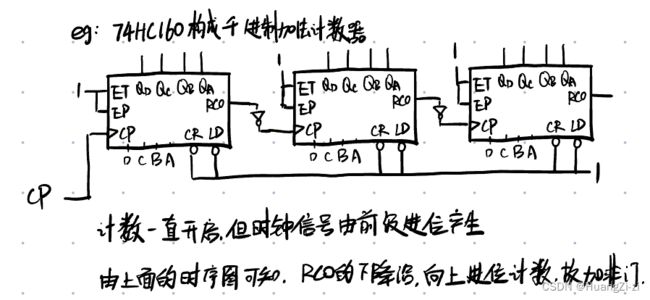
计数器计数需要两个条件,第一是使能为计数,第二是有时钟脉冲。之前同步电路是控制使能端,而异步电路则是控制时钟脉冲。
只有当前一个计数器进位时输出一个脉冲使得后面计数器进行计数,其他时刻虽然后面计数器处于计数状态,但是没有时钟,所以不计数。
这里RCO连接到后面的CP端口接了非门,因为RCO的特性是正常低电平,在计到9(15)的时刻变成高电平,在进位的时刻(9->0,15->0时)变成低电平。而观察CP端口前并没有非号,所以为上升沿触发,所以需要反相使用。
利用集成加法计数器构造任意进制的计数器
由大容量计数器构造小容量计数器
总体思路是跑到某一个地方要让计数器回来。比如本来从0000->1111,但是现在我只需要5个状态,那么0100的时候就应该回来,不能再向0101继续计数了。
清零法
清零法又分为异步清零法和同步清零法。选用那种由计数器的特性决定,如果是160161,则都是异步清零,162163则是同步。
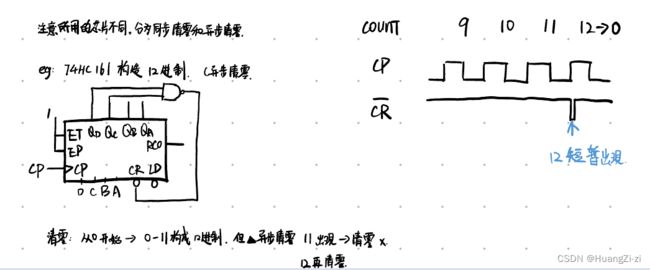
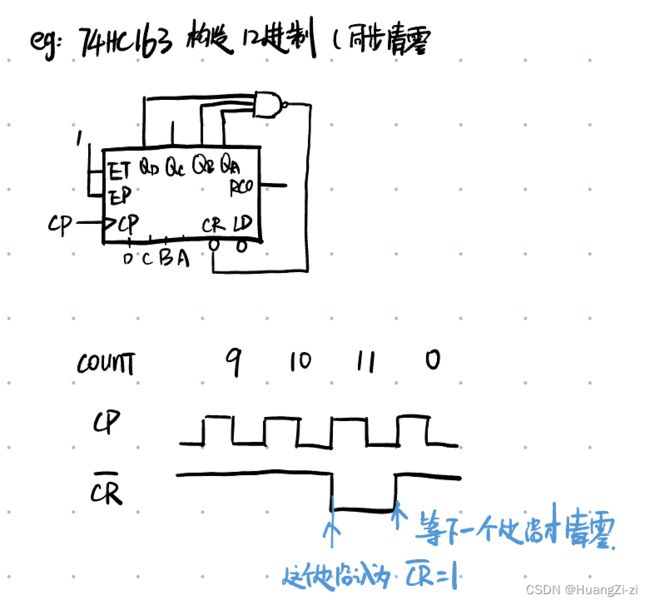
设计计数器时一定要注意咱们数状态的个数而不要按8421的权重计算数字的大小。比如12进制,就是有12个状态,要是从0000开始那就是到1011,要是从0001开始就是1100。
由于异步清零是出现清零信号马上清零。如果从0000开始,在1011清零,当计数器输出1100时,触发清零,然后回到0000,那么最后一个状态就只是一闪而过,并不能算做有效的一个状态,所以需要多进一位,从0000开始,在1100清零。1100虽然出现,但只有一个瞬间,马上就被清零了。
当计数器是同步清零的时候,不仅要求清零信号有效,还要求是在时钟触发的条件下才能清零。由于电路具有延迟,在 C R ‾ {\overline{CR}} CR下降沿同时刻的时钟信号还不能引起清零,所以最后一个状态1011可以保持到下一个时钟周期,此时当时钟脉冲到来,完成清零。所以从0000开始,到1011时返回就可以
这里补充讲解一下全译码和半译码。还是很好理解的。一般设计都采用半译码,这样比较简洁。
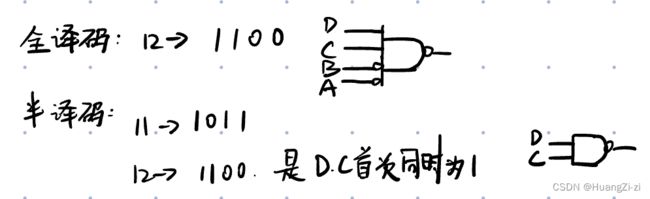
置数法
就是运用置数功能,当计到某一个数时触发置数,把数据输入端的数字置入。如果置入0000那么和同步清零是一样的效果。如果置入一些其他的数,则可以变换不同的编码。

由小容量计数器构造大容量计数器
首先级联,将小容量的计数器扩展成大容量的计数器,再运用上文的方法,通过清零或者置数构造任意进制。
集成异步加法计数器
所谓异步,说白了就是有两个计数器封装在同一片芯片里,因为通用EP、ET控制端,只能通过异步的方法级联。
2/5分频
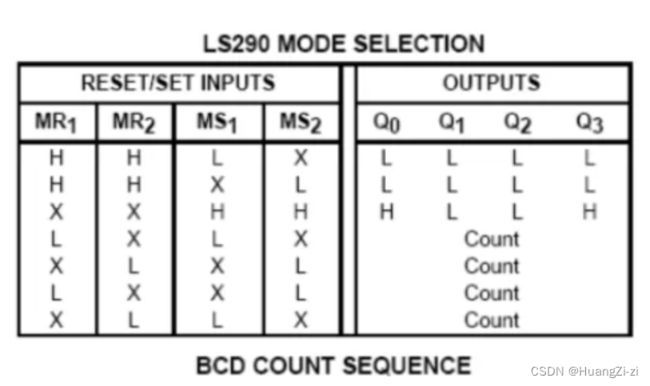
74HC90和74HC290,两个芯片逻辑功能相同,引脚排列不同
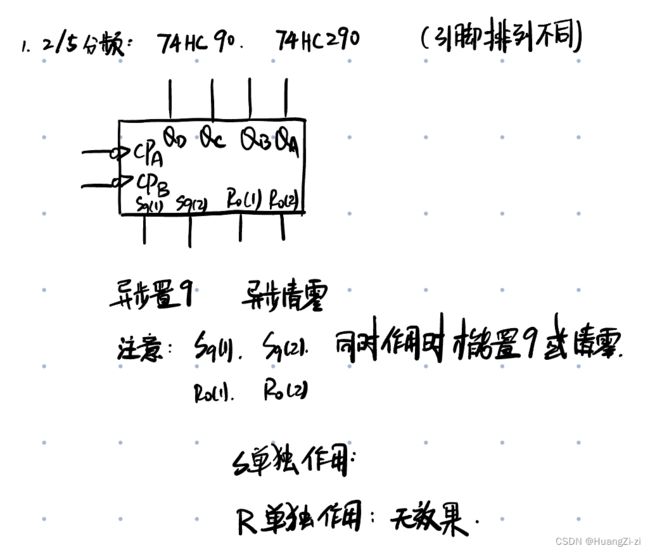
从CPA输入,对应QA输出,二分频。从CPB输入,对应QDQCQB输出,5分频。
这种电路的的运用会比较灵活,但是一定注意一点,不管是清零还是置九,都要求两个输入端同时有效,否则计数器会继续计数说白了就是不会出现只清零一半这种情况
2/8分频
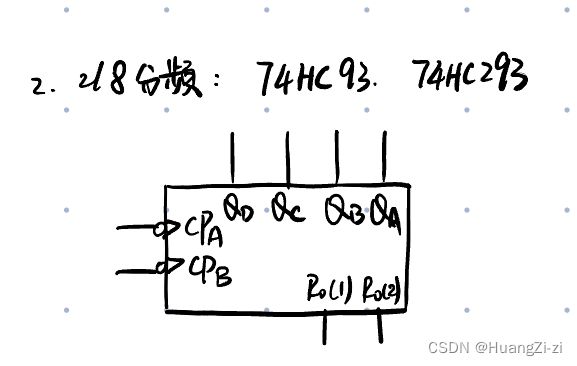
2/5分频实际上是10进制,而2/8分频就是16进制了。这个芯片会简单一点,因为除了清零之外没有什么数字可以置进去了。
集成异步加法计数器的正常打开方式

最最正常的打开方式是从CPA输入,这样QA会在01之间跳变,形成二分频。然后把二分频后的信号接入CPB,进行5进制计数,最后就能得到0000->1001的循环,构成十进制计数器。
如果外部时钟从CPB接入,这样QD构成5分频,如果把QD接入CPA,同样能够得到十进制计数器,不过读数的时候,QA就得是最高位了,然后依次BCD
集成异步加法计数器的特殊打开方式

虽然电路没有变,但是编码方式改变后,电路的逻辑功能就发生了改变。如果把一些奇怪的东西接入时钟,则会有更加意想不到的收获,本文就不再深入讨论了。
清零问题
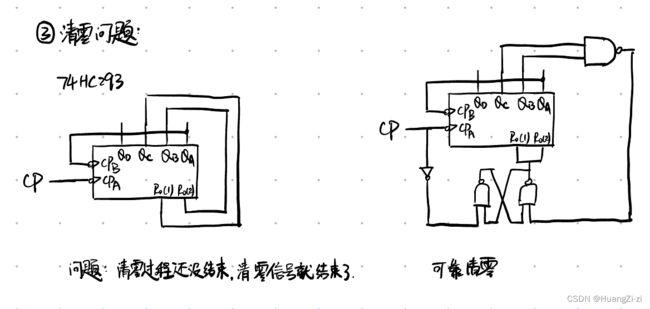
问题在于,用了多个计数器的输出来对多个计数器进行清零。任意一个计数器清零成功,输出改变,则清零信号就消失,如果此时由于延迟等因素另一个计数器还没有清零,就不再有清零机会了。所以使用一个锁存器,把输出的清零信号延展成半个时钟周期的长信号,保证清零成功后清零信号才消失。
首先插播一条对于SR锁存器的解释。由与非门构成的锁存器,本身对应的输入应该是 S D ‾ \overline{S_D} SD和 R D ‾ \overline{R_D} RD,但是现在我们把左边加上非门,右边与非门拆成与门和非门来看,也就是两个输入端变成了我们熟悉的RD和SD。满足SR=0的时候,某一侧的输出就是这一侧的输入。不满足SR=0就是禁态,两边都输出1。
分析一下这个电路,当清零有效时,锁存器右边输入1,左边输入0(因为电路在CP下降沿动作,清零信号出现在下降沿传输延迟之后,此时CP为低电平)。满足SR=0的条件,右边输出等于右边输入(1),产生清零信号。清零后右边输入变为0,此时处于保持状态,继续输出1,达到了延展短信号的目的。等到CP迎来上升沿,左边输入1,右边输入0,满足SR=0的条件,右边输出等于右边输入(0),清零结束,进入下一轮的计数。
集成加/减计数器
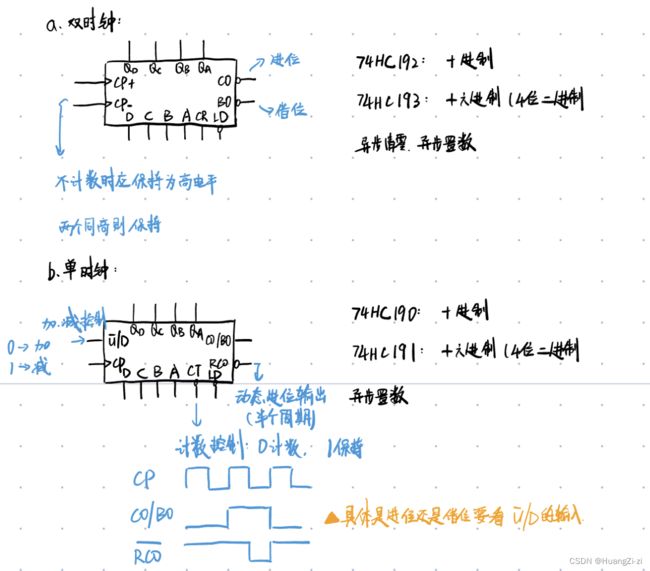
其实思路也很简单。就是要通过某一个输入来区分加法还是减法。第一个是可以用不同的时钟输入,第二个是可以增加单独的标志位。
在看190/191芯片的时候发现除了正常的CO/BO输出之外还多了一个 R C O ‾ \overline{RCO} RCO
首先,RCO是什么?RCO是ripple carry output的缩写。中文名动态进位输出。具体的时序可以参考上面的手绘时序图。

同步时序逻辑电路的设计
通过一道例题来讲解设计的步骤吧
eg:用D触发器设计5进制计数器。要求:循环计数、输出状态,不需要其他输入输出
1.确定输入变量、输出变量、状态个数 \colorbox{gray}{\color{white}1.确定输入变量、输出变量、状态个数} 1.确定输入变量、输出变量、状态个数
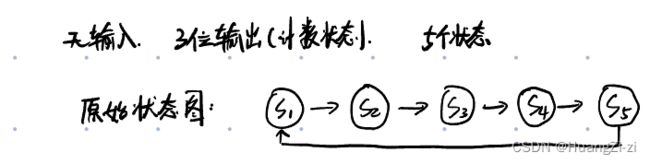
2.状态化简 \colorbox{gray}{\color{white}2.状态化简} 2.状态化简
这道题没有化简的空间,这一步就跳过了
3.状态分配 \colorbox{gray}{\color{white}3.状态分配} 3.状态分配
也就是进行编码,将不同的状态用最小项表示出来

状态分配结束之后可以根据之前画的原始状态转换图,写成状态转换表。至于无效状态,一般我们不关心它的次态,但是值得注意的是:不关心无效态的次态可能导致电路无法自启动。具体什么情况呢,这个例子就会涉及。
4.选触发器,确定相应方程 \colorbox{gray}{\color{white}4.选触发器,确定相应方程} 4.选触发器,确定相应方程
就是和触发器相关的一系列方程就都要确定了,包括时钟方程、状态方程、驱动方程、输出方程

设计同步时序电路,所以时钟方程可以不写。而本题没有要求输出,所以输出方程也可以不写。
5.自启动检查 \colorbox{gray}{\color{white}5.自启动检查} 5.自启动检查
前面已经求了状态方程,根据这个就可以写出完整的状态转换图。由于前面给所有任意项都是不关心,也就导致可能在任意项之间的相互转换会落入小循环导致电路无法自启动。当出现无法自启动的时候再修改就是一个比较“灵性”的问题了。
一般修改的思路就是从无法自启动的那个小循环着手。比如本题的100->100。我们让100的次态不再是100不就可以了吗?这个时候看看卡诺图有没有别的圈可以圈,一般就可以改正问题了。
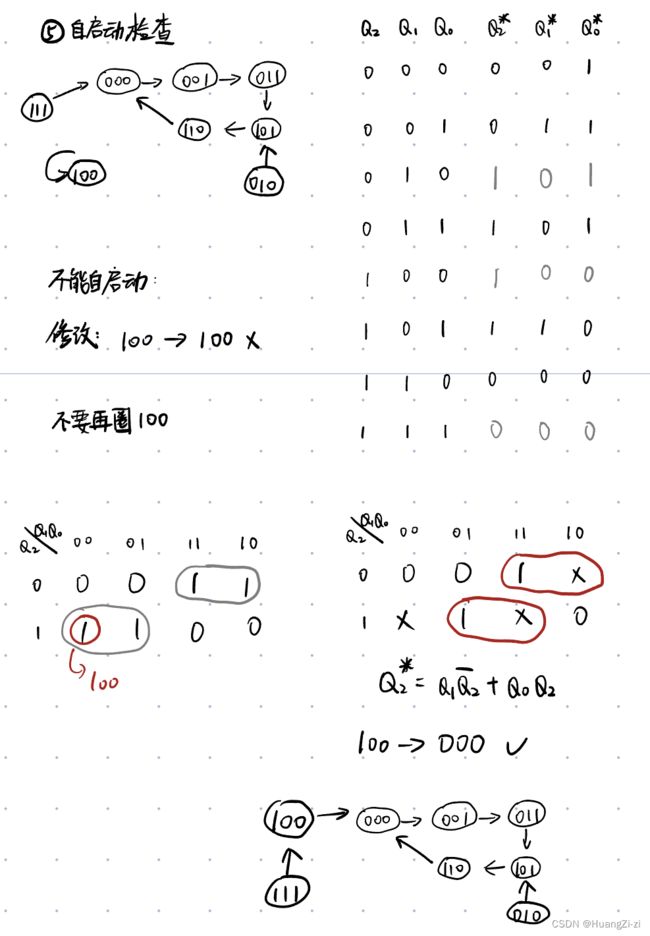
如果想要避免设计出来以后出现无法自启动额情况,还可以从源头着手,对于任意项,我们可以随意分配一个次态。比如我不需要111,但是我不能让它继续是XXX的任意态,而是让它的次态回到000,这样所有状态都有明确的次态,就一定可以自启动了。但是这样的设计过程又会引起电路复杂。如果题目要求用最简单的方式完成设计,就只能把所以多余状态当作任意项对待。
6.画电路图 \colorbox{gray}{\color{white}6.画电路图} 6.画电路图

刚才的例子是没有化简这一步的,然而恰好化简这一步是非常重要的一步,所以在这里再补充一道例题。
eg:设计一个数字密码锁,要求连续输入3个或3个以上的“1”时锁打开,否则锁关闭
这个密码锁要求能辨别连续输入3个及以上的1,所以应该具有4个状态。也就是(连续)0个、1个、2个、3个及以上,这样就能画出原始状态转换图了。
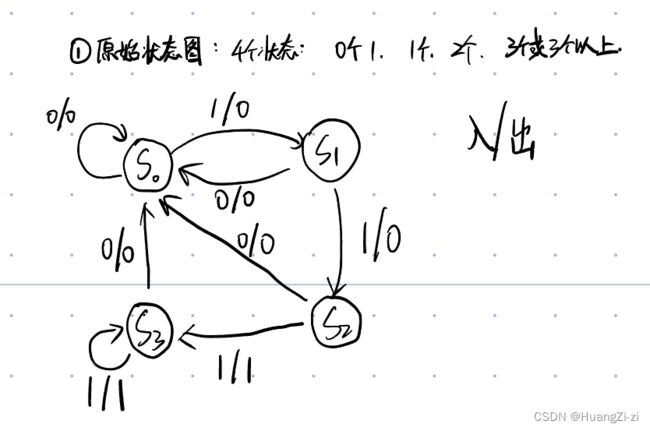
在讲解化简之前首先需要讲一下什么是等价状态。等价状态是指
- 在相同的输入情况下有相同的输出
- 转化到相同的次态
我们进行化简的对象就是等价状态。
看上图,S2输入1输出1,转换到S3,输入0输出0,转换到S0。S3输入1输出1,转换到S3,输入0输出0,转换到S0。说明他们是等价的。

对于等价状态,可以删去多余的,只保留一个,所谓的化简也就是这样了,减少状态个数,可以减少触发器的个数。(虽然本题没有达到减少触发器个数的目的,但还是减少了状态个数的)


寄存器及移位寄存器型计数器
寄存器,用来储存的。储存的内容是一组二进制代码。数码寄存器应该具有寄存数码、清除的功能。如果在此之外还有移位的功能,就叫做移位寄存器。
数码寄存器实质上就是一堆触发器“并联”,同时存进,同时读取,同时清零。
而移位寄存器实质上就是一堆触发器“串联”,依次存进,依次移位,依次读取。
举一个例子说明移位寄存器:
按照时钟周期,依次输入1、0、1、1,则寄存器的4位状态输出将依次是
1000
0100
1010
1101
这里可以看出移位寄存器的一个功能,即将串行输入转化为并行输出
利用移位寄存器可以构成移位寄存器型计数器
计数器的本质是循环,而如果我们把移位寄存器的首位相连,让数据从右边移出去又在左边移进来,就业能够构成循环,这样就成为了计数器。
环形计数器
比较直观的方式就是直接把输出引回输入,这样构成的计数器叫做环形计数器
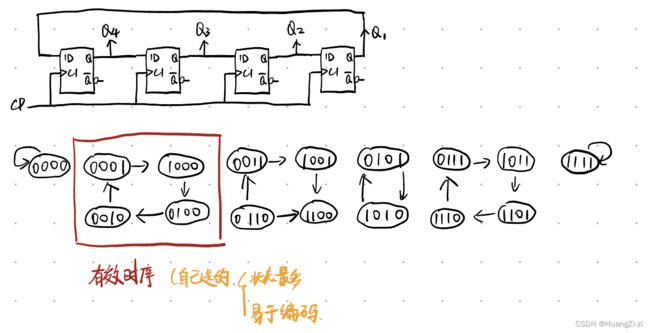
画状态转换图发现最大圈只有4个状态,但是同时有3个最大圈。这个时候就需要我们自己选择哪个是有效状态哪个是无效了。我们选择红色框里面的4个,因为只有1个1,方便编码译码。那其实选择后面只有1个0的,也差不多,这个选择是自由的。
自启动设计 \colorbox{black}{\color{white}自启动设计} 自启动设计
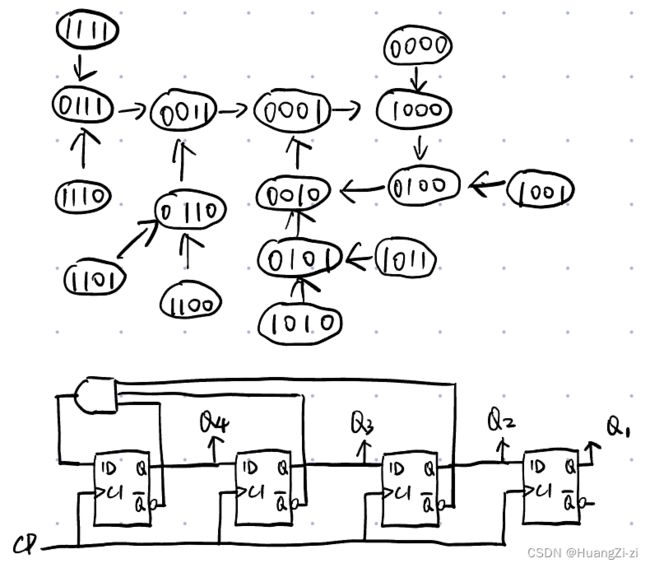
首先看原始电路的反馈,无论处于什么状态,返回的都是最尾一位(D4=Q1)。我们选择的有效时序是只有1个1,那么其他状态就都要向这些状态靠拢。如果状态里有多于1个1,那么我们返回0;没有1,,那么我们返回1;如果恰好一个1,返回最尾一位。

经过这样的反馈,所有其他状态最终都能回到只有一个1的有效状态中。
根据新的反馈再画状态转换图和电路图
扭环形计数器
对于扭环的理解,可以百度一下莫比乌斯带。应该就很好理解了。环形计数器返回的是最尾一位,而扭环形计数器返回的是最尾一位的非
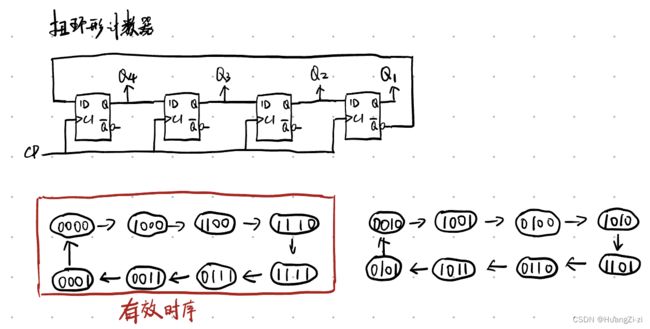
同样的从原始状态转化图,选取有效时序,然后想办法让无效时序中的一些变量转换到有效时序中去。
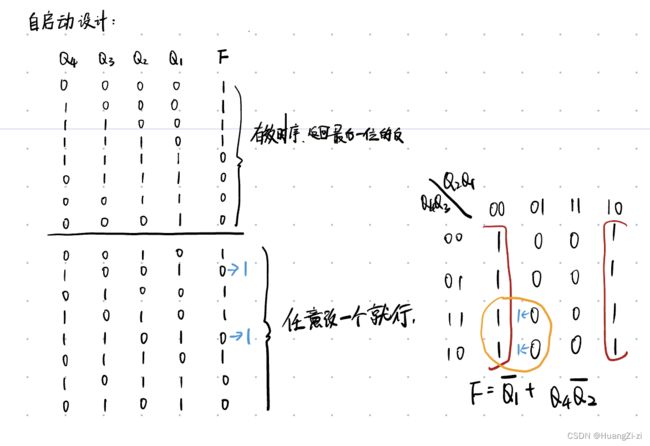
让无效时序的循环断开,转换进有效时序,理论上可以从任意一个状态下手。但是为了电路简便,我们还是画一下原始状态的卡诺图。在无效状态对应的0里面,任意选择一个改成1,就能打断无效循环,不过依然是为了电路简便,我们选择了图中标蓝的两个。于是就有了新的反馈方程。
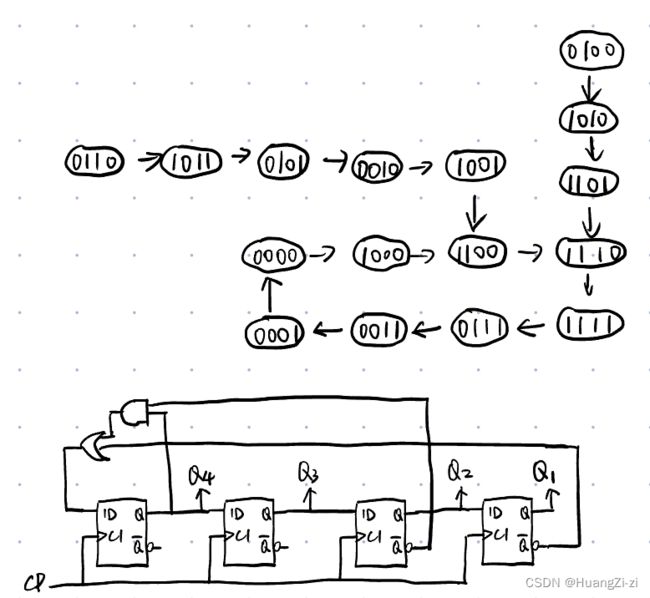
⋆ n 位 环 形 计 数 器 容 量 为 n \color{red}{\star{n位环形计数器容量为n}} ⋆n位环形计数器容量为n
⋆ n 位 扭 环 形 计 数 器 容 量 为 2 n \color{red}{\star{n位扭环形计数器容量为2n}} ⋆n位扭环形计数器容量为2n