【一起来刷题】基础排序问题之堆排序算法---手把手一步步图示剖析讲解,非常详细!一目了然,通俗易懂!
本章收录于专栏:一起来刷题,持续更新中……
更多精彩文章,欢迎大家关注我,一起学习,一起进步~
推荐专栏:大道至简之机器学习算法系列
目录
1、heapInsert
2、heapify
3、python代码实现
堆排序是基础排序问题中要介绍的最后一个十分重要的排序算法。在学习堆排序算法之前,需要明确几个基本概念:完全二叉树、大根堆,以及3个公式(见下文)。
完全二叉树:
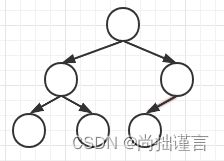
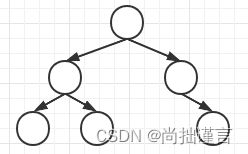
完全二叉树是在一棵树中,每一层并列的节点排列顺序必须是从左往右不留空的排列,如下图,左边是完全二叉树,右边不是:
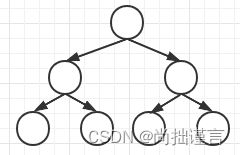
【拓展】如果每一层节点都排满了,那么它就是一个满二叉树:
所以,满二叉树是一种特殊的完全二叉树。
大根堆:
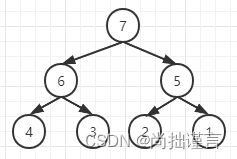
在一棵完全二叉树中,以任意节点为头结点的树中,头结点的值最大,称为大根堆。如下图:
不管是节点7还是6还是5,以其为头结点组成的树中,最大值都是它本身。
好了,有了上述概念,我们需要来看一下如何将数组和树结构进行转换。在实际工程中,树结构其实是一种脑补结构,它的实际存储结构仍然是一个数组。例如上图中,我们从上到下,从左往右依次将节点一字排开,就得到如下数组:
[7, 6, 5, 4, 3, 2, 1]
现在我们取数组中任意节点,比如【4】,它在数组中的索引为3,则4的父节点的索引就为:
如果该公式计算出的值为小数,需要向下取整,如0.5应取0。
它的左子节点的索引为:
![]()
它的右子节点的索引为:
![]()
请牢记上面三个公式!根据上述公式,也可以将一个数组还原成脑补树结构,。
现在我们有了上面介绍的这些基础知识后,就可以理解堆排序算法的原理了。总的来说,堆排序算法分为两个大步骤:自底向上建立大根堆的过程,我们称为heapInsert;自顶向下调整大根堆的过程,我们称为heapify。下面我们来一一介绍。
1、heapInsert
假如现在有一个空数组,你手头有一堆数,现在你要随机依次将手头的数一个一个丢进空数组中,最终要求数组里的数经过树还原后,是一个大根堆,怎么做?
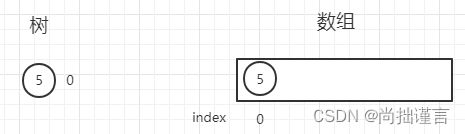
第一步:你丢出来的数为【5】,因为只有一个数,它自己就是个大根堆,所以放在空数组的0位置,那么树和数组长这样:
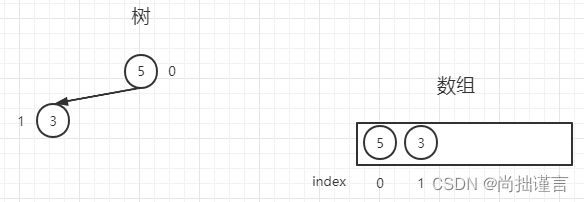
第二步:你丢出来的数为【3】,它将挂在【5】的左边,根据公式(index-1)/ 2 ,计算出【3】的父节点位置为(1-1)/ 2=0,即【3】要和0位置上的数【5】比较:【3】<【5】。我们发现【5】和【3】组成的树仍然是大根堆,所以【3】继续放在索引1的位置:
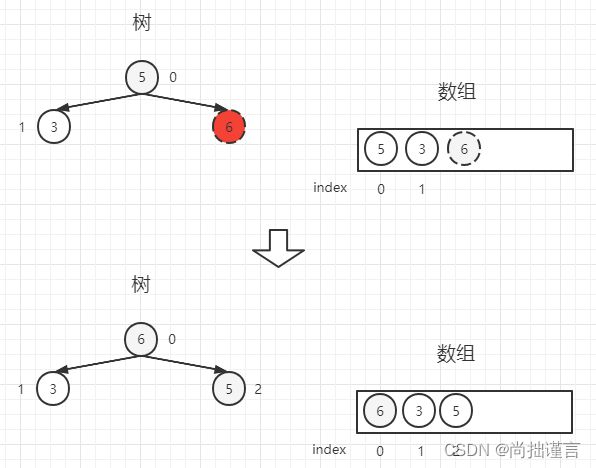
第三步:你丢出来的数为【6】,它将挂在【5】的右边,数组中的位置为2,从树上看,此时的树以【5】为头结点,其右子节点【6】大于父节点(2-1)/ 2=0 位置上的数【5】,不满足大根堆的条件,所以,【5】和【6】需要调整位置:
综上所述:每丢进来一个数,我们就根据父节点公式 (index-1)/2 来寻找这个数的父节点,并和父节点比较,如果它比父节点大,则和父节点交换位置。如果这个数的父节点也存在父节点,那么交换位置后,继续寻找父节点并对比。比如第四步:
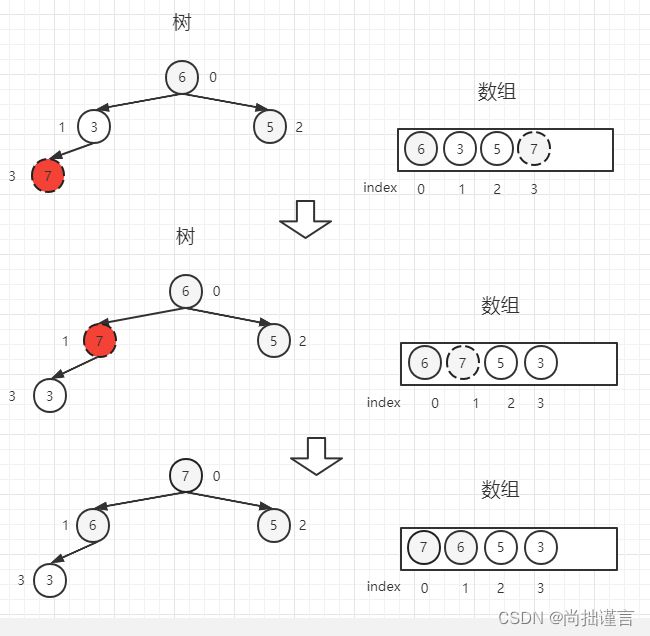
此时你丢进来的数为【7】,它将挂在【3】的左边,数组中位置为3,按照上述逻辑,【7】比父节点(3-1)/ 2=1位置上的数【3】大,【7】和【3】交换位置,交换完后,此时【7】的位置为1,发现【7】还有父节点(1-1)/ 2=0位置上的数【6】,且经过对比,【7】又比其父节点【6】大,所以继续交换:
根据上述步骤,我们依次往空数组中丢进了【5】、【3】、【6】、【7】四个数,并经过我们的调整,最终生成了大根堆,对应的数组为 [7, 6, 5, 3]。这就是heapInsert的过程,它是个自底向上建立大根堆的过程。代码实现上,如下所示:
def heapInsert(arr, index):
"""
自底向上,根据数组一次性构建大根堆
"""
father = (index - 1) // 2
while index > 0 and arr[index] > arr[father]:
arr[index], arr[father] = arr[father], arr[index]
index = father
father = (index - 1) // 22、heapify
假设现在你有了新的需求:你想提供一些数,把这些数丢进一个魔法空数组中,魔法空数组不仅要将这些数调整为大根堆,还要告诉你这个堆里最大的数是多少,并把这个最大的数取出来,堆里剩下的数仍然是个大根堆。
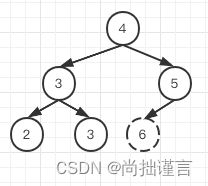
对于把一个数组调整为大根堆,用我们上面提到的heapInsert方法就可以,对于要知道堆里最大的数,只需要取大根堆的堆顶即可,也就是数组的第一个数,对于取出最大数,剩下的数再调整为大根堆,我们只需要再用一次heapInsert即可。如果我们将上述过程重复,并把每次取出的数用一个新的数组依次存放,那最终新的数组不就是个降序数组嘛,这貌似就实现了堆排序。但是这种实现方法至少存在两个明显的问题,第一个是这种堆排序方法需要额外开辟一个数组,如果是这样,那我们根本没必要再故弄玄虚搞一个堆排序这样的排序算法呀,每一次找到一个最小值放在新数组,不断重复不就可以了,另一个问题是,如果每一次都需要重建一棵树,时间复杂度无疑增大了不少。那我们怎么办呢?其实,可以在每一次取得到的堆顶之后,将它和最后一个节点交换位置,然后在脑补树结构中将该节点抹去就行了,这样就不需要开辟一个新数组了。而对于调整剩下的树成为大根堆,我们就不能使用自底向上的heapInsert方法了,为什么呢?看下图:
我们把【6】抹去,尾节点【4】调到堆顶, 我们如果自底向上调整,那本来底部一开始就满足大根堆的条件,就不会继续往上调整了,除非又回到我们刚才说的重建树,当然,我们也可以继续往上判断,直到判断到堆顶,但是到堆顶发现不满足大根堆,自底向上的heapInsert方法就不灵啦。所以,索性我们就直接从堆顶开始,向下调整,这个过程,就是heapify。对于脑补结构中的“抹去”该怎么操作呢?其实只需要用一个变量`size`记录当前树的节点数即可,每抹去一个节点,size减去1,在自顶向下的调整中,我们停止调整的条件就是调整的节点位置到达size值,在数组中就是到达数组的尾部。我们还是拿上图举例:
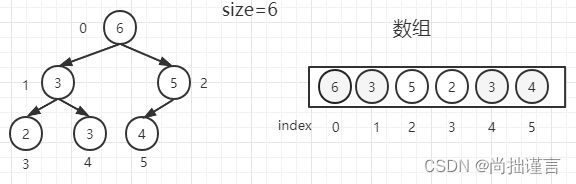
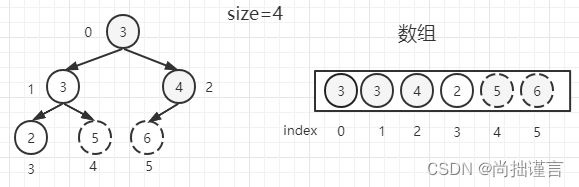
(1)假设我们经过heapInsert之后,得到了一个大根堆,此时原始size=6,然后将堆顶和堆尾互换位置,并抹去,别忘了size减去1,就得到下图(虚线表示该节点已经抹去):
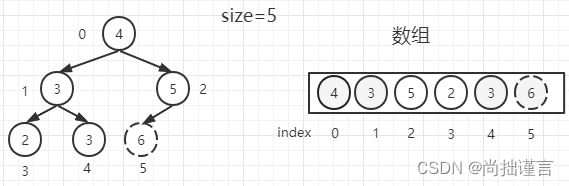
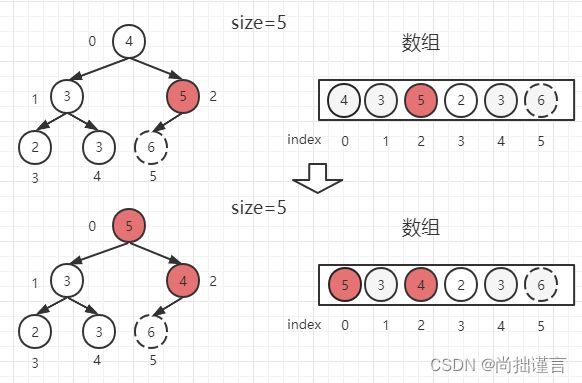
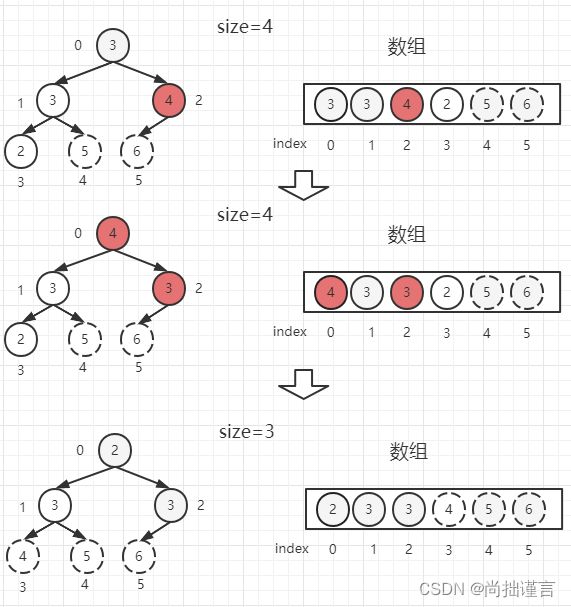
(2)从0位置父节点开始,根据公式(0*2)+ 1=1找到位置为1的左子节点【3】和(0*2)+ 2=2找到位置为2的右子节点【5】,谁大取谁,这里我们取【5】,并把大的那个数和父节点【4】对比,如果大于父节点,则交换位置,这里【5】和【4】交换位置,并把【4】作为当前父节点;否则,结束调整,因为整棵树只有父节点及其以上位置发生了变化,以下部分还是原来的大根堆结构,不用调整;
(3)以位置2的【4】为父节点,根据公式(2*2)+ 1=5找到位置为5的左子节点,发现5=size,停止调整。整棵树又是大根堆了,我们取堆顶【5】和位置4的堆尾【3】交换位置,并把堆尾抹去,别忘了size减去1:
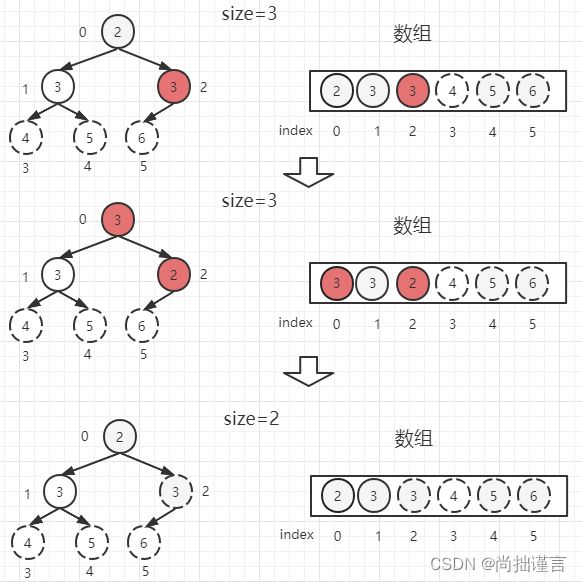
(4)从0位置父节点开始,根据公式(0*2)+ 1=1找到位置为1的左子节点【3】和(0*2)+ 2=2找到位置为2的右子节点【4】,谁大取谁,这里我们取【4】,并把大的那个数和父节点【3】对比,如果大于父节点,则交换位置,这里【4】和【3】交换位置,并把【3】作为当前父节点。以位置2的【3】为父节点,根据公式(2*2)+ 1=5找到位置为5的左子节点,发现5>size,停止调整。整棵树又是大根堆了,我们取堆顶【4】和位置3的堆尾【2】交换位置,并把堆尾抹去,别忘了size减去1:
(5)从0位置父节点开始,根据公式(0*2)+ 1=1找到位置为1的左子节点【3】和(0*2)+ 2=2找到位置为2的右子节点【3】,谁大取谁,由于这里左右孩子相等,这里我们先取右子节点【3】,并把【3】和父节点【2】对比,大于父节点,交换位置,并把【2】作为当前父节点。以位置2的【2】为父节点,根据公式(2*2)+ 1=5找到位置为5的左子节点,发现5>size,停止调整。整棵树又是大根堆了,我们取堆顶【3】和位置2的堆尾【2】交换位置,并把堆尾抹去,别忘了size减去1:
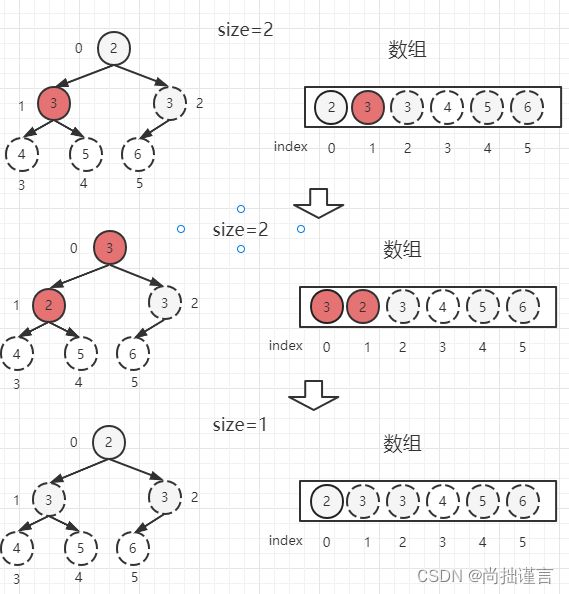
(6)从0位置父节点开始,根据公式(0*2)+ 1=1找到位置为1的左子节点【3】,由于这里已经没有右子节点了,这里我们直接取左子节点【3】,并把【3】和父节点【2】对比,大于父节点,交换位置,并把【2】作为当前父节点。以位置2的【2】为父节点,根据公式(1*2)+ 1=3大于>size,停止调整。整棵树又是大根堆了,我们取堆顶【3】和位置2的堆尾【2】交换位置,并把堆尾抹去,别忘了size减去1:
(7)现在整棵树只剩下一个【2】了,自己和自己再交换一下位置,size减去1,size=0,停止整个heapify过程,调整后的数组,就是个升序数组:
完成整个堆排序过程。代码实现上:
def heapify(arr, index, size):
"""
自顶向下,不断将当前数组重新调整为大根堆
"""
left = index * 2 + 1
right = left + 1
largestIndex = 0
# 错点: index < size
while left < size:
# 卡点
if right < size and arr[left] < arr[right]:
largestIndex = right
else:
largestIndex = left
largestIndex = largestIndex if arr[largestIndex] > arr[index] else index
if largestIndex == index:
break
arr[index], arr[largestIndex] = arr[largestIndex], arr[index]
index = largestIndex
left = index * 2 + 1
right = left + 1由于堆排序整个过程没有用到额外空间,所以堆排序的空间复杂度为O(1),而堆排序每次调整要么走树的左边要么走树的右边,所以着整个堆排序过程的时间复杂度为O(NlogN)。
综合时间复杂度和空间复杂度,堆排序可以算是最重要的一种基础排序算法,太牛了有木有~
3、python代码实现
from typing import List
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
if len(nums) == 1:
return nums
return self.heapSort(nums)
# 堆排序
def heapSort(self, nums):
if len(nums) == 1:
return nums
def heapInsert(arr, index):
"""
自底向上,根据数组一次性构建大根堆
"""
father = (index - 1) // 2
while index > 0 and arr[index] > arr[father]:
arr[index], arr[father] = arr[father], arr[index]
index = father
father = (index - 1) // 2
def heapify(arr, index, size):
"""
自顶向下,不断将当前数组重新调整为大根堆
"""
left = index * 2 + 1
right = left + 1
largestIndex = 0
# 错点: index < size
while left < size:
# 卡点
if right < size and arr[left] < arr[right]:
largestIndex = right
else:
largestIndex = left
largestIndex = largestIndex if arr[largestIndex] > arr[index] else index
if largestIndex == index:
break
arr[index], arr[largestIndex] = arr[largestIndex], arr[index]
index = largestIndex
left = index * 2 + 1
right = left + 1
def sort(arr):
"""
根据heapInsert和heapify排序数组
"""
for i in range(len(arr)):
heapInsert(arr, i)
size = len(arr)
arr[0], arr[size - 1] = arr[size - 1], arr[0]
size -= 1
while size > 0:
heapify(arr, 0, size)
arr[0], arr[size - 1] = arr[size - 1], arr[0]
size -= 1
return arr
return sort(nums)