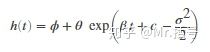三岁看大,七岁看老——基于退化模型进行剩余有效寿命预测的案例讲解
本篇是寿命预测系列的第二个案例,在看这篇之前可以先看一下这里。
使用退化模型进行机电产品剩余寿命预测在工程应用中比较常见,退化模型法又有着几种不同的具体形式,博主见到比较多的包括基于随机过程的退化模型、基于时间序列方法的退化模型以及基于线性/指数形式的退化模型。其中线性/指数模型最为简单,在MATLAB的相关文档[1]中也是以该类型模型作为例子的,所以本篇将对此模型的案例进行介绍。
额外提一句,基于时间序列的方法主要包括神经网络的方法(LSTM用的比较多)和ARIMA的方法。这两个方法在之前的博文中有所提及:
Mr.括号:用深度学习做了下中国股市预测,结果是...
Mr.括号:使用ARMA做时间序列预测全流程(附MATLAB代码)
随机过程方法以后有机会的话再写吧。
好了,现在开始。
1.案例描述
数据集是由Annual Conference of the Prognostics and Health Management Society[2]提供的公开数据集,从由20齿的小齿轮驱动的2MW的风力涡轮机高速轴收集。
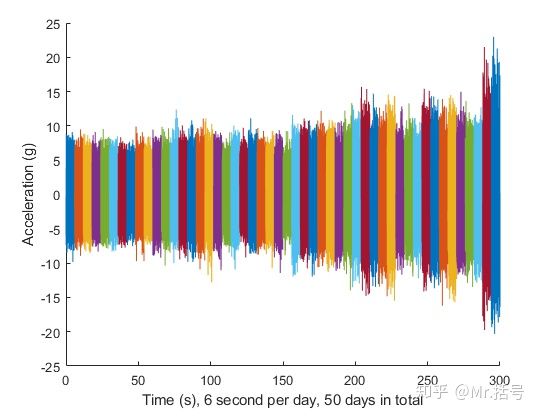
连续50天每天采集6秒振动信号,在50天时间里,一个内圈发生故障并导致轴承故障。
下图为这总共300秒振动数据的可视化结果,其中每个颜色段代表了一天的数据。
2.数据分析
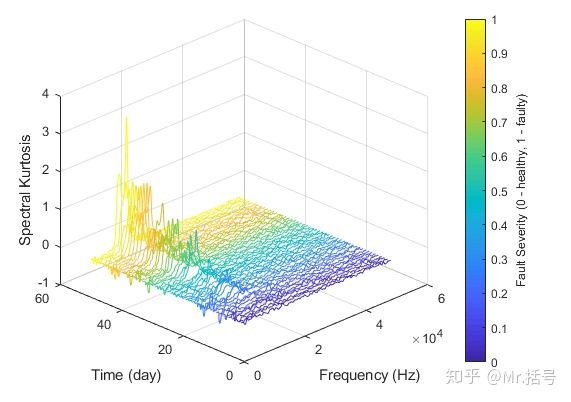
绘制原始数据的谱峭度(spectral kurtosis),并对数据进行分析。谱峭度的物理含义是能够描述信号在频率f处偏离高斯的程度,偏离高斯越大,谱峭度的值就越大。该特征值对信号中的瞬态成分十分敏感。
绘制谱峭度随时间和频率的变化如下图。
从图中可以看出,大约在10kHz处谱峭度处于峰值,且随着时间的推移逐渐增大。谱峭度的统计特征,如平均值、标准差等将是描述退化的潜在指标[3]。
3.特征提取
特征提取是建立退化模型前关键的一步,通常在特征提取之前,还会对数据进行一些预处理工作,比如模态分析、滤波等,由于该例子中原始数据类型简单、退化特征较为明显,所以没有进行这些工作。
所谓特征提取,就是用某种量化的特征值对目标信号的退化特征进行表征,通常会使用一些时域参数来表示。常用的时域参数在之前的文章中有所介绍:
Mr.括号:时域分析——有量纲特征值含义一网打尽
Mr.括号:时域分析——无量纲特征值含义一网打尽
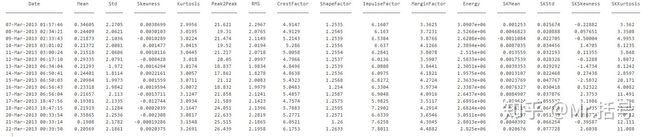
在该案例中,使用到的特征包括原始信号的:"Mean"; "Std"; "Skewness"; "Kurtosis"; "Peak2Peak","RMS"; "CrestFactor"; "ShapeFactor"; "ImpulseFactor"; "MarginFactor"; "Energy"。
以及谱峭度的:"Mean"; "Std"; "Skewness"; "Kurtosis"。
共计15中特征值,分别对每天的数据求取这15中特征值,可以得到一张大小为50*15的特征表。表格中的部分数据如下:
4.特征值后处理
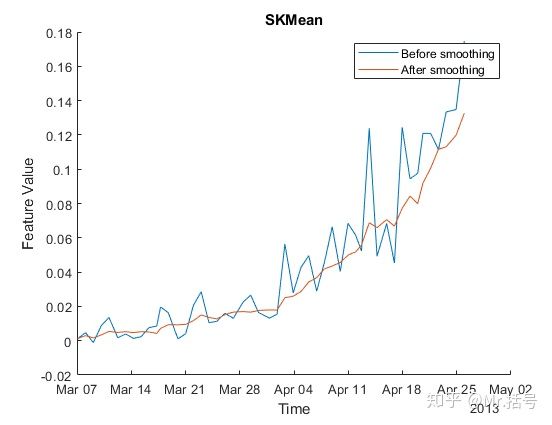
如前所述,该案例中没有进行预处理操作,不过在这里加入了后处理以削减噪声等干扰的影响。在特征值后处理中采用了滑动平均滤波器对退化数据进行平滑处理。下图为某特征值(谱峭度的均值)在使用滤波前后的对比图。需要注意的是,滑动平均会一定程度上引入信号延迟。
5.选定训练集
选取前20天的数据(生命周期的前40%)作为训练集。在进行特征值重要性排序和融合时使用的是训练集数据。
6.特征值重要性排序
对于选取的15组特征值,其表征退化的能力是不同的,我们需要对表征能力强的特征值进行筛选。
在这里,我们选择单调性作为量化指标:
式中,n为测量点数目,在本案例中n=50。m是对象产品个数,在本例中m=1。 是在第i个产品上的第j个特征值。diff()为求差分。
经过量化后,排序靠前的特征值如下图所示:
可见峭度的效果最好。我们选取单调性值大于0.3的5种特征值用于下一步的特征融合。
7.降维和特征融合
使用主成分分析(PCA)的方法进行降维和特征融合。不过在进行主成分分析之前,需要对特征值矩阵进行归一化。对于PCA如果不太了解的话可以看这篇:司南牧:5分钟理解PCA主成分分析。
将前两个主成分数据(PCA1、PCA2)进行可视化:
注意右侧colorbar中不同颜色代表的是天数,对比PCA1和PCA2,发现PCA1的值随时间变化的单调性更强。即更能表征“随着机器接近故障,成分值增加”的特点。
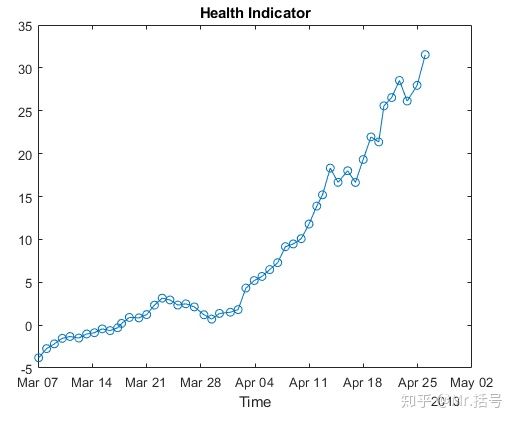
因而选取PCA1作为融合后的特征值,并称之为健康指标,用以表征对象的退化特征。由该指标表征的对象产品的退化过程如下图。
8.建立退化模型并计算RUL
无论是使用随机过程或者时间序列或者线性/指数模型方法,之前的7个步骤都是通用的。从这步开始才正式引入退化模型。
本案例中使用的是指数退化模型:
其中h(t)为健康指标,ϕ为常数项,θ和β为决定模型斜率的随机参数,其中θ为对数正态分布,β为高斯分布。
在进行RUL计算时,选取了第50天的健康指标作为失效阈值。
RUL迭代计算的步骤如下:
(1)使用已知退化数据(从1天开始)对指数退化模型参数进行估计。
(2)带入模型参数得到指数模型及其置信区间。
(3)依据失效阈值计算RUL。
(4)更新已知退化数据(从1天更新至49天),重复(1)~(4)。
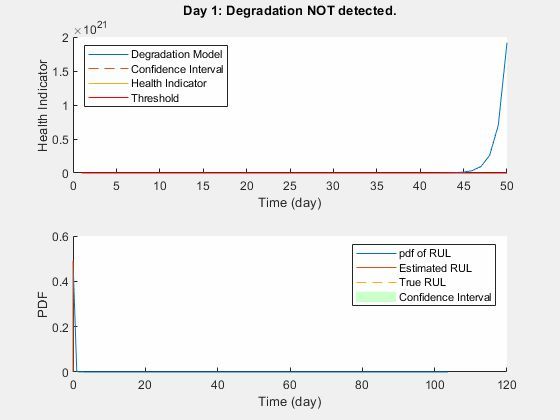
该迭代的动态过程可以参看下图,注意看小图中的图例。
9.性能分析
用下述两张图对指数退化模型计算RUL的性能进行描述:
上图中,蓝线为真实RUL值,红线为RUL预测值,蓝色阴影区域为真实RUL的±20%边界范围,红色阴影区域为RUL预测值的置信区间。
上图为RUL预测值在20%界限内的概率。也就是说当预测区间为真实RUL±20%范围内时,预测准确的概率值。
通过上述两张性能分析图,可以看出在预测集中(即20天以上的部分),随着更多的数据点用于拟合,预测将变得更加准确。
不过话说回来,这个使用指数退化模型的预测效果,只能说是差强人意。有兴趣的同学可以将第8步中的模型换成其他类型(比如时间序列方法),看看预测效果会不会更好一些。
结语
本篇是机电产品剩余有效寿命预测的第二篇,为了阅读的流畅性,本篇没有像上一篇那样贴关键代码。一方面是因为代码逻辑比较简单,另外一方面是数据处理量比较大,直到这篇文写完程序都还没有跑完,所以代码就不往上贴了。有兴趣要源码和数据集的同学可以关注我的公众号“看海的城堡”,微信号为“khscience”,回复“退化模型”就能拿到啦,公众号里可能还会有更多有趣的东西分享。
[1]Wind Turbine High-Speed Bearing Prognosis
[2]Acoustics and Vibration Database
[3]Saidi, Lotfi, et al. "Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR."Applied Acoustics120 (2017): 1-8.