攻克 Transformer && 评分函数（加性注意力、缩放点积注意力）

上篇博客链接直达：攻克 Transformer & 注意力机制的查询、键和值 & 有无参数的Nadaraya-Watson核回归

选择不同的注意⼒评分函数 a 会导致不同的注意⼒汇聚操作。在本文章中，我们将介绍两个流⾏的评分函数，稍后将⽤他们来实现更复杂的注意⼒机制。

目录

（1）评分函数概念

（2）加性注意力

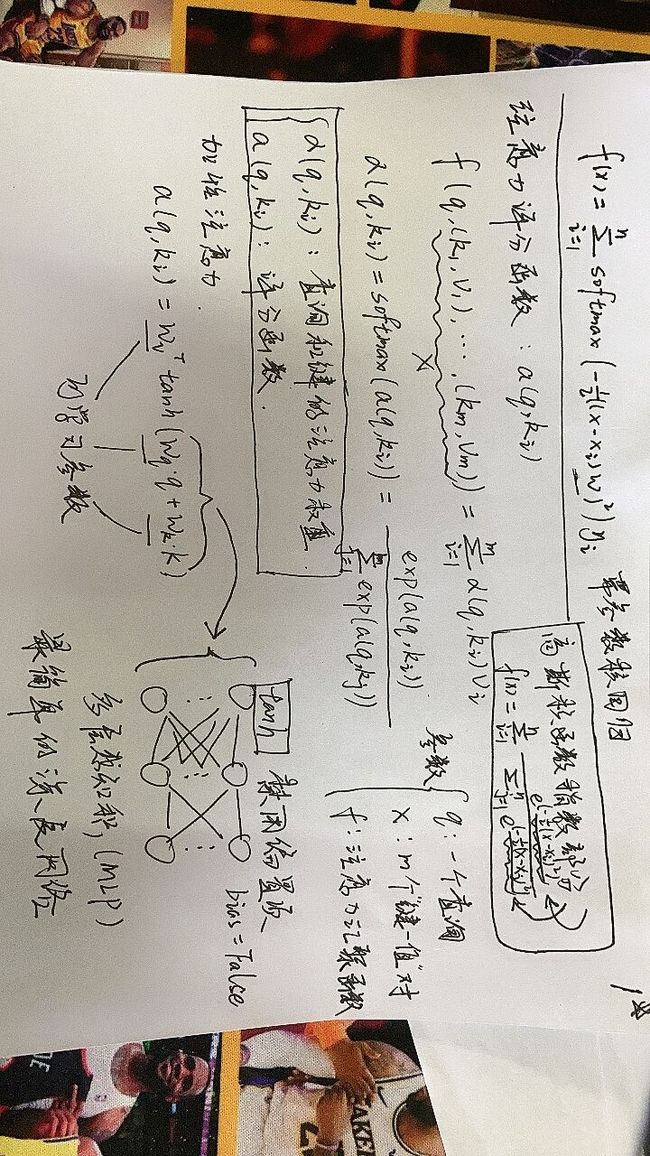
a) 公式

b) 草稿理解  

 c) 完整代码

 （3）缩放点积注意力

a) 公式

 b) 草稿理解

 c）完整代码

（4）掩蔽softmax操作

（5）总结

---

（1）评分函数概念

上一篇博客，我们使⽤⾼斯核来对查询和键之间的关系建模。

我们可以将高斯核指数部分视为注意⼒评分函数（attention scoring function），简称评分函数（scoring function），然后把这个函数的输出结果输⼊到 softmax 函数中进⾏运算。通过上述步骤，我们将得到与键对应的值的概率分布（即注意力权重）。 最后，注意⼒汇聚的输出就是基于这些注意⼒权重的值的加权和。

从宏观来看，我们可以使⽤上述算法来实现图1 中的注意⼒机制框架。图1 说明了如何将注意⼒汇聚 的输出计算成为值的加权和，其中 a 表示注意力评分函数。由于注意⼒权重是概率分布，因此加权和其本质上是加权平均值。

图1 计算注意力汇聚的输出为值的加权和 

评分函数公式：

（2）加性注意力

a) 公式

b) 草稿理解  

注意：h是隐藏单元数

 c) 完整代码

建议：自己调试，观看各个阶段的 Q, K, V 张量的尺寸大小的变化。

import matplotlib.pyplot as plt
import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)


# 指定每个矩阵的有效长度
out_mask_1 = masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))
# 使用二维张量，为矩阵样本中的每一行指定有效长度。
out_mask_2 = masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
print("*************************mask_softmax*********************")
print(out_mask_1)
print(out_mask_2)


# 2、20、8、0.1
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)  # [2, 8]
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)  # [20, 8]
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)  # [8, 1]
        self.dropout = nn.Dropout(dropout)  # 0.1 # 随机将10%的元素置为0

    # torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2)), torch.Size([2, 10, 4]), torch.tensor([2, 6])
    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)  # [2, 1, 8], [2, 10, 8]

        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)

        # print(queries.unsqueeze(2), keys.unsqueeze(1))  # [2, 1, 1, 8], [2, 1, 10, 8]
        # print(features)  # [2, 1, 10, 8]
        features = torch.tanh(features)

        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)  # [2, 1, 10, 8]*[8, 1]=[2, 1, 10, 1]>>>[2, 1, 10]

        # 第一个矩阵的每一行保留有效长度为2
        # 第二个矩阵的每一行保留有效长度为6
        self.attention_weights = masked_softmax(scores, valid_lens)  # [2, 1, 10]
        print("*************************self.attention_weights*********************")
        print(self.attention_weights)

        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        output = torch.bmm(self.dropout(self.attention_weights), values)  # [2, 1, 4]

        return output


queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)  # [2, 10, 4]

# 定义序列的有效长度
valid_lens = torch.tensor([2, 6])

attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8, dropout=0.1)
attention.eval()
print("*************************Q,K,V*********************")
print(queries.size(), keys.size(), values.size())
output = attention(queries, keys, values, valid_lens)
print("*************************output*********************")
print(output.size())
print(output)

# 显示注意力权重特征图
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')
plt.show()

 （3）缩放点积注意力

a) 公式

 b) 草稿理解

 c）完整代码

建议：自己调试，观看各个阶段的 Q, K, V 张量的尺寸大小的变化。

import math

import matplotlib.pyplot as plt
import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行 softmax 操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)


class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1, 2)) / math.sqrt(d)  # [2, 1, 10]
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)  # [2, 1, 4]


queries, keys = torch.normal(0, 1, (2, 1, 2)), torch.ones((2, 10, 2))
# print(keys.transpose(1, 2))  # 转置 [2, 2, 10]

# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)  # [2, 10, 4]
valid_lens = torch.tensor([2, 6])

attention = DotProductAttention(dropout=0.5)
attention.eval()
output = attention(queries, keys, values, valid_lens)
print("*************************output*********************")
print(output.size())
print(output)

# 显示注意力权重特征图
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')
plt.show()

（4）掩蔽softmax操作

softmax操作⽤于输出⼀个概率分布作为注意⼒权重。在某些情况下，并⾮所有的值都应该被纳⼊到注意⼒汇聚中。某些⽂本序列被填充了没有意义的特殊词元，为了仅将有意义的词元作为值来获取注意⼒汇聚，我们可以指定⼀个有效序列⻓度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。通过这种⽅式，我们可以在下⾯的 masked_softmax 函数中实现这样的掩蔽softmax操作（masked softmax operation），其中任何超出有效⻓度的位置都被掩蔽置为0。

import matplotlib.pyplot as plt
import torch
from torch import nn
from d2l import torch as d2l


def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)


# 指定每个矩阵的有效长度
out_mask_1 = masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))
# 使用二维张量，为矩阵样本中的每一行指定有效长度。
out_mask_2 = masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))
print("*************************mask_softmax*********************")
print(out_mask_1)
print(out_mask_2)

 >>>output

*************************mask_softmax*********************

tensor([[[0.5607, 0.4393, 0.0000, 0.0000],  # L=2
             [0.6431, 0.3569, 0.0000, 0.0000]],  # L=2

            [[0.4818, 0.2435, 0.2747, 0.0000],  # L=3
             [0.2330, 0.2912, 0.4758, 0.0000]]])  #L=3

tensor([[[1.0000, 0.0000, 0.0000, 0.0000],  # L=1
             [0.3486, 0.4044, 0.2470, 0.0000]],  # L=3

            [[0.6019, 0.3981, 0.0000, 0.0000],  # L=2
             [0.2037, 0.1969, 0.2232, 0.3763]]])  # L=4

可以指定矩阵的有效长度，也可以指定每一行的有效长度

（5）总结

• 将注意⼒汇聚的输出计算可以作为值的加权平均，选择不同的注意⼒评分函数会带来不同的注意⼒汇聚操作。 
• 当查询和键是不同长度的⽮量时，可以使⽤可加性注意⼒评分函数。当它们的长度相同时，使⽤缩放的 “点－积”注意⼒评分函数的计算效率更⾼。

未完待续。。。

>>>如有疑问，欢迎评论区一起探讨