GAT-图注意力模型

GAT简介

什么是GAT

GAT(Graph Attention Networks)，即图注意力神经网络，根据名称，我们可以知道这个网络肯定是和注意力架构绑定的，那么为什么需要注意力架构呢？
在直推式模型如GCN中，使用拉普拉斯矩阵来获取顶点特征，但是，拉普拉斯矩阵存在着一些问题，在运算的时候，需要把整个图所有节点都放进模型中，这就导致无法预测新节点。而GAT采用Attention架构，只负责将该节点的邻居节点进行计算，也就是只计算子图的一部分，这样，就可以避免全图计算。

注意力机制

假设，图中有N个节点，每个节点都有F维特征，可以表示为如下：
$h=\{h_1,h_2,...h_N\},h_i\in R^F$
为了能够保留足够的表达能力，将输入特征转为高阶特征，需要进行至少一次的线性变换，如对节点i,j进行如下转换：
$e_{ij}=a(W{h}_i,W{h}_j)$
其中，W是随机权重矩阵，$e_{ij}$是节点i对节点j的影响力系数。

如何计算节点i，j之间的相关度呢？论文中采用了一个单层的前馈神经网络，采用LeakyReLU作为非线性激活函数，公式如下：
$e_{ij}=LeakyReLU(a^T[W{h}_i||W{h}_j])$
其中，||表示拼接操作。

在计算节点之间的注意力系数时，往往可能会计算所有节点之间的系数，如果这样计算的话，就需要加载所有的图节点，和实际的目的不符。实际上，论文使用了masked attention，只需要计算当前节点和其邻居节点的系数即可。

为了更好的在不同节点之间分配权重，我们将目标节点与所有邻居节点计算出来的系数进行归一化处理，公式如下：
${\alpha }_{ij}=softma{x}_j(e_{ij})=\frac{exp(e_{ij})}{{\sum }_{k\in N_i}exp(e_{ik})}$
其中，k是节点i的邻居节点。

完整的权重系数计算公式为：
${\alpha }_{ij}=softma{x}_k(e_{ij})=\frac{exp(LeakyReLU(a^T[W{h}_i||W{h}_j]))}{{\sum }_{k\in N_i}exp(LeakyReLU(a^T[W{h}_i||W{h}_j]))}$

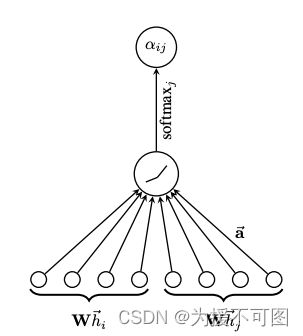
得到整体的归一化系数后，与节点对应的特征进行组合，经过非线性激活函数后，每个节点最终输出的特征向量如下所示：
${h_i}^{\prime }=\sigma (\sum _{j\in N_i}{\alpha }_{ij}W{h}_j)$

以上，就是如何计算每个节点和节点之间的注意力系数了。

多头注意力

论文中采用了多头注意力，图中显示有三条有颜色的线，对应本文中选取的K=3，即3个注意力机制，节点1和节点2-6分别计算各自的注意力系数，最终，将所有的系数矩阵进行拼接然后求平均操作，公式如下：
${h_i}^{\prime }=\sigma (\frac{1}{K}\sum _{k=1}^K\sum _{j\in N_i}{\alpha }_{ij}^k{W}^k{h}_j)$
其中，${\alpha }_{ij}^k$是第k组注意力机制计算出的权重系数，$W^k$是对应的输入线性变换矩阵。

以上，就是GAT所有的理论知识点了。

代码

GAT模型

class GAT(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
        """Dense version of GAT."""
        super(GAT, self).__init__()
        self.dropout = dropout
        #第一层多头注意力机制
        self.attentions = [GraphAttentionLayer(nfeat,
                                               nhid,
                                               dropout=dropout,
                                               alpha=alpha,
                                               concat=True) for _ in range(nheads)]
        for i, attention in enumerate(self.attentions):
            self.add_module('attention_{}'.format(i), attention)
		#第二层多头注意力机制
        self.out_att = GraphAttentionLayer(nhid * nheads,
                                           nclass,
                                           dropout=dropout,
                                           alpha=alpha,
                                           concat=False)

    def forward(self, x, adj):
    	#对特征数据进行dropout
        x = F.dropout(x, self.dropout, training=self.training)
        #对8个注意力系数矩阵进行拼接，cat(2708*8)=2708*64
        x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
        #再次进行dropout操作
        x = F.dropout(x, self.dropout, training=self.training)
        #第二层注意力模型2708*64×64*7=2708*7并进行激活
        x = F.elu(self.out_att(x, adj))
        #对每行特征进行softmax，获取对应概率标签
        return F.log_softmax(x, dim=1)

1、执行模型，将输入的特征数据进行dropout=0.6；
2、第一层注意力为多头：遍历每个attentions，传进去的数据是特征矩阵x和邻接矩阵adj，然后对每个注意力矩阵进行拼接(调用方法GraphAttentionLayer(1433,8,0.6,0.2,8))；
3、再次对特征数据进行dropout=0.6；
4、第二层注意力为单个：通过一个激活函数elu之后，进行softmax输出标签概率。

Attention模型

class GraphAttentionLayer(nn.Module):
    """
    Simple GAT layer, similar to https://arxiv.org/abs/1710.10903
    """
    '''
    in_features:特征数-1433
    out_features:隐藏单元数-8
    dropout：0.6
    alpha：0.2
    '''
    def __init__(self, in_features, out_features, dropout, alpha, concat=True):
        super(GraphAttentionLayer, self).__init__()
        self.dropout = dropout
        self.in_features = in_features
        self.out_features = out_features
        self.alpha = alpha
        self.concat = concat
		#1433*8
        self.W = nn.Parameter(torch.empty(size=(in_features, out_features)))
        nn.init.xavier_uniform_(self.W.data, gain=1.414)
        #16*1
        self.a = nn.Parameter(torch.empty(size=(2*out_features, 1)))
        nn.init.xavier_uniform_(self.a.data, gain=1.414)

        self.leakyrelu = nn.LeakyReLU(self.alpha)

    def forward(self, h, adj):
    	#2708*1433×1433*8=2708*8
        Wh = torch.mm(h, self.W) # h.shape: (N, in_features), Wh.shape: (N, out_features)
        #2708*2708
        e = self._prepare_attentional_mechanism_input(Wh)
		#创建等大小的负无穷矩阵2708*2708
        zero_vec = -9e15*torch.ones_like(e)
        #将邻接矩阵为0的地方进行更新
        attention = torch.where(adj > 0, e, zero_vec)
        #对注意力系数矩阵归一化
        attention = F.softmax(attention, dim=1)
        #再随机进行dropout操作
        attention = F.dropout(attention, self.dropout, training=self.training)
        #获取注意力系数矩阵2708*2708×2708*8=2708*8
        h_prime = torch.matmul(attention, Wh)
        if self.concat:
        	#进行一次激活函数
            return F.elu(h_prime)
        else:
            return h_prime
	#Wh为线性矩阵
    def _prepare_attentional_mechanism_input(self, Wh):
        # Wh.shape (N, out_feature)
        # self.a.shape (2 * out_feature, 1)
        # Wh1&2.shape (N, 1)
        # e.shape (N, N)
        #2708*8×8*1=2708*1
        Wh1 = torch.matmul(Wh, self.a[:self.out_features, :])
        Wh2 = torch.matmul(Wh, self.a[self.out_features:, :])
        # broadcast add
        #2708*1+2708*1.T=2708*2708
        e = Wh1 + Wh2.T
        return self.leakyrelu(e)

    def __repr__(self):
        return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'

以上代码为模型在直推学习下进行，模型代码以及后期所做的注释已经标注在以上信息中，请大家自行观看。

模型使用

直推学习

1、两层GAT模型，第一层多头注意力，输出特征维度（共64个特征），激活函数为指数线性单元（ELU）；
2、第二层单头注意力，计算个特征（为分类数），接softmax激活函数；
3、为了处理小的训练集，模型中大量采用正则化方法，具体为L2正则化；
4、dropout；

归纳学习：

1、三层GAT模型，前两层多头注意力，输出特征维度（共1024个特征），激活函数为指数非线性单元（ELU）；
2、最后一层用于多标签分类，，每个头计算121个特征，后接logistic sigmoid激活函数；
3、不使用正则化和dropout；
4、使用了跨越中间注意力层的跳跃连接。

结语

以上就是小编对GAT模型的一个理解，大家如果要有纠正或者补充的话，请留言或者加QQ：1143948594，随时联系啦！！！
附：论文链接：GRAPH ATTENTION NETWORKS