散列表(线性、平方、双散列、分离链表解决冲突)

目录

前言

用线性探测法解决冲突

实现代码：

运行结果：

 用平方探测法解决冲突

实现代码：

运行结果：

 用双散列探测解决冲突

实现代码：

运行结果：

 用分离链接法解决冲突

实现代码：

运行结果：

 结语

---

前言

        相信看到这篇博客的小伙伴应该都是在学数据结构，博主也是正在学数据结构，最近挺忙的，所以就没时间自己想代码了，主要是抄了书上的模板，然后按自己的想法进行了一些修改，书上是只有平方探测法的，我简单的改了一下，分出了四种方法，如果有不对的地方欢迎大家指出。

        还需要说明的一点是，我这些代码其实是为了完成老师布置的数据结构作业而写的，所以还是有一些题目的。简单的贴一下代码就行了，不需要将解释太多，代码里都有注释。

用线性探测法解决冲突

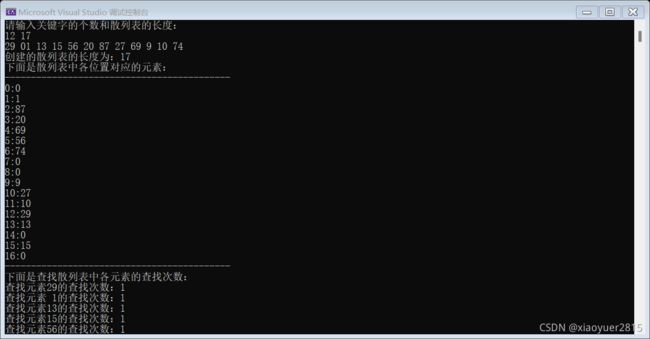
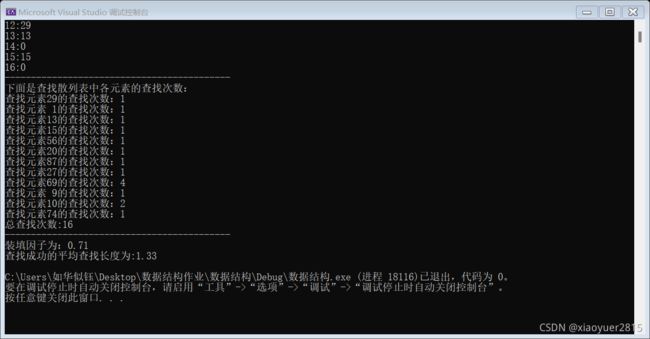
        设有一组关键字{29，01，13，15，56，20，87，27，69，9，10，74}，散列函数为H(key)=key%17,采用线性探测方法解决冲突，试在0到18的散列地址空间中对该关键字序列构造散列表，并计算成功查找的平均查找长度。

实现代码：

#include
#include
typedef int ElementType;//定义散列关键词类型
typedef enum { Legitimate, Empty, Deleted }EntryType;
//对应有合法元素、空单元、有已删除元素三种状态
typedef struct HashEntry {//散列表单元类型
	ElementType Data;//存放元素
	EntryType Info;//单元状态
}Cell;
//Cell 为结构体变量，不是结构体指针变量
typedef struct TblNode {//散列表结点定义
	int TableSize;//表的最大长度
	Cell* cells;//存放散列单元数据的数组
}*HashTable;
int Hash(ElementType key, int TableSize) {
	return key % TableSize;
}
HashTable CreateTable(int TableSize) {//创建散列表
	HashTable H = (HashTable)malloc(sizeof(struct TblNode));
	H->TableSize = TableSize;
	H->cells = (Cell*)malloc(H->TableSize * sizeof(Cell));//给散列表开辟空间
	for (int i = 0; i < H->TableSize; i++) {//将散列表全部标记为空
		H->cells[i].Info = Empty;
		H->cells[i].Data = 0;
	}
	return H;
}
int Find(HashTable H, ElementType key) {//在散列表中寻找key元素并返回该元素的地址
	int i = key % H->TableSize;
	while (H->cells[i].Data != key) {
		i++;
		if (H->cells[i].Info == Deleted || H->cells[i].Info == Empty)
			return -1;//没找到
	}
	return i;
}
int Find1(HashTable H, ElementType key) {//返回查找元素key的查找次数
	int i = key % H->TableSize, sum = 1;
	while (H->cells[i].Info == Legitimate) {
		if (H->cells[i].Data == key) return sum;
		else {
			sum++; i++;
		}
		if (i >= H->TableSize)i = 0;
	}
	return sum;
}
void Insert(HashTable H, ElementType key) {
	int i = key % H->TableSize;
	while (H->cells[i].Info == Legitimate) i++;
	H->cells[i].Data = key;//放入元素
	H->cells[i].Info = Legitimate;//修改状态
}
void Delete(HashTable H, ElementType key) {//在散列表中将元素key删除
	int i = Find(H, key);//在散列表中查找元素key
	if (i == -1)return;//元素key在散列表中不存在
	H->cells[i].Info = Deleted;//修改状态即可
}
int main() {
	int n, choice, lenth, a[1005] = { 0 };
	ElementType key;
	printf("请输入关键字的个数和散列表的长度：\n");
	scanf("%d %d", &n, &lenth);
	HashTable H = CreateTable(lenth);//创建散列表，定义大小为11
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i]);
		Insert(H, a[i]);
	}
	printf("创建的散列表的长度为：%d\n", H->TableSize);
	printf("下面是散列表中各位置对应的元素：\n");
	printf("-------------------------------------------\n");
	for (int i = 0; i < H->TableSize; i++) printf("%d:%d \n", i, H->cells[i].Data);
	printf("-------------------------------------------\n");
	printf("下面是查找散列表中各元素的查找次数：\n");
	double x = double(n) / double(H->TableSize), sum = 0;
	//计算成功查找的平均查找长度:
	for (int i = 0; i < n; i++) {
		sum += Find1(H, a[i]);
		printf("查找元素%2d的查找次数：%d\n", a[i], Find1(H, a[i]));
	}
	printf("总查找次数:%d\n", int(sum));
	printf("-------------------------------------------\n");
	double ASL = sum / double(n);
	printf("装填因子为：%.2lf\n", x);
	printf("查找成功的平均查找长度为:%.2lf\n", ASL);
	return 0;
}
/*
12 17
29 01 13 15 56 20 87 27 69 9 10 74
9 13
92 81 58 21 57 45 161 38 117
9 9
47 7 29 11 9 84 54 20 30
*/

运行结果：

 

 用平方探测法解决冲突

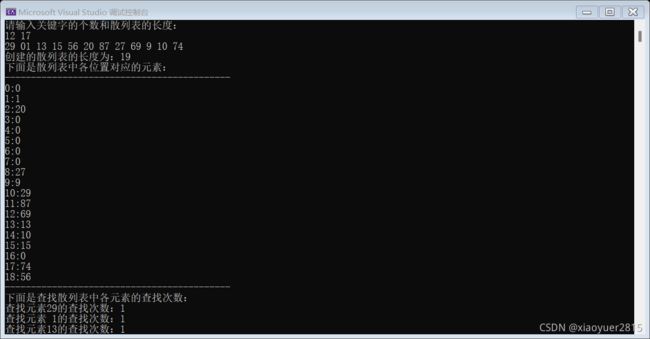
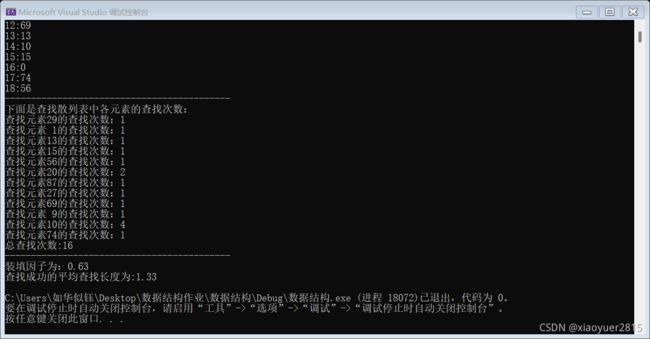
        设有一组关键字{29，01，13，15，56，20，87，27，69，9，10，74}，散列函数为H(key)=key%17,采用平方探测方法解决冲突，试在0到18的散列地址空间中对该关键字序列构造散列表。

实现代码：

#include
#include
#define MAXTABLESIZE 100000//允许开辟的最大散列表长度
typedef int ElementType;//定义散列关键词类型
typedef enum { Legitimate, Empty, Deleted }EntryType;
//对应有合法元素、空单元、有已删除元素三种状态
typedef struct HashEntry {//散列表单元类型
	ElementType Data;//存放元素
	EntryType Info;//单元状态
}Cell;
//Cell 为结构体变量，不是结构体指针变量
typedef struct TblNode {//散列表结点定义
	int TableSize;//表的最大长度
	Cell* cells;//存放散列单元数据的数组
}*HashTable;
int Hash(int key, int TableSize) {
	return key % TableSize;
}
bool primer(int n) {//判断素数的函数
	if (n < 2)return false;
	for (int i = 2; i * i <= n; i++)
		if (n % i == 0)return false;
	return true;
}
int NextPrime(int N) {//返回大于N且不超过MAXTABLESIZE的最小素数
	int i, p = (N % 2 != 0) ? N + 2 : N + 1;//将大于N的奇数的值赋给p
	while (p <= MAXTABLESIZE) {
		if (primer(p))break;
		else p += 2;//不是素数就判断下一个奇数
	}
	return p;
}
HashTable CreateTable(int TableSize) {//开放定址法的初始化函数
	HashTable H = (HashTable)malloc(sizeof(struct TblNode));
	H->TableSize = NextPrime(TableSize);
	H->cells = (Cell*)malloc(H->TableSize * sizeof(Cell));//给散列表开辟空间
	for (int i = 0; i < H->TableSize; i++) {//将散列表全部标记为空
		H->cells[i].Info = Empty;
		H->cells[i].Data = 0;
	}
	return H;
}
int Find(HashTable H, ElementType key) {//找到空位置
	int CurrentPos, NewPos, CNum = 0;
	NewPos = CurrentPos = Hash(key, H->TableSize);
	while (H->cells[NewPos].Info != Empty && H->cells[NewPos].Info != Deleted && H->cells[NewPos].Data != key) {//不为空且该位置存的元素元素不为key
		if (++CNum % 2) {//奇数次冲突
			NewPos = CurrentPos + (CNum + 1) * (CNum + 1) / 4;
			if (NewPos >= H->TableSize)NewPos = NewPos % H->TableSize;//保证NewPos不大于散列表的元素个数
		}
		else {//偶数次冲突
			NewPos = CurrentPos - CNum * CNum / 4;
			while (NewPos < 0) NewPos += H->TableSize;//保证NewPos大于0
		}
	}
	return NewPos;
}
int Find1(HashTable H, ElementType key) {//返回查找元素key的查找次数
	int i = key % H->TableSize, sum = 1, j = i;
	while (H->cells[i].Info == Legitimate) {
		if (H->cells[i].Data == key) return sum;
		else if (H->cells[i].Data != key) {
			if (sum % 2 != 0) {
				i = j + (sum + 1) * (sum + 1) / 4;
				if (i >= H->TableSize)i = i % H->TableSize;
			}
			else {
				i = j - sum * sum / 4;
				while (i < 0) i += H->TableSize;
			}
			sum++;
		}
	}
	return sum;
}
bool Insert(HashTable H, ElementType key) {
	int Pos = Find(H, key);
	if (H->cells[Pos].Info != Legitimate) {
		H->cells[Pos].Info = Legitimate;
		H->cells[Pos].Data = key;
		return true;
	}
	else {
		//printf("键值已存在\n");
		return false;
	}
}
void Delete(HashTable H, ElementType key) {//在散列表中将元素key删除
	int i = Find(H, key);//在散列表中查找元素key
	if (H->cells[i].Info == Legitimate) {
		H->cells[i].Info = Deleted;
	}
	else return;//没找到给元素直接退出
}

int main() {
	int n, choice, lenth, a[1005] = { 0 };
	ElementType key;
	printf("请输入关键字的个数和散列表的长度：\n");
	scanf("%d %d", &n, &lenth);
	HashTable H = CreateTable(lenth);//创建散列表，定义大小为11
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i]);
		Insert(H, a[i]);
	}
	printf("创建的散列表的长度为：%d\n", H->TableSize);
	printf("下面是散列表中各位置对应的元素：\n");
	printf("-------------------------------------------\n");
	for (int i = 0; i < H->TableSize; i++) printf("%d:%d \n", i, H->cells[i].Data);
	printf("-------------------------------------------\n");
	printf("下面是查找散列表中各元素的查找次数：\n");
	double x = double(n) / double(H->TableSize), sum = 0;
	//计算成功查找的平均查找长度:
	for (int i = 0; i < n; i++) {
		sum += Find1(H, a[i]);
		printf("查找元素%2d的查找次数：%d\n", a[i], Find1(H, a[i]));
	}
	printf("总查找次数:%d\n", int(sum));
	printf("-------------------------------------------\n");
	double ASL = sum / double(n);
	printf("装填因子为：%.2lf\n", x);
	printf("查找成功的平均查找长度为:%.2lf\n", ASL);
	return 0;
}
/*
12 17
29 01 13 15 56 20 87 27 69 9 10 74
9 13
92 81 58 21 57 45 161 38 117
9 9
47 7 29 11 9 84 54 20 30
*/

运行结果：

 

 用双散列探测解决冲突

        设有一组关键字{92，81，58，21，57，45，161，38，117}，散列函数h(key)=key%13,采用下列双散列探测方法解决第i次冲突：h(key)=(h(key)+i*h2(key))mod 13，其中h2(key)=(key mod 11 )+1。试在0到12的散列地址空间中对该关键字序列构造散列表。

实现代码：

#include
#include
#define MAXTABLESIZE 100000//允许开辟的最大散列表长度
typedef int ElementType;//定义散列关键词类型
typedef enum { Legitimate, Empty, Deleted }EntryType;
//对应有合法元素、空单元、有已删除元素三种状态
typedef struct HashEntry {//散列表单元类型
	ElementType Data;//存放元素
	EntryType Info;//单元状态
}Cell;
//Cell 为结构体变量，不是结构体指针变量
typedef struct TblNode {//散列表结点定义
	int TableSize;//表的最大长度
	Cell* cells;//存放散列单元数据的数组
}*HashTable;
int Hash(int key, int TableSize) {
	return key % TableSize;
}
int Hash2(int key, int TableSize) {
	return key % 11 + 1;
	//return TableSize - (key % TableSize);
}
bool primer(int n) {//判断素数的函数
	if (n < 2)return false;
	for (int i = 2; i * i <= n; i++)
		if (n % i == 0)return false;
	return true;
}
int NextPrime(int N) {//返回大于N且不超过MAXTABLESIZE的最小素数
	int i, p = (N % 2 != 0) ? N + 2 : N + 1;//将大于N的奇数的值赋给p
	while (p <= MAXTABLESIZE) {
		if (primer(p))break;
		else p += 2;//不是素数就判断下一个奇数
	}
	return p;
}
HashTable CreateTable(int TableSize) {//开放定址法的初始化函数
	HashTable H = (HashTable)malloc(sizeof(struct TblNode));
	//H->TableSize = NextPrime(TableSize);
	H->TableSize = TableSize;
	H->cells = (Cell*)malloc(H->TableSize * sizeof(Cell));//给散列表开辟空间
	for (int i = 0; i < H->TableSize; i++) {//将散列表全部标记为空
		H->cells[i].Info = Empty;//初始化状态
		H->cells[i].Data = 0;//初始化数据
	}
	return H;
}
int Find(HashTable H, ElementType key) {//找到空位置或被删除的位置
	int CurrentPos, NewPos, i = 0;
	NewPos = CurrentPos = Hash(key, H->TableSize);
	while (H->cells[NewPos].Info != Empty && H->cells[NewPos].Info != Deleted && H->cells[NewPos].Data != key) {//不为空且该位置存的元素元素不为key
		i++;
		NewPos = (CurrentPos + i * Hash2(key, H->TableSize)) % H->TableSize;
	}
	return NewPos;
}
int Find1(HashTable H, ElementType key) {//返回查找元素key的查找次数
	int i = key % H->TableSize, sum = 1, j = i;
	while (H->cells[i].Info == Legitimate) {
		if (H->cells[i].Data == key) return sum;
		else if (H->cells[i].Data != key) {
			i = (j + sum * Hash2(key, H->TableSize)) % H->TableSize;
			sum++;
		}
	}
	return sum;
}
bool Insert(HashTable H, ElementType key) {
	int Pos = Find(H, key);
	if (H->cells[Pos].Info != Legitimate) {
		H->cells[Pos].Info = Legitimate;
		H->cells[Pos].Data = key;
		return true;
	}
	else {
		//printf("键值已存在\n");
		return false;
	}
}
void Delete(HashTable H, ElementType key) {//在散列表中将元素key删除
	int i = Find(H, key);//在散列表中查找元素key
	if (H->cells[i].Info == Legitimate) {
		H->cells[i].Info = Deleted;
	}
	else return;//没找到给元素直接退出
}
int main() {
	int n, choice, lenth, a[1005] = { 0 };
	ElementType key;
	printf("请输入关键字的个数和散列表的长度：\n");
	scanf("%d %d", &n, &lenth);
	HashTable H = CreateTable(lenth);//创建散列表，定义大小为11
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i]);
		Insert(H, a[i]);
	}
	printf("创建的散列表的长度为：%d\n", H->TableSize);
	printf("下面是散列表中各位置对应的元素：\n");
	printf("-------------------------------------------\n");
	for (int i = 0; i < H->TableSize; i++) printf("%d:%d \n", i, H->cells[i].Data);
	printf("-------------------------------------------\n");
	printf("下面是查找散列表中各元素的查找次数：\n");
	double x = double(n) / double(H->TableSize), sum = 0;
	//计算成功查找的平均查找长度:
	for (int i = 0; i < n; i++) {
		sum += Find1(H, a[i]);
		printf("查找元素%2d的查找次数：%d\n", a[i], Find1(H, a[i]));
	}
	printf("总查找次数:%d\n", int(sum));
	printf("-------------------------------------------\n");
	double ASL = sum / double(n);
	printf("装填因子为：%.2lf\n", x);
	printf("查找成功的平均查找长度为:%.2lf\n", ASL);
	return 0;
}
/*
12 17
29 01 13 15 56 20 87 27 69 9 10 74
9 13
92 81 58 21 57 45 161 38 117
9 9
47 7 29 11 9 84 54 20 30
*/

运行结果：

 

 用分离链接法解决冲突

        已知线性表的关键字集合{21，11，13，25，48，6，39，83，30，96，108}，散列函数h(key)=key%11，采用分离链表法处理冲突，试给出散列表的结构，并计算该表查找成功的平均查找长度。

实现代码：

#include
#include
#define KEYLEGTH 1005
typedef int ElementType;
typedef struct LNode {//定义单链表的结构体
	ElementType Data;
	struct LNode* Next;
}*List;
typedef struct TblNode {//定义散列表结构体
	int TableSize;//定义散列表的最大长度
	List* Heads;//指向链表头结点的数组（指针）
}*HashTable;
int Hash(ElementType key, int TableSize) {
	return key % TableSize;
}
HashTable CreateTable(int TableSize) {//创建单链表的散列表
	HashTable H = (HashTable)malloc(sizeof(struct TblNode));
	H->TableSize = TableSize;
	H->Heads = (List*)malloc(sizeof(struct LNode) * H->TableSize);
	for (int i = 0; i < H->TableSize; i++) {
		H->Heads[i] = (List)malloc(sizeof(struct LNode));
		H->Heads[i]->Data = 0;
		H->Heads[i]->Next = NULL;
	}
	return H;
}
List Find(HashTable H, ElementType key) {
	int Pos = Hash(key, H->TableSize);
	List p = H->Heads[Pos];//指向第一个结点
	if (p == NULL)return NULL;
	while (p != NULL && p->Data != key) p = p->Next;//当指针不为空且链表元素不等于要查找的元素key
	return p;
}
int Find1(HashTable H, ElementType key) {//返回查找元素key的查找次数
	int i = key % H->TableSize, sum = 1;
	List p = H->Heads[i]->Next;
	while (p != NULL) {
		if (p->Data == key)return sum;
		else sum++;
		p = p->Next;
	}
	return sum;
}
bool Insert(HashTable H, ElementType key) {//将元素key插入散列表
	List p = Find(H, key);
	if (p == NULL) {//如果p为空，说明散列表中没有该元素，可以插入
		List q = (List)malloc(sizeof(struct LNode));
		if (q == NULL) return false;
		else {
			q->Data = key;
			int i = Hash(key, H->TableSize);
			q->Next = H->Heads[i]->Next;
			H->Heads[i]->Next = q;//头插法将元素插入链表
			return true;
		}
	}
	else {//否则元素已存在，直接退出
		printf("键值已存在\n");
		return false;
	}
}
void DestroyTable(HashTable H) {
	int i;
	List p, tmp;
	for (int i = 0; i < H->TableSize; i++) {//释放每个链表结点
		p = H->Heads[i]->Next;
		while (p != NULL) {
			tmp = p->Next;
			free(p);
			p = tmp;
		}
	}
	free(H->Heads);//释放头节点数组
	free(H);//释放散列表结点
}
int main() {
	int n, choice, lenth, a[1005] = { 0 };
	ElementType key;
	printf("请输入关键字的个数和散列表的长度：\n");
	scanf("%d %d", &n, &lenth);
	HashTable H = CreateTable(lenth);//创建散列表，定义大小为11
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i]);
		Insert(H, a[i]);
	}
	int m = n;
	printf("创建的散列表的长度为： % d\n", H->TableSize);
	printf("下面是散列表中各位置对应的元素：\n");
	printf("-------------------------------------------\n");
	for (int i = 0; i < H->TableSize; i++) {
		int flag = 0;
		List p = H->Heads[i]->Next;
		printf("%d:", i);
		while (p != NULL) {
			flag = 1;
			printf("%d ", p->Data);
			p = p->Next;
		}
		if (flag != 0) printf("\n");
		else { printf("无元素\n"); m--; }
	}
	printf("-------------------------------------------\n");
	printf("下面是查找散列表中各元素的冲突次数：\n");
	double x = double(m) / double(H->TableSize), sum = 0;
	//计算成功查找的平均查找长度:
	for (int i = 0; i < n; i++) {
		sum += Find1(H, a[i]);
		printf("查找元素%03d的查找次数：%d\n", a[i], Find1(H, a[i]));
	}
	printf("总查找次数:%d\n", int(sum));
	printf("-------------------------------------------\n");
	double ASL = sum / double(n);
	printf("装填因子为：%.2lf\n", x);
	printf("查找成功的平均查找长度为:%.2lf\n", ASL);
	return 0;
}
/*
12 17
29 01 13 15 56 20 87 27 69 9 10 74

9 13
92 81 58 21 57 45 161 38 117

11 11
21 11 13 25 48 6 39 83 30 96 108
*/

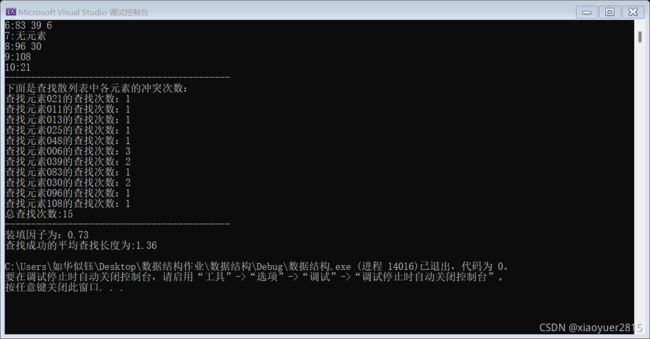
运行结果：

 结语

        嗯，没时间实现散列表的其它操作了，只是简单的创建并遍历了一下散列表，有时间再写一下散列表的删除这些操作。（其实已经写了删除这些操作，但是没有验证）