ML 线性回归Linear Regression

线性回归

Linear Regression

MOOC机器学习课程学习笔记

1 单变量线性回归Linear Regression with One Variable

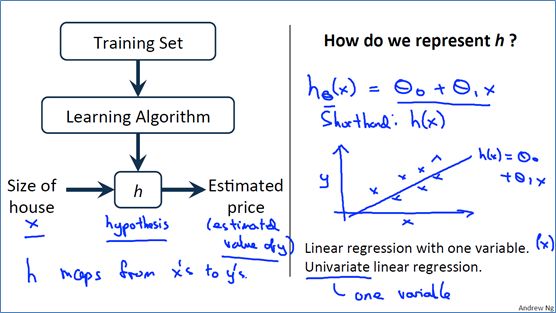
1.1 模型表达Model Representation

一个实际问题，我们可以对其进行数据建模。在机器学习中模型函数一般称为hypothsis。这里假设h为：

我们从简单的单变量线性回归模型开始学习。

1.2 代价函数Cost Function

代价函数也有很多种，下面的是平方误差Squared error function：

其中，m为训练集的个数。该代价函数在线性回归模型中很常用。其目标最小化假设函数hypothesis计算出来的目标值和训练集的实际值的误差值。

下面我们对假设函数进行简化，假设只有一个参数，通过假设函数和代价函数的公式，我们可以画出下面的图。注意，假设函数是以为变量，而代价函数是以为变量。

如果我们还是保持两个变量，那么代价函数画出来的图应该就是一个三维图形，高度就是值

通常我们会用contour plots或称为contour figures来表示。如下图

Contour figures中的那三个点的值是一样的，最中心的那个点的值最小，有些等高线的意思。

1.3 梯度下降Gradient Descent

下面将学习梯度下降这种算法来学习假设函数的参数。这里需要注意的是，梯度下降更新参数值是正确的应该是所有参数同时更新。

我们将参数简化到一个可以看到，梯度下降公式根据目前点沿切线方向以步长（也就是学习速率）下降，其实就是将参数朝最小值方向变化。

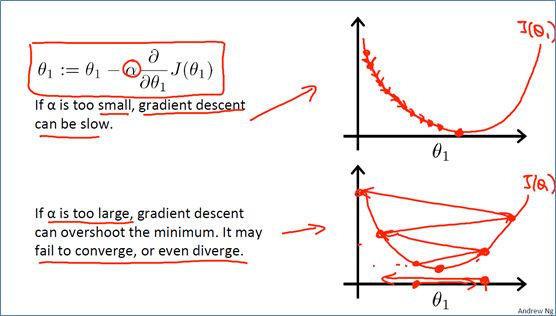
这里学习速率对其结果有比较大影响，若太小，则下降的速率很慢，要进行很多步才能到达最小值；若太大，有可能会产生震荡，无法收敛。

 

下面我们来对线性回归使用梯度下降算法，回忆下线性回归的假设函数与代价函数：

根据梯度下降的公式，对代价函数求偏导，可以算出线性回归中参数更新的公式：

在线性回归中，损失函数是一个凸函数（convex function）所以不存在局部最优点，一定能算出全局最优点。而且在这里我们每次对参数更新，都是对所有训练数据集求和，这种梯度下降方法叫做批量梯度下降（Batch Gradient Descent），当然也有其他的方法。

2 多元线性回归 Linear Regression with Multiple Variables

2.1 多特征Multiple Features

在现实问题中，我们变量往往不止一个，我们将单变量的线性回归推广到多变量。首先来看看我们的模型表达，也就是假设函数。假设我们有4个变量，那么我们定义个记号如下：

再推广到n个变量，我们的假设函数公式为： 。用向量表示的话：

2.2 多元梯度下降 Gradient Descent for Multiple Variables

    对多元的假设函数求偏导，可以得出多元参数梯度下降的更新公式：

当特征是多元的时候，有可能其中某些特征和另一些特征都不在一个数量级上，比如一个特征的范围在[0,1]而另一个特征的范围在[1000,2000]那么这样直接使用梯度下降会导致收敛速度十分慢。

对此，我们可以使用特征缩放（Feature Scaling）技术来加快梯度下降的收敛速度。其中一种比较常用的方法是均值标准化（Mean normalization）

其中 是训练集中特征的均值， 可以是max-min也可以是该类特征的标准差。其中对特征进行放缩并不需要十分精确，只要在相似的范围就可以了，它只是为了使梯度下降收敛更快。

在梯度下降中还有一个十分重要的超参数就是学习速率 ，它不仅会影响到收敛速度，而且可能会到时梯度下降无法收敛。那么如何选择学习速率对于我们来说十分重要。通常我们应该在调试时，绘制出代价函数随迭代次数的变化图。

如果这个代价函数每一步并没有下降，反而上升的话，我们都应该去选择更小的学习速率。如果学习速率太小的话，收敛速率会很慢。在挑选学习速率时，经验是按照3倍的增长通过绘制不同的代价函数图，来寻找一个合适的学习速率。

2.3 特征和多项式回归Features and Polynomial Regression

由于问题的复杂性，很多时候我们不可能只有一条直线去拟合就能得到很好的效果。而且不同的特征对于模型会有不同的效果。对于特征选择以后的教程会讲到，这里只是告诉我们可以通过深入的研究，对不同的特征和函数图像的理解，去选择不同的模型来进行拟合。

2.4 标准方程法 Normal Equation

    在求最小化代价函数的参数时，除了用梯度下降法，其实还有其他不少方法，这里介绍通过标注方程Normal Equation，不用迭代直接求出参数。

标准方程：

和梯度下降法相比较，标准方程法不用去选择学习速率，而且不用迭代，但是需要计算特征矩阵的拟，如果特征数很大的话，那么标准方程法计算就十分慢了。所以我们可以根据实际问题特征数量n的大小来选择使用梯度下降还是标准方程方法。

在线性回归中很少会出现不可逆的情况，但是也是会出现的，一般是下面的情况导致不可逆。

我们在使用matlab函数编程时，可以使用pinv函数来求其拟，pinv与inv函数的主要区别在于pinv是伪求逆函数，即使其拟不存在，也可以求解。

练习部分代码

1 特征缩放代码

 1 function [X_norm, mu, sigma] = featureNormalize(X)
 2 %FEATURENORMALIZE Normalizes the features in X 
 3 %   FEATURENORMALIZE(X) returns a normalized version of X where
 4 %   the mean value of each feature is 0 and the standard deviation
 5 %   is 1. This is often a good preprocessing step to do when
 6 %   working with learning algorithms.
 7 
 8 % You need to set these values correctly
 9 X_norm = X;
10 mu = zeros(1, size(X, 2));
11 sigma = zeros(1, size(X, 2));
12 num_fea=size(X,2);
13 
14 % ====================== YOUR CODE HERE ======================
15 % Instructions: First, for each feature dimension, compute the mean
16 %               of the feature and subtract it from the dataset,
17 %               storing the mean value in mu. Next, compute the 
18 %               standard deviation of each feature and divide
19 %               each feature by it's standard deviation, storing
20 %               the standard deviation in sigma. 
21 %
22 %               Note that X is a matrix where each column is a 
23 %               feature and each row is an example. You need 
24 %               to perform the normalization separately for 
25 %               each feature. 
26 %
27 % Hint: You might find the 'mean' and 'std' functions useful.
28 %    
29 for i=1:num_fea
30     mu(i)=mean(X(:,i));
31     sigma(i)=std(X(:,i));
32     X_norm(:,i)=(X(:,i)-mu(i))./sigma(i);
33 end
34 
35 % ============================================================
36 
37 end

2 计算代价函数

 1 function J = computeCostMulti(X, y, theta)
 2 %COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
 3 %   J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
 4 %   parameter for linear regression to fit the data points in X and y
 5 
 6 % Initialize some useful values
 7 m = length(y); % number of training examples
 8 
 9 % You need to return the following variables correctly 
10 J = 0;
11 
12 % ====================== YOUR CODE HERE ======================
13 % Instructions: Compute the cost of a particular choice of theta
14 %               You should set J to the cost.
15 
16 temp=X*theta-y;
17 J=1/(2*m)*temp'*temp;
18 
19 % =========================================================================
20 
21 end

3 梯度下降
注意向量化的表达

 1 function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
 2 %GRADIENTDESCENTMULTI Performs gradient descent to learn theta
 3 %   theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
 4 %   taking num_iters gradient steps with learning rate alpha
 5 
 6 % Initialize some useful values
 7 m = length(y); % number of training examples
 8 J_history = zeros(num_iters, 1);
 9 
10 for iter = 1:num_iters
11 
12     % ====================== YOUR CODE HERE ======================
13     % Instructions: Perform a single gradient step on the parameter vector
14     %               theta. 
15     %
16     % Hint: While debugging, it can be useful to print out the values
17     %       of the cost function (computeCostMulti) and gradient here.
18     %
19 
20     h_error=X*theta-y;
21     error=(alpha/m).*(h_error'*X);
22     theta=theta-error';
23 
24     % ============================================================
25 
26     % Save the cost J in every iteration    
27     J_history(iter) = computeCostMulti(X, y, theta);
28 
29 end
30 
31 end

4 主函数

需要注意的是如果在训练时进行了特征缩放，那么在测试时也一定要记得进行同样的特征缩放。

%% Machine Learning Online Class
%  Exercise 1: Linear regression with multiple variables
%
%  Instructions
%  ------------
% 
%  This file contains code that helps you get started on the
%  linear regression exercise. 
%
%  You will need to complete the following functions in this 
%  exericse:
%
%     warmUpExercise.m
%     plotData.m
%     gradientDescent.m
%     computeCost.m
%     gradientDescentMulti.m
%     computeCostMulti.m
%     featureNormalize.m
%     normalEqn.m
%
%  For this part of the exercise, you will need to change some
%  parts of the code below for various experiments (e.g., changing
%  learning rates).
%

%% Initialization

%% ================ Part 1: Feature Normalization ================

%% Clear and Close Figures
clear ; close all; clc

fprintf('Loading data ...\n');

%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');

fprintf('Program paused. Press enter to continue.\n');
pause;

% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');

[X mu sigma] = featureNormalize(X);

% Add intercept term to X
X = [ones(m, 1) X];


%% ================ Part 2: Gradient Descent ================

% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
%               code that runs gradient descent with a particular
%               learning rate (alpha). 
%
%               Your task is to first make sure that your functions - 
%               computeCost and gradientDescent already work with 
%               this starter code and support multiple variables.
%
%               After that, try running gradient descent with 
%               different values of alpha and see which one gives
%               you the best result.
%
%               Finally, you should complete the code at the end
%               to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
%       graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%

fprintf('Running gradient descent ...\n');

% Choose some alpha value
alpha = 0.01;
num_iters = 400;

% Init Theta and Run Gradient Descent 
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);

% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
hold on;

% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');

% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
x=[1 1650 3];
x(2)=(x(2)-mu(1))/sigma(1);
x(3)=(x(3)-mu(2))/sigma(2);
price = x*theta; %这里要注意，因为梯度下降使用了特征缩放，这里测试时也一定记得要做同样的特征缩放。

% ============================================================

fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
         '(using gradient descent):\n $%f\n'], price);

fprintf('Program paused. Press enter to continue.\n');
pause;

%% ================ Part 3: Normal Equations ================

fprintf('Solving with normal equations...\n');

% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form 
%               solution for linear regression using the normal
%               equations. You should complete the code in 
%               normalEqn.m
%
%               After doing so, you should complete this code 
%               to predict the price of a 1650 sq-ft, 3 br house.
%

%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);

% Add intercept term to X
X = [ones(m, 1) X];

% Calculate the parameters from the normal equation
theta = normalEqn(X, y);

% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');


% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = [1 1650 3]*theta; % You should change this


% ============================================================

fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
         '(using normal equations):\n $%f\n'], price);

 

转载于:https://www.cnblogs.com/robert-dlut/p/4285387.html