知识图谱顶会论文(IJCAI-2022) TEMP：多跳推理的类型感知嵌入

IJCAI-TEMP：知识图谱上多跳推理的类型感知嵌入

论文题目: Type-aware Embeddings for Multi-Hop Reasoning over Knowledge Graphs

论文会议: IJCAI 2022

论文地址: https://arxiv.org/pdf/2205.0078

• IJCAI-TEMP：知识图谱上多跳推理的类型感知嵌入
  • 摘要
  • 1.引言
  • 2.相关工作
    • 2.1 查询嵌入(QE)
    • 2.2 基于路径的方法
    • 2.3 归纳式KGC
    • 2.4 类型感知任务
  • 3.背景
  • 4.语义丰富嵌入
    • 4.1 TER：类型感知的实体表示
    • 4.2 TRR：类型感知的关系表示
      • 4.2.1 Step 1: 构造类型图
      • 4.2.2 Step 2: 关系类型聚合
      • 4.2.3 Step 3: 成对表示集成

摘要

由于传统的子图匹配方法不能很好地处理噪声和缺失信息，现实生活中的知识图(KGs)上的多跳推理是一个极具挑战性的问题。为了解决这个问题，最近流行一种很有前景的方法来替代传统的子图匹配方法，该方法通过将逻辑查询和KG联合嵌入到低维空间中来识别预测的实体。然而，现有的方法忽略了KG中固有的关键语义知识，例如类型信息。为了利用类型信息，我们提出了一种新颖的类型感知消息传递(TEMP)模型，它增强了查询中的实体和关系表示，同时改进了泛化、演绎和归纳推理。值得注意的是，TEMP 是一种即插即用的模型，可以很容易地整合到现有的基于嵌入的模型中以提高它们的性能。对三个真实世界数据集的广泛实验证明了TEMP的有效性。

1.引言

近年来，在大规模不完全知识图上回答一阶逻辑(FOL)查询的多跳推理问题在AI领域引起了广泛关注。传统的子图匹配方法在回答查询时面临的一个主要挑战是KG不可避免地是不完整的和有噪声的。事实上，当数据类型和三元组在KG中不完整时，在正常的演绎推理下不能保证找到正确答案，从而导致空答案或错误答案。另一个问题是它们内在的高计算复杂度，因为它们需要跟踪推理路径上出现的所有中间实体，导致指数膨胀。例如，要回答图1所示的查询“列出举办过夏季奥运会的亚洲国家的总统”，我们需要两个遍历步骤(其他查询需要更多的遍历步骤)：一个是确定举办过夏季奥运会的国家，另一个是确定其中的亚洲国家，每个国家都产生中间国家。

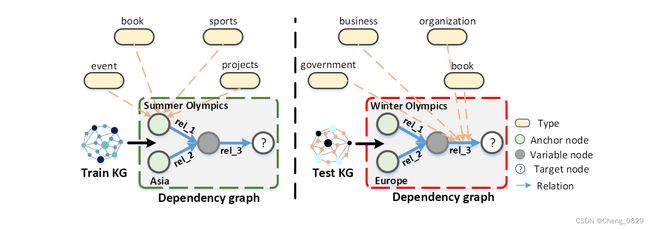
图1： 用于FOL查询的归纳设置。左侧显示查询 “列出举办过夏季奥运会的亚洲国家的总统” ；右侧显示了 “列出举办过冬奥会的欧洲国家的总统” 的查询。rel_1、rel_2 和 rel_3 分别表示关系 Hold 、Locate和President of。

为了解决这些挑战，最近流行一种用于查询回答的查询嵌入(QE)方法来替代子图匹配方法。其主要思想是将实体和查询嵌入到联合的低维向量空间中，以便回答查询的实体接近查询的嵌入。目前已经提出了几种用于查询回答的QE模型，表现出非常有前景的性能。然而，这些模型未能利用KG中固有的语义知识，如实体描述或实体类型信息。引入类型信息的优点是:

1. 可以丰富实体或关系的表示能力;例如，在sports event上下文中的类型信息sports和event可以丰富实体Summer Olympics的表示(参见图1)。
2. 它还可以帮助解决一些归纳式查询回答问题，即在训练时无法观察到测试查询中使用的实体;例如，对于图1中的查询: “列出举办过夏季奥运会的亚洲国家的总统” 和 “列出举办过冬季奥运会的欧洲国家的总统” ，它们是由两个具有互不相干的实体集的KG生成的，我们分别称为Train KG和Test KG。即使夏季奥运会和冬季奥运会的实体不同，它们也有类似的类型信息，如体育和事件。因此，在使用类型信息表示实体之后，与由Train KG生成的查询相关联的模型对由Test KG生成的查询也有效。

本文的目标是引入一个类型感知的即插即用模型，该模型充分利用了知识图中的类型信息，并且可以很容易地嵌入到现有的基于QE的模型中。为此，我们提出了一个新的类型感知消息传递(TEMP)模型，它包含两个关键组件。

1. 类型感知实体表示(TER)：聚合实体类型信息以加强它们的向量表示(参见4.1节)。
2. 类型感知关系表示(TRR)：使用实体类型信息来构建全局类型图以增强关系表示，并同时将其与类型表示以及现有实体类型信息集成起来(参见第4.2节)。

重要的是，有些查询在查询路径中有可变节点(参见图1)，这增加了链中后续推理步骤的难度，因为变量节点是未知的。为了解决这个问题，TRR组件采用了一种双向机制作为锚节点来监督查询路径中的关系，反之亦然。此外，如前所述，在使用类型信息表示实体和关系之后，由于新实体或关系的出现不会影响基于类型的表示，因此模型具有内在的归纳性。

我们的主要贡献总结如下：

1. 我们提出了TEMP，一个新的类型感知的即插即用模型，用于KGs上的多跳推理，它可以很容易地集成到现有的基于查询嵌入(QE)的模型中。
2. 在TEMP中，我们设计了一种新的双向注意力集成机制，它集成了{实体、关系、类型}信息之间的两两依赖关系，即使在没有域和范围等数据模式公理的情况下也是如此。
3. 大量的实验表明，在将TEMP纳入四个最先进的基准模型后，它们的泛化、演绎和归纳推理能力在三个基准数据集上得到了稳定的和显著的提高。

数据、代码和含附录的扩展版本可在https://github.com/zhiweihu1103/QE-TEMP获得。

2.相关工作

2.1 查询嵌入(QE)

QE模型首先将实体和一阶逻辑(FOL)查询嵌入到联合的低维向量空间中，然后在潜在嵌入空间中计算实体表示和查询表示之间的相似度分数。一般来说，根据嵌入空间的类型，基于QE的方法可以分为四类:

1. 基于几何的方法，如GQE、Q2B、HypE和ConE，将逻辑查询和KG实体分别作为点、盒、双曲和圆锥形状嵌入几何向量空间;
2. 基于分布的方法，如BETAE，将查询嵌入到有界的贝塔分布；以及PERM，使用高斯密度对KGs进行推理;
3. 基于逻辑的方法，将所谓的集合逻辑与FOL联系起来;
4. 基于神经的方法，例如EMQL，使用神经检索实现逻辑操作。

考虑到基于QE的方法是当前复杂问答(CQA)领域的主流，我们主要关注如何构建一个即插即用模型来嵌入现有基于QE的方法的类型信息。

2.2 基于路径的方法

除了基于QE的方法，基于路径的方法是CQA的另一种方法，但它面临着搜索空间随跳数呈指数增长的问题。例如，CQD方法使用束搜索方法显式跟踪中间实体，并通过t范数反复结合来自预训练链接预测器的分数，在跟踪中间实体时搜索答案。但是，CQD方法不支持完整的FOL查询集。

t范数(t-norm)：也称三角范数，是一种用于概率度量空间框架和多值逻辑，特别是模糊逻辑的二元运算。
最小t范数：$T_{min}(a,b)=mina,b$
乘积t范数：$T_{prob}(a,b)=a\cdot b$
其余信息参见https://en.wikipedia.org/wiki/T-norm

2.3 归纳式KGC

在KGC的上下文中，有一些基于归纳设置的工作，在训练阶段看不到测试实体。根据使用的信息来源，它们可以分为两类：使用图结构信息，例如子图或拓扑结构；或使用外部信息，例如实体的文本描述。然而，所有这些方法都专注于归纳式KGC任务，可以将其视为回答更简单的单跳查询。

2.4 类型感知任务

类型信息以前被用于其他任务，如KGC或实体类型化。然而，这些工作不能直接用于回答FOL查询，因为这需要多跳推理，产生中间不确定实体。

3.背景

在本文中，知识图用图结构数据(如RDF)的标准格式表示。知识图$\mathcal{G}$是一个元组$(\mathcal{E},\mathcal{R},\mathcal{C},\mathcal{T})$，其中$\mathcal{E}$是一组实体，$\mathcal{R}$是一组关系类型，$\mathcal{C}$是一组实体类型，$\mathcal{T}$是一组三元组。$\mathcal{T}$中的三元组要么是关系断言$(h,r,t)$，其中$h,t\in \mathcal{E}$分别是三元组的头尾实体，$r\in \mathcal{R}$是连接头尾实体的三元组的边，要么是实体类型断言$(e,type,c)$，其中$e\in \mathcal{E}$是实体，$c\in \mathcal{C}$是实体类型，$type$是关系实例。

我们考虑使用存在量词(∃)、合取(∧)、析取(∨)和否定(¬)来操作FOL查询，我们将以析取范式处理FOL查询，即表示为连词的析取。为了引入FOL查询，我们假设${\mathcal{V}}_a\subset \mathcal{E}$表示一组不可变输入锚实体，$V_1,...,V_m$表示存在量词的变量，$V_{?}$是目标变量。FOL查询Q是如下形式的公式：
$$\mathcal{Q}[V_{?}]=V_{?}.\exists V_1,...,V_m:c_1\vee c_2\vee ...\vee c_n$$
其中$c_i=e_{i1}\wedge ...\wedge e_{ik}$，k≤m使得每个$e_{ij}$具有以下形式之一：
$r(V_a,V),\neg r(V_a,V),r(V,V^{\prime }),\neg r(V,V^{\prime })$，其中$V_a\in {\mathcal{V}}_a,V\in \{V_{?},V_1,...V_m\},V^{\prime }\in \{V_1,...V_m\},V\ne V^{\prime }$

注：上述数学式表达的意思可以看图得出，即代表起始节点(锚节点)的$V_a$和中间可变节点$V/V^{\prime }$建立关系，而由于不确定是多跳推理还是单跳推理，所以要先和包含目标变量$V_{?}$的$V$建立关系

查询$\mathcal{Q}$的依赖图(DG)是$\mathcal{Q}$的图形化表示，其中节点对应于$\mathcal{Q}$中的变量或非变量参数，而边对应于$\mathcal{Q}$中的关系。图1列出了DG的示例。

我们感兴趣的是在KGs上回答查询Q的多跳推理问题，该问题的目的是如果$\mathcal{Q}[a]$保持真值，能找到一组实体 [$\mathcal{Q}$] $\subseteq \mathcal{E}$，使得$a\in$[$\mathcal{Q}$]。

4.语义丰富嵌入

我们的模型TEMP由两个子模型组成：类型感知实体表示(TER)和类型感知关系表示(TRR)，前者使用实体的类型信息来丰富其向量表示，后者进一步集成实体表示、关系类型和关系表示以同时加强实体和关系向量表示。有趣的是，由于我们只利用类型信息来执行实体和关系的深入描述，而不修改现有基于QE的模型的训练目标，因此可以以即插即用的方式轻松地将TEMP嵌入其中。

4.1 TER：类型感知的实体表示

TER背后的主要直觉是，实体的类型提供了一些有价值的信息，比如它在KG中的表示内容。例如，如果一个实体包含sports/multi - event tournament、time/event、olympics/olympic games等类型，那么可以推断对应的实体代表Olympics。为了捕捉这种直觉，我们设计了一个可迭代的多个高速神经网络层来聚合实体类型断言中的类型信息，以获得更准确和全面的表示。设${\mathcal{H}}_s^i\in {\mathbb{R}}^{d\times n}$表示迭代$i\ge 1$次时实体类型信息的隐藏状态(和4.2.2节不同)，其中$d$和$n$分别表示实体的向量大小和类型数量。给定实体的基于高速神经网络的**类型融合**表示可以计算如下:
$$g=\sigma \left(W_i{\mathcal{H}}_s^i+b_i\right)\text{\hspace{1em}(1)}$$
$${\mathcal{H}}_s^{i+1}=g\ast \left(W_i^{\prime }{\mathcal{H}}_s^i+b_i^{\prime }\right)+(1-g)\ast {\mathcal{H}}_s^i\text{\hspace{1em}(2)}$$
$${\mathcal{H}}_s^K=W{\mathcal{H}}_s^K+b\text{\hspace{1em}(3)}$$

式(1)算出输出状态；式(2)用输出状态和隐藏状态共同算出下一层的隐藏状态；式(3)即为最终输出状态

其中，${\mathcal{H}}_s^1$是实体类型的初始特征，$\sigma$是一个基于元素的sigmoid函数，$\{W_i,W_i^{\prime }\}\in {\mathbb{R}}^{d\times d}$和$\{b_i,b_i^{\prime }\}\in {\mathbb{R}}^{d\times 1}$是可学习矩阵，$g\in {\mathbb{R}}^{d\times n}$是重置门。迭代K次(设K=2)后，实体类型信息的最终隐藏状态${\mathcal{H}}_s^K\in {\mathbb{R}}^{d\times n}$(经过线性运算得到最终输出状态${\mathcal{H}}_s^K\in {\mathbb{R}}^{d\times 1}$)作为给定实体类型的表示。我们进一步连接初始实体及其类型聚合表示，以获得增强的实体表示：
$${\mathcal{H}}^e=W^{\prime }[{\mathcal{H}}_s^K,{\mathcal{H}}_s^0]+b^{\prime }\text{\hspace{1em}(4)}$$

${\mathcal{H}}_s^K$是类型表示，${\mathcal{H}}^e$是实体表示

其中 [·] 为拼接函数，$W^{\prime }\in {\mathbb{R}}^{d\times d}$和$b^{\prime }\in {\mathbb{R}}^{d\times 1}$是要学习的参数。${\mathcal{H}}^e\in {\mathbb{R}}^{d\times 1}$是实体的最终表现形式。需要注意的是，如果是归纳推理，我们不会将初始实体信息${\mathcal{H}}_s^0$连接起来，因为在训练期间看到的实体不会在测试阶段出现。该过程显示在图2的顶部中心。

图2：TEMP 的架构。左上部分是查询“List of Asian countries which has lost Olympics”的依赖关系图，rel_1、rel_2、rel_3分别表示Hold、Locate和President的关系。

4.2 TRR：类型感知的关系表示

在实体上执行TER对于没有存在量词变量的查询非常有用。然而，对于带有链式存在变量(DG中的变量节点链)的查询，仅在锚实体或目标变量上执行TER是不够的。直观地看，问题在于长链推理过程中，锚实体与目标变量之间的相关性经过多次关系投影后可能不够强。此外，连续的关系投影可能导致搜索空间呈指数级增长，进一步增加了模型的复杂性。

我们首先观察到关系的类型与其在KG中的表示是相关的。例如，假设关系r有government/political_appointer和organization/role等类型，那么我们可以合理地推断关系r表示President of。在长链查询中，关系的类型增强有助于减少答案实体空间和由多个投影引起的级联错误。然而，在大多数现有的KG中，关系缺乏特定的类型注释(例如域和范围)。

1. 为了解决这个问题，我们在原始KG的基础上构建了一个新的类型图，其中类型作为节点，关系作为边(参见图2的左下及4.2.1节)。
2. 在接下来的步骤中，我们聚合了类型图上的类型信息，以获得对应于特定关系的类型嵌入(参见图2的左下及4.2.2节)。
3. 最后，我们通过双向注意力机制将实体表示、关系的聚合类型信息及其表示整合在一起，使中间变量节点能够感知锚节点或目标节点的信息以及推理链中关系的信息(见图2右侧及4.2.3节)。这将有助于避免长链推理导致锚节点与目标实体之间的联系减弱。

4.2.1 Step 1: 构造类型图

我们正式定义了一个类型图${\mathcal{G}}_{tp}$。设$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{C},\mathcal{T})$表示KG(各元素含义参见第3节)。对于关系$r\in \mathcal{R}$，${\mathcal{T}}_r\subseteq \mathcal{T}$表示r所在的的关系断言集。对于一个关系断言$\mathrm{t}\in {\bigcup }_{r\in R}{\mathcal{T}}_r$，$\mathrm{hd}(\mathrm{t})$和$\mathrm{tl}(\mathrm{t})$分别表示关系断言$\mathrm{t}$的头实体和尾实体，$\mathrm{t}{\mathrm{p}}_{\mathrm{t}}(hd(t))=\{c|(hd(t),type,c)\in \mathcal{T}\}$表示关系断言$\mathrm{t}$的头实体的类型集；$\mathrm{t}{\mathrm{p}}_{\mathrm{t}}(tl(t))$的定义类似。由于$r$可能出现在多个关系断言中，我们将通过取$r$所在的关系断言的头部实体的类型和尾部实体的类型的交集来计算$r$的类型信息。对于$r\in R$,我们定义：
$${\mathrm{tp}}_r^{\mathrm{hd}}(\mathcal{G})=\bigcap _{\mathrm{t}\in {\mathcal{T}}_r}{\mathrm{tp}}_{\mathrm{t}}(\mathrm{hd}(\mathrm{t})),{\mathrm{tp}}_r^{\mathrm{tl}}(\mathcal{G})=\bigcap _{\mathrm{t}\in {\mathcal{T}}_r}{\mathrm{tp}}_{\mathrm{t}}(\mathrm{tl}(\mathrm{t}))$$

另外，如果存在$\mathrm{t}\in {\mathcal{T}}_r$，我们通过设置$V={\bigcup }_{r\in R}{\mathrm{tp}}_r^{\mathrm{hd}}(\mathcal{G})\cup {\mathrm{tp}}_r^{\mathrm{tl}}(\mathcal{G}),E=\mathcal{R}$以及$(v,r,v^{\prime })\in T$来定义$\mathcal{G}=(V,E,T)$，使得$v={\mathrm{tp}}_{\mathrm{t}}(\mathrm{hd}(\mathrm{t}))$以及$v^{\prime }={\mathrm{tp}}_{\mathrm{t}}(\mathrm{tl}(\mathrm{t}))$

V是类型，E是边，T是头尾实体的类型-关系断言。

4.2.2 Step 2: 关系类型聚合

对于一个给定的关系$r\in E$，我们把与关系r有关的类型定义为${\mathrm{tp}}_r({\mathcal{G}}_{\mathrm{tp}})={\mathrm{tp}}_r^{\mathrm{hd}}(\mathcal{G})\cup {\mathrm{tp}}_r^{\mathrm{tl}}(\mathcal{G})$。我们在${\mathrm{tp}}_r({\mathcal{G}}_{\mathrm{tp}})$的元素上固定一个任意的线性顺序，并用${\mathrm{tp}}_r^i({\mathcal{G}}_{\mathrm{tp}})$表示第$i$种类型，其中$1\le i\le |{\mathrm{tp}}_r({\mathcal{G}}_{\mathrm{tp}})|$。

注意，并非${\mathrm{tp}}_r({\mathcal{G}}_{\mathrm{tp}})$中的所有类型都与回答给定的查询相关。例如，假设关系has_part包含类型{vehicle, animal, universe}，对于“猫的器官有哪些?”，我们应该给予动物类型更多的关注，但对于“哪些零件是汽车的部件?”“我们应该专注于车辆类型。

因此，我们不是简单地连接(或平均)与一个关系相关的所有类型信息，而是将关系类型聚合建模为一个注意力神经网络，定义为:
$${\mathcal{H}}^s=\sum _i{a}_i\odot {\mathcal{H}}_s^i\text{\hspace{1em}(5)}$$
$$a_i=\frac{\exp \left(\mathbf{MLP}\left({\mathcal{H}}_r^i\right)\right)}{{\sum }_j\exp \left(\mathbf{MLP}\left({\mathcal{H}}_r^j\right)\right)}\text{\hspace{1em}(6)}$$

${\mathcal{H}}^s$是聚合类型信息${\mathrm{tp}}_r({\mathcal{G}}_{\mathrm{tp}})$的向量表示；${\mathcal{H}}_s^i\in {\mathbb{R}}^{d\times 1}$是第$i$个类型${\mathrm{tp}}_r^i({\mathcal{G}}_{\mathrm{tp}})$的向量化表示(和4.1节不同)，初始化为维数d且$1\le i\le |{\mathrm{tp}}_r^i({\mathcal{G}}_{\mathrm{tp}})|$的均匀分布；$a_i\in {\mathbb{R}}^{d\times 1}$是对于所有$1\le j\le d$都满足${\sum }_{i=1}^n[a_i]j$的正向权值向量；并且$\mathbf{MLP}$(·)是一个${\mathbb{R}}^d\to {\mathbb{R}}^d$的多层感知器。

4.2.3 Step 3: 成对表示集成

在嵌入查询时，集成实体、关系和类型的信息有助于平滑决策边界，但这需要捕获KG中查询的目标匹配。例如，对于查询“哪些国家举办过夏季奥运会?”，我们需要关注“夏季奥运会”中“举办”的连接，而不是“观看”的连接。类似地，我们应该只考虑从“夏季奥运会”开始的“举办”连接，而不是其他的例如“世界杯”。为了在三元组$\{{\mathcal{H}}^e,{\mathcal{H}}^r,{\mathcal{H}}^s\}$ (${\mathcal{H}}^e$和${\mathcal{H}}^s$定义为式(4)和式(5)，${\mathcal{H}}^r$为初始化关系向量)中恰当地捕获这一限制，我们引入了一种双向注意力机制来集成表示对(“实体-关系”、“实体-类型”和“关系-类型”)的每个状态。在这里，我们将展示如何为“实体-关系”对做到这一点：${\mathcal{H}}^e$与${\mathcal{H}}^r$之间的双向集成表示可计算为：
$${\mathcal{G}}^{er}=\mathrm{Relu}\left(W_1\left[\begin{array}{l}{\mathcal{H}}^e\ominus {\mathcal{H}}^r\\ {\mathcal{H}}^e\otimes {\mathcal{H}}^r\end{array}\right]+b_1\right)\text{\hspace{1em}(7)}$$
$${\mathcal{G}}^{re}=\mathrm{Relu}\left(W_2\left[\begin{array}{l}{\mathcal{H}}^r\ominus {\mathcal{H}}^e\\ {\mathcal{H}}^r\otimes {\mathcal{H}}^e\end{array}\right]+b_2\right)\text{\hspace{1em}(8)}$$

其中$\{W_1,W_2\}\in {\mathbb{R}}^{2d\times 2d}$和$\{b_1,b_2\}\in {\mathbb{R}}^{2d\times 1}$是可学习的参数。我们使用元素减法⊖和元素乘法⊗来构建更好的匹配表示。${\mathcal{G}}^{er}\in R^{2d\times 1}$是整合关系信息到实体的结果，${\mathcal{G}}^{re}\in R^{2d\times 1}$都是整合实体信息到关系的结果。通过实体和关系的双向集成，我们同时获得了关系感知的实体表示${\mathcal{G}}^{er}$和实体感知的关系表示${\mathcal{G}}^{re}$，捕获了实体和关系之间的交互。

然后我们使用门控机制来结合双向融合产生的结果，因为它更好地调节了信息流。以实体融合表示为例，使用关系感知实体${\mathcal{G}}^{er}$和类型感知实体${\mathcal{G}}^{es}$表示作为输入，实体的最终表示计算为：
$$g=\sigma (W_3{\mathcal{G}}^{er}+W_4{\mathcal{G}}^{es}+b_3+b_4)\text{\hspace{1em}(9)}$$
$${\mathcal{G}}^e=g\ast {\mathcal{G}}^{er}+(1-g)\ast {\mathcal{G}}^{es}\text{\hspace{1em}(10)}$$

其中$\{W_3,W_4\}\in {\mathbb{R}}^{2d\times 2d}$和$\{b_3,b_4\}\in {\mathbb{R}}^{2d\times 1}$是可学习的参数。$g$是重置门，${\mathcal{G}}^e\in {\mathbb{R}}^{2d\times 1}$是实体的最终表示。

为了把融合特征转化为初始的向量大小，我们使用一个线形层：
$$\overline{{\mathcal{H}}^e}=W_5{\mathcal{G}}^e+b_5\text{\hspace{1em}(11)}$$
其中$W_5\in {\mathbb{R}}^{d\times 2d}$和$b_5\in {\mathbb{R}}^{d\times 1}$是可学习的参数。$\overline{{\mathcal{H}}^e}$是实体由关系和类型增强的最终表示。