Loam算法详解（配合开源代码aloam）

参考论文：LOAM: Lidar Odometry and Mapping in Real-time
代码：A-LOAM
Ubuntu 18.04 + ROS Melodic + eigen 3.3.4 + PCL 1.8.1 + ceres 2.0 + A-LOAM 配置

LOAM算法是激光slam中一个经典的开源框架，结合qin tong 博士的开源代码a-loam，对其原理及代码实现简要介绍如下：

LOAM算法的总体框架如下图所示：

除了左侧的硬件采集数据之外，LOAM算法本身主要包括图中标记的-四个部分。该算法的关键想法是把实时定位与测图这一同时寻找优化大量变量的复杂问题进行区分，通过两个算法来进行解决。首先，使用一个高频、低精度的里程计来估计LiDAR的位姿，并以此结果去除实验过程中产生的运动畸变（假设为匀速运动）。另外，使用一个低频、高精度的里程计算法来改善LiDAR位姿的精度，并输出全局坐标系下的地图。

1 LiDAR硬件

LiDAR硬件在采集过程中不断发布点云数据（10 HZ）,以符号$P_k$表示在第K帧接收到的点云数据。
$L$是局部激光坐标系，坐标原点在Lidar的几何中心,以符号$X_{(k,i)}^L$表示在第$K$帧中的 $i$ 点在局部坐标系下的坐标。
$W$ 是全局坐标系，坐标原点在Lidar的起始位置,以符号$X_{(k,i)}^W$表示在第$K$帧中的 $i$ 点在全局坐标系下的坐标。

2 Point Cloud Registration

这一部分中从LiDAR硬件中接收原始点云数据，接着进行预处理（去除噪声点、无效点）并按照扫描线号进行区分，存储在一个vector中。随后，对点云数据进行处理，发布sharp、less_sharp、flat、less_flat四种类型的特征点，如下图中所示：

分别介绍LiDAR点云预处理与特征点提取两部分内容:

2.1 LiDAR点云预处理

传感器获得的数据可能在一些点的坐标中为NaN（不是数）值, 一个NaNs表明测量传感器距离到该点的距离值是有问题的，可能是因为传感器太近或太远，或者因为表面反射。那么当存在无效点云的NaNs值作为算法的输入的时候，可能会引起很多问题，使用PCL自带的函数进行去除。

随后，去除原始数据中距离很近的点，即相邻点间小于仪器测量的分辨率，这里设置MINIMUM_RANGE为0.1 m。

进行上述处理后，计算每个点的scanID并存储在对应的laserCloudScans变量中。


此外，还计算了当前点在一帧数据中的相对时间（时间比例），存放在intensity中（后续修正运动畸变时使用）。

2.2 提取特征点

在文章中描述了通过公式（1）来描述局部表面的平滑程度，其中S表示选取的一个周围点集，$X_{(k,i)}^L$表示当前点，$X_{(k,j)}^L$表示近邻点。

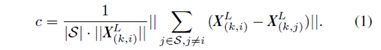
若c值较大，则代表当前点与周围点的差距较大，曲率较高，代表为一个边缘点（也就是代码中的sharp点）。
若c值较小，则代表当前点与周围点的差距较小，曲率较低，代表为一个平面点（也就是代码中的flat点）。
通过如下代码计算公式（1），当前点的前后5个点组成点云集合$S$。

在选择特征点的过程中，我们还想让其均匀分布，所以文章中计划把每个扫描分为4个部分（代码中分为了6个部分），同时每个子集区域中选取2个sharp点和4个flat点。

此外，为了避免选中不稳定的特征点，作者还讨论了下图中的两种情况要进行避免。1）左图(a)中的B点在一个几乎与激光束平行的表面上。2）右图(b)中的A点在被遮挡区域的边缘。

3 Lidar odometry

3.1 寻找特征点对应关系

假设一个扫描k的开始时间戳为$t_k$，在第$k$帧扫描结束接收到的点云为$P_k$（左侧第一条蓝线）,其被投影到$t_{(k+1)}$时间戳，用${\overline{P}}_k$表示（即中间的绿线），同时在下一个扫描$k+1$中获取的数据为$P_{(k+1)}$（图中的橙线）。

（注意：由于假设为匀速运动，所以上图中可以用直线来表示每一帧扫描的点云数据。）

现在，假设我们有了${\overline{P}}_k$和$P_{(k+1)}$两个点云数据集，基于此来寻找两个点云数据之间的对应关系。
首先，对$P_{(k+1)}$采用2.2节中提取特征点的方法找到两个特征点集，边缘点$E_{(k+1)}$和平面点$H_{(k+1)}$。其次，对${\overline{P}}_k$进行kd-tree索引，并在${\overline{P}}_k$中找到每个边缘点对应的边缘线（两个点，左图(a)）与每个平面点对应的面片（三个点，右图(b)）。

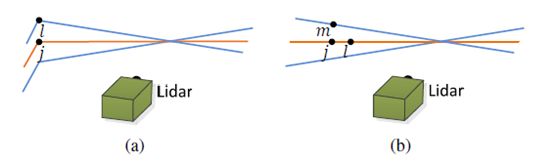
利用向量叉乘，获取点$i$到直线$ij$的距离，以及点$i$到平面$ljm$的距离。计算公式分别为：



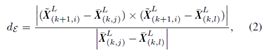
前述假设LiDAR在一个扫描中角速度和线速度均为匀速运动，所以能够对计算出的位姿进行线性插值。假设$T_{(k,i)}^L$为[$t_{(k+1)}$,$t$]两帧点云数据之间的位姿变换（6-DoF），给定一个点i , i∈$P_{(k+1)}$，其获取的时间戳为$t_i$，[$t_{(k+1)}$,$t_i$]之间的变换为$T_{(k+1,i)}^L$并可以通过下式进行计算。



在每一次迭代过程中均把$P_{(k+1)}$中的点i投影到该帧数据的起始点$t_{(k+1)}$，然后再与$P_k$中的点进行匹配。
假设$X_{((k+1,i))}^L$为投影之前的i点坐标，$X_{((k+1,i))}^L$为投影到起始点$t_{(k+1)}$之后的i点坐标，则两者之间存在如下关系。
综合考虑前述的公式2与公式3，得到以下公式9与公式10：


综合公式9与公式10，得到：

式11中每一行均为一个特征点及对应的边缘线或平面面片，对公式11中的非线性函数进行优化，不断迭代使得$d$最小。

3.2 Lidar odometry算法总结

Lidar odometry算法如下所示，以上一帧点云${\overline{P}}_k$，逐渐增长的点云$P_{(k+1)}$，以及上一次迭代计算的位姿参数$T_{(k+1)}^L$作为输入（如果是一个扫描的开始则设置为0）。接着，从$P_{(k+1)}$中提取边缘点$E_{(k+1)}$和平面点$H_{(k+1)}$，对于每个边缘点/平面点，在上一帧点云${\overline{P}}_k$中找到其对应的边缘线/面片，建立公式11中的非线性函数，并进行优，若迭代达到收敛则输出$T_{(k+1)}^L$，若达到了扫描的终点则输出$T_{(k+1)}^L$和${\overline{P}}_{(k+1)}$。

4 Lidar Mapping

第3节中的里程计高频、低精度运行，其输出的位姿参数还需要进一步在后续的mapping中进行优化。
Mapping算法在每个扫描结束才运行一次，如在第$k+1$次扫描结束后，lidar odometry产生了一个没有畸变的点云${\overline{P}}_{(k+1)}$和一个位姿变换参数$T_{(k+1)}^L$（代表[$t_{(k+1)}$,$t_{(k+2)}$]之间的运动）。Mapping算法把点云${\overline{P}}_{(k+1)}$配准到全局坐标系$W$下，如下图中所示，假设$Q_k$为前$k$次扫描积累的数据所形成的点云地图，$T_k^W$为lidar在地图中最后一次扫描$k$到$k+1$处的变换位姿。随着lidar odometry的输出，Mapping算法不断扩展$T_k^W$为$T_{(k+1)}^W$（即扫描时间[$t_{(k+1)}$,$t_{(k+2)}$]范围的全局变换，并把${\overline{P}}_{(k+1)}$投影到全局坐标系下，得到${\overline{Q}}_{(k+1)}$。接着，通过不断优化$T_{(k+1)}^W$把${\overline{Q}}_{(k+1)}$匹配到地图$Q_k$中。

特征点提取方法与上述的2.2节相同（数量增加10倍，即为代码中的less_sharp点与less_flat点）。为了找到特征点之间的对应关系且提高运行效率，使用边长为10m的立方体代替全局地图（代码中是10105）。

取立方体中与${\overline{Q}}_{(k+1)}$相交的部分，建立3D kd-tree索引。在$Q_k$的特征点中选取点集S’，针对边缘点只保留S’中边缘线上的点，针对平面点，只保留S’中面片上的点。然后，计算点集S’的协方差矩阵M，并分解M得到特征值记为V，特征向量E。

如果S’分布在一条线段上，那么V中一个特征值就会明显比其他两个大， E中与较大特征值相对应的特征向量代表边缘线的方向。（一大两小，大方向）
如果S’分布在一个平面上，那么V中一个特征值就会明显比其他两个小， E中与较小特征值相对应的特征向量代表平面的朝向。（一小两大，小方向）
边缘线或平面块的位置通过点集S’的几何中心确定。

边缘线或平面块的位置通过点集S’的几何中心确定。

为了计算边缘点/平面点与其对应边缘线/面片之间的距离，在一个边缘线上选取两个点，在面片上选取三个点，分别通过公式2、3进行计算，并转换为公式9、10，组合为公式11中所示的非线性函数，进行优化。
边缘特征：

平面特征：

求解：

最后，把${\overline{Q}}_{(k+1)}$匹配到地图$Q_k$中时，考虑到点云的均匀分布，还对其进行了一个下采样。