4 线性分类

$$线性分类\{\begin{array}{l}硬分类(y\in \{0,1\})\{\begin{array}{l}感知机\\ 线性判别分析（FisherDiscriminantAnalysis(LDA:LinearDiscriminantAnalysis)）\end{array}\\ 软分类(y\in (0,1))\{\begin{array}{l}概率判别模型：LogisticRegression\\ 概率生成模型：\{\begin{array}{l}GaussianDiscriminantAnalysis（连续）\\ NaiveBayes（离散）\end{array}\end{array}\end{array}$$
$y=f(w^{T}x+b)$，其中f为激活函数

1 硬分类

分类结果是0或1

1.1 感知机

思想：错误驱动（数据分类错误的时候调整参数）
模型：
$f(x)=sign(w^{T}x),x\in {\mathbb{R}}^p,w\in {\mathbb{R}}^p$
其中$sign(a)=\{\begin{array}{l}+1,a\ge 0\\ -1,a<0\end{array}$

loss function:
分对类的情况是$\{\begin{array}{l}{y}_i=1,w^T{x}_i>0\\ y_i=-1,w^T{x}_i<0\end{array}\Rightarrow y_i{w}^T{x}_i>0$
因此分错类的情况是$y_i{w}^T{x}_i<0$，将分错类的情况取反相加作为loss。
$L(w)=\stackrel{n}{\sum _{i=1}}(-y_i{w}^T{x}_i)$

梯度${\nabla }_{w}L=-y_i{x}_i$
用SGD迭代求得最终w：（在线性可分的情况下）
$w^{(t+1)}\leftarrow w^{(t)}-\lambda {\nabla }_{w}L=w^{(t)}+\lambda y_i{x}_i$

1.2 Fisher(LDA)

Linear Discriminant Analysis\Fisher Discriminant Analysis
$$X=(x_1,...,x_n{)}^T=\left(\begin{array}{c}{x}_1^T\\ ⋮\\ x_n^T\end{array}\right)={\left(\begin{array}{ccc}{x}_{11}& ...& x_{1p}\\ ⋮& & ⋮\\ x_{n1}& ...& xnp\end{array}\right)}_{n\ast p}Y={\left(\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right)}_{n\ast 1}$$
$\{(x_i,y_i){\}}_{i=1}^n,x_i\in {\mathbb{R}}^p,y_i\in \{+1,-1\}$
其中设+1为类1，-1为类2。他们的均值方差分别是${\mu }_1,{\mu }_2,{\Sigma }_1,{\Sigma }_2$，那么：
$$\begin{gathered} \mu =\frac{1}{n}\stackrel{n}{\sum _{i=1}}{x}_i \\ \Sigma =\frac{1}{n}\stackrel{n}{\sum _{i=1}}(x_i-\mu )(x_i-\mu {)}^T \end{gathered}$$

思想：
类内方差小，类间距大
找到一个投影方式$w^{T}x$，原数据在这个投影上每个相同类的点聚在一起，不同类之间的间距很远。如下图，右侧的投影更好。然后设定一个阈值（判别边界）来分类。

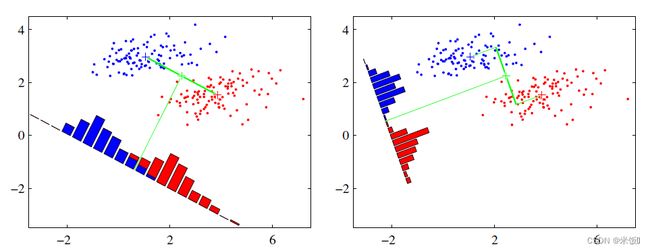
目标函数：
$$\begin{gathered} J(w)=\frac{({\mu }_1^{\prime }-{\mu }_2^{\prime }{)}^2}{{\Sigma }_1^{\prime }+{\Sigma }_2^{\prime }} \\ \hat{w}=arg\underset{w}{\max }J(w) \end{gathered}$$

经过投影后，新的均值和方差：
$$\begin{gathered} {\mu }^{\prime }=\frac{1}{n}\stackrel{n}{\sum _{i=1}}{w}^T{x}_i=w^T\ast \frac{1}{n}\stackrel{n}{\sum _{i=1}}{x}_i=w^T\mu \\ \begin{array}{rl}{\Sigma }^{\prime }& =\frac{1}{n}\stackrel{n}{\sum _{i=1}}(w^T{x}_i-{\mu }^{\prime })(w^T{x}_i-{\mu }^{\prime }{)}^T\\ & =\frac{1}{n}\stackrel{n}{\sum _{i=1}}(w^T{x}_i-w^T\mu )(w^T{x}_i-w^T\mu {)}^T\\ & =\frac{1}{n}\stackrel{n}{\sum _{i=1}}{w}^T(x_i-\mu )(x_i-\mu {)}^{T}w\\ & =w^T[\frac{1}{n}\stackrel{n}{\sum _{i=1}}(x_i-\mu )(x_i-\mu {)}^T]w\\ & =w^T\Sigma w\end{array} \end{gathered}$$
带入目标函数：
$$\begin{array}{rl}J(w)& =\frac{(w^T{\mu }_1-w^T{\mu }_2{)}^2}{w^T{\Sigma }_{1}w+w^T{\Sigma }_{2}w}\\ & =\frac{w^T({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^{T}w}{w^T({\Sigma }_1+{\Sigma }_2)w}\end{array}$$
令$S_b=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2),S_w={\Sigma }_1+{\Sigma }_2$
$$J(w)=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$$
对w求偏导
$$\begin{gathered} \frac{\partial J(w)}{\partial w}=\frac{2S_{b}w(w^T{S}_{w}w)-2(w^T{S}_{b}w)S_{w}w}{(w^T{S}_{w}w{)}^2}=0 \\ {S}_{b}w(w^T{S}_{w}w)=(w^T{S}_{b}w)S_{w}w\begin{array}{r}\end{array} \end{gathered}$$
其中$S_b,S_w$维度是p*p，$w^T$维度是1*p。因此$w^T{S}_{b}w,w^T{S}_{w}w$是标量。把标量放在一起有：
$$\frac{w^T{S}_{w}w}{w^T{S}_{b}w}{S}_{b}w=S_{w}w$$
这里是求投影的方向，不需要考虑投影的大小，也就是w的系数不重要，因此：
$$w=\frac{w^T{S}_{w}w}{w^T{S}_{b}w}{S}_w^{-1}{S}_{b}w\propto S_w^{-1}{S}_{b}w$$
将$S_b$带入：
$$w\propto S_w^{-1}({\mu }_1^{\prime }-{\mu }_2^{\prime })({\mu }_1^{\prime }-{\mu }_2^{\prime }{)}^{T}w$$
其中${\mu }^{\prime }$维度p*1,$w$维度p *1，因此$({\mu }_1^{\prime }-{\mu }_2^{\prime }{)}^{T}w$也是标量，所以：
$$w\propto S_w^{-1}({\mu }_1^{\prime }-{\mu }_2^{\prime })$$

2 软分类

分类结果是(0,1)之间的概率

2.1 概率判别模型

根据$P(Y|X)$直接建模，例如$y\in \{0,1\}$，那么求出$p(y=1|x),p(y=0|x)$比较大小即可。求的结果是判别边界。

2.1.1 逻辑回归

概率判别模型
sigmoid function：$\sigma (z)=\frac{1}{1+e^{-z}}$

sigmoid将结果映射到(0,1)，逻辑回归将结果映射为概率。
$$\begin{gathered} p_1=P(y=1|x)=\frac{1}{1+e^{-(w^{T}x)}} \\ {p}_0=P(y=0|x)=1-P(y=1|x)=\frac{e^{-(w^{T}x)}}{1+e^{-(w^{T}x)}} \end{gathered}$$
概率判别模型：
$$P(y|x)=p_1^y{p}_0^{1-y},y\in \{0,1\}$$
概率为：
$$L(w)=\prod _{i=1}^{N}P(y_i|x_i)$$
取对数：

上述过程中：
$$log\frac{p_1}{1-p_1}=log\frac{\frac{1}{1+e^{-(w^{T}x+b)}}}{\frac{e^{-(w^{T}x+b)}}{1+e^{-(w^{T}x+b)}}}=log\frac{1}{e^{-(w^{T}x+b)}}=w^{T}x+b$$
可以看到中间过程（第三行）和交叉熵是一样的，只是差一个负号：（交叉熵求的是函数最小值时的w或者说是p）

用MLE求解w
$$\begin{array}{rl}\hat{w}& =arg\underset{w}{\max }L(w)\\ & =arg\underset{w}{\max }\sum _{i=1}^N[y_i(w^T{x}_i)-log(1+e^{w^T{x}_i})]\end{array}$$
为了方便求解，一般将上式除样本数n来减少梯度爆炸出现的概率，并乘-1转化为求对小值问题，然后使用梯度下降：(求导略)
$$J(w)=min(-\frac{1}{n}\sum _{i=1}^N[y_i(w^T{x}_i)-log(1+e^{w^T{x}_i})])$$

2.2 概率生成模型

$$\underset{posterior}{P(y|x)}=\frac{P(x|y)P(y)}{P(x)}\propto \underset{likelihood}{P(x|y)}\underset{prior}{P(y)}=P(x,y)$$
$$\hat{y}=arg\underset{y\in (0,1)}{\max }P(y|x)=arg\underset{y}{\max }P(x|y)P(y)$$
对联合概率建模，关注数据的原始分布

2.2.1 Gaussian Discriminant Analysis

假设：（条件概率分布同方差）
$y\sim Bernoulli(p)\Rightarrow \begin{array}{clc}y& 1& 0\\ P& \varphi & 1-\varphi \end{array}$
$x|y=1\sim N({\mu }_1,\Sigma )$
$x|y=0\sim N({\mu }_2,\Sigma )$
$C_1=\{x_i|y_i=1,i=1,...n\}$
$C_2=\{x_i|y_i=0,i=1,...n\}$
$|C_1|=n_1，|C_2|=n_2，则n_1+n_2=n$

即满足条件:
$P(Y)={\varphi }^y(1-\varphi {)}^{1-y},P(X|Y)=N({\mu }_1,\Sigma {)}^{y}N({\mu }_2,\Sigma {)}^{1-y}$

由$P(y|x)\propto P(x|y)P(y)$

那么log-likelihood:
$$\begin{gathered} \hat{\theta }=arg\underset{\theta }{\max }L(\theta ),其中\theta =(\varphi ,{\mu }_1,{\mu }_2,\Sigma ) \\ \begin{array}{rl}L(\theta )& =log\stackrel{n}{\prod _{i=1}}P(y_i|x_i)\\ & =\stackrel{n}{\sum _{i=1}}[logP(x_i|y_i)+logP(y_i)]\\ & =\stackrel{n}{\sum _{i=1}}[logN({\mu }_1,\Sigma {)}^{y_i}N({\mu }_2,\Sigma {)}^{1-y_i}+log{\varphi }^{y_i}(1-\varphi {)}^{1-y_i}]\\ & =\stackrel{n}{\sum _{i=1}}[\underset{①}{\underline{y_{i}logN({\mu }_1,\Sigma )}}+\underset{②}{\underline{(1-y_i)logN({\mu }_2,\Sigma )}}+\underset{③}{\underline{y_{i}log\varphi +(1-y_i)log(1-\varphi )}}]\end{array} \end{gathered}$$

1. 求参数$\varphi$
   只需考虑③，$\hat{\varphi }=arg\underset{\varphi }{\max }③$
   $$\begin{gathered} \frac{\partial L(\theta )}{\partial \varphi }=\stackrel{n}{\sum _{i=1}}[\frac{y_i}{\varphi }-\frac{1-y_i}{1-\varphi }]=0 \\ \begin{array}{rl}& \stackrel{n}{\sum _{i=1}}[y_i(1-\varphi )-\varphi (1-y_i)]=0\\ & \stackrel{n}{\sum _{i=1}}[y_i-y_i\varphi -\varphi +y_i\varphi ]=0\\ & \stackrel{n}{\sum _{i=1}}[y_i-\varphi ]=0\\ & \varphi =\frac{1}{n}\stackrel{n}{\sum _{i=1}}{y}_i=\frac{n_1}{n}\end{array} \end{gathered}$$
2. 求参数$\mu$
   对${\mu }_1$:
   只需考虑①，$\widehat{{\mu }_1}=arg\underset{{\mu }_1}{\max }①$
   多维正态分布：
   $$N(\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\}$$
   对于①：
   $$\begin{array}{rl}①& =\stackrel{n}{\sum _{i=1}}{y}_{i}logN({\mu }_1,\Sigma )\\ & =\stackrel{n}{\sum _{i=1}}[y_{i}log\underline{\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}}exp\{-\frac{1}{2}(x_i-{\mu }_1{)}^T{\Sigma }^{-1}(x_i-{\mu }_1)\}]\\ & \Downarrow \text{系数不影响}\\ 令△& =\stackrel{n}{\sum _{i=1}}[y_i(-\frac{1}{2}(x_i-{\mu }_1{)}^T{\Sigma }^{-1}(x_i-{\mu }_1)]\\ & =-\frac{1}{2}\stackrel{n}{\sum _{i=1}}[y_i(x_i^T{\Sigma }^{-1}{x}_i-\underset{互为转置，乘积为标量可合并}{\underline{x_i^T{\Sigma }^{-1}{\mu }_1-{\mu }_1^T{\Sigma }^{-1}{x}_i}}+{\mu }_1^T{\Sigma }^{-1}{\mu }_1)]\\ & =-\frac{1}{2}\stackrel{n}{\sum _{i=1}}[y_i(\underset{常数}{x_i^T{\Sigma }^{-1}{x}_i}-2{\mu }_1^T{\Sigma }^{-1}{x}_i+{\mu }_1^T{\Sigma }^{-1}{\mu }_1)]\end{array}$$
   对$△求导$
   $$\begin{array}{rl}\frac{\partial △}{\partial {\mu }_1}& =-\frac{1}{2}\stackrel{n}{\sum _{i=1}}[y_i(-2{\Sigma }^{-1}{x}_i+2{\Sigma }^{-1}{\mu }_1)]=0\\ & \stackrel{n}{\sum _{i=1}}[y_i({\Sigma }^{-1}{\mu }_1-{\Sigma }^{-1}{x}_i)]=0\\ & \stackrel{n}{\sum _{i=1}}[y_i{\mu }_1-y_i{x}_i]=0\\ & {\mu }_1=\frac{\stackrel{n}{\sum _{i=1}}{y}_i{x}_i}{\stackrel{n}{\sum _{i=1}}{y}_i}=\frac{\stackrel{n}{\sum _{i=1}}{y}_i{x}_i}{n_1}\end{array}$$
   同理可得
   $${\mu }_2=\frac{\stackrel{n}{\sum _{i=1}}(1-y_i)x_i}{n_2}$$
3. 求参数$\Sigma$
   需同时考虑①②，即$\hat{\Sigma }=arg\underset{{\mu }_1}{\max }①+②$
   为把$y_i$去掉，分别考虑$C_1,C_2$对应集合的情况即可
   $$①+②=\sum _{x_i\in C_1}logN({\mu }_1,\Sigma )+\sum _{x_i\in C_2}logN({\mu }_2,\Sigma )$$
   $$\begin{array}{rl}\stackrel{n}{\sum _{i=1}}logN(\mu ,\Sigma )& =\stackrel{n}{\sum _{i=1}}log\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\{-\frac{1}{2}(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )\}\\ & =\underset{常数}{\underline{-\frac{p}{2}\stackrel{n}{\sum _{i=1}}log2\pi }}-\frac{1}{2}\stackrel{n}{\sum _{i=1}}log|\Sigma |-\frac{1}{2}\stackrel{n}{\sum _{i=1}}(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )\\ & =C-\frac{1}{2}nlog|\Sigma |-\frac{1}{2}\stackrel{n}{\sum _{i=1}}(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )\end{array}$$
   其中$(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )$结果是标量，且有以下公式：
   $$\begin{array}{rl}& tr(a)=a，a是标量\\ & \frac{\partial tr(AB)}{\partial A}=B^T\\ & \frac{\partial |A|}{\partial A}=|A|A^{-1}\\ tr(AB)=tr(BA)& \Rightarrow tr(ABC)=tr(CAB)=tr(BCA)\end{array}$$
   因此：
   $$\begin{array}{rlr}& \stackrel{n}{\sum _{i=1}}(x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu )& \\ & =\stackrel{n}{\sum _{i=1}}tr((x_i-\mu {)}^T{\Sigma }^{-1}(x_i-\mu ))\text{根据（1）}& \\ & =\stackrel{n}{\sum _{i=1}}tr((x_i-\mu {)}^T(x_i-\mu ){\Sigma }^{-1})\text{根据（4）}& \\ & =tr(\underset{样本方差S=\frac{1}{n}\stackrel{n}{\sum _{i=1}}(x_i-\mu {)}^T(x_i-\mu )}{\underline{\stackrel{n}{\sum _{i=1}}(x_i-\mu {)}^T(x_i-\mu )}}{\Sigma }^{-1})& \\ & =tr(nS{\Sigma }^{-1})& =ntr(S{\Sigma }^{-1})\end{array}$$
   原式：
   $$\stackrel{n}{\sum _{i=1}}logN(\mu ,\Sigma )=-\frac{1}{2}nlog|\Sigma |-\frac{1}{2}ntr(S{\Sigma }^{-1})+C$$
   $$\begin{array}{rl}①+②& =-\frac{1}{2}{n}_{1}log|\Sigma |-\frac{1}{2}{n}_{1}tr(S_1{\Sigma }^{-1})-\frac{1}{2}{n}_{2}log|\Sigma |-\frac{1}{2}{n}_{2}tr(S_2{\Sigma }^{-1})+C\\ & =-\frac{1}{2}(\underset{(3)}{\underline{nlog|\Sigma |}}+\underset{(2)，S对称，S^T=S}{\underline{n_{1}tr(S_1{\Sigma }^{-1})+n_{2}tr(S_2{\Sigma }^{-1})}})+C\end{array}$$
   求导：
   $$\begin{array}{rl}\frac{\partial ①+②}{\partial \Sigma }& =-\frac{1}{2}(n\frac{1}{|\Sigma |}|\Sigma |{\Sigma }^{-1}-n_1{S}_1^T{\Sigma }^{-2}-n_2{S}_2^T{\Sigma }^{-2})\\ & =-\frac{1}{2}(n{\Sigma }^{-1}-n_1{S}_1{\Sigma }^{-2}-n_2{S}_2{\Sigma }^{-2})=0\\ & n\Sigma -n_1{S}_1-n_2{S}_2=0\\ & \hat{\Sigma }=\frac{1}{n}(n_1{S}_1+n_2{S}_2)\end{array}$$

2.2.2 Naive Bayes

思想：
条件独立性假设（每个属性之间相互独立）
目的是简化运算
$$\begin{gathered} \hat{y}=arg\underset{y}{\max }P(y|x)=arg\underset{y}{\max }P(x|y)P(y) \\ P(x|y)=\stackrel{p}{\prod _{j=1}}P(x_j|y),这里x_j是属性 \end{gathered}$$