数字图像处理考点分析（二）
上一篇：数字图像处理考点分析（一） 我们介绍了数字图像处理的一些基础知识，现在我们就要正式开始对数字图像进行处理了！
图像增强
文章目录
-
-
- 图像增强
-
- 空间域图像增强
-
- 灰度变换
-
- 直方图
- 直方图均衡化
- 直方图规定化（匹配）
- 空间滤波
-
- 平滑空间滤波器
- 锐化空间滤波器
-
Q:图像增强是什么？
不考虑 图像降质的原因，只将图像中感兴趣的特征有选择地突出，对不需要的特征进行衰减。
Q:为什么要进行图像增强？
图像增强的目的：①改善图像视觉效果，便于观察和分析；②便于人工或机器对图像的进一步处理
Q:怎样进行图像增强？
由上图，我们知道图像增强有两种处理方法，分别是空间域增强和频域增强。
空间域增强是对图像的像素直接处理
频域增强是修改图像的傅里叶变换
首先，我们来看看如何利用空域方法进行图像增强！
空间域图像增强
空间域的图像增强又可以分为灰度变换（点处理）和空间滤波（模板处理）两种方法
灰度变换
对图像的单个像素进行操作，主要以对比度和阈值处理为目的
对图像在空间域的处理公式可表示为：
g(x,y) = T[f(x,y)]
其中，f(x,y)是输入图像，g(x,y)是处理后的图像，T是在点(x,y)对邻域上定义的关于f的一种算子。算子可应用于单幅图像或图像集合。
若用r和s分别表示f和g在任一点(x,y)处的灰度，则灰度变换函数可表示为：
s = T（r）
灰度变换的关键：根据要解决的图像增强问题，选择合适的灰度变换函数T（r）。
Q:有哪些灰度变换函数？
-
反转变换
s = L - 1 - r [0,L-1]为图像的灰度级。作用：黑的变白，白的变黑经此处理，可得到等效的照片底片。
此类处理适用于增强嵌入图像暗色区域中的白色或灰色细节，特别是当黑色面积在尺寸上占主导地位时。 -
对数变换
s =clog(1+ r) 其中c为常数，假设r>=0对数变换是将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值，或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。扩展图像中的暗像素值，同时压缩更高灰度级的值。
应用：有时原图的动态范围太大，超出某些显示设备的允许 动态范围，如直接使用原图，则一部分细节可能丢失，解决办法是对原图进行灰度级压缩，如对数变换
-
幂次（伽马）变换
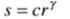
其中c和γ为正常数
- γ<1时，γ越小，该变换越将低灰度值（暗值）进行拉伸
- γ>1时，γ越大，该变换越将高灰度值（亮值）进行拉伸
应用：主要用于图像的校正，将漂白的图片或是过黑的图片，进行修正。
-
分段线性变换
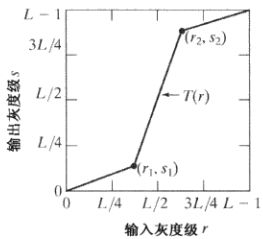
对比度拉伸
对比度拉伸是扩展图像灰度级动态范围的处理。通过调整折线拐点的位置 及控制分段直线的斜率，可对任一灰度区间进行拉伸或压缩
点（r1,s1）和点（r2,s2）的位置控制变换函数的形状。一般情况下，假设r1<=r2，s1<=s2，保证函数是单值的且是单调递增的。
灰度级分层
突出图像中特定灰度范围的亮度。
左图：突出目标的轮廓，消除背景细节
右图：突出目标的轮廓，保留背景细节位平面分层
像素是由比特组成的数字。如，256级灰度图像中，每个像素由8比特组成。假设图像是由8个1位平面组成，范围从位平面0 到位平面7。其中，位平面0包含图像中像素的最低位，位平 面7包含像素的最高位。 通过对特定位提高亮度，改善图像质量。
高阶比特包含了在视觉上很重要的大多数数据。低阶比特平面在图像中贡献了更精细的灰度细节。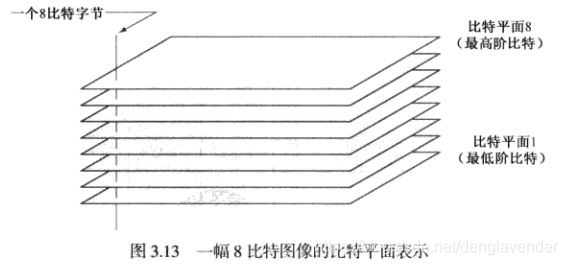
直方图
直方图运算
先简单介绍下图像的直方图：
直方图统计一幅图像中各个灰度级出现的次数
直方图反映的是图像灰度级的统计信息，但丢失了所有像素点的空间信息，即像素点的相对位置
任意特定的图像有唯一的直方图，但反之不成立。
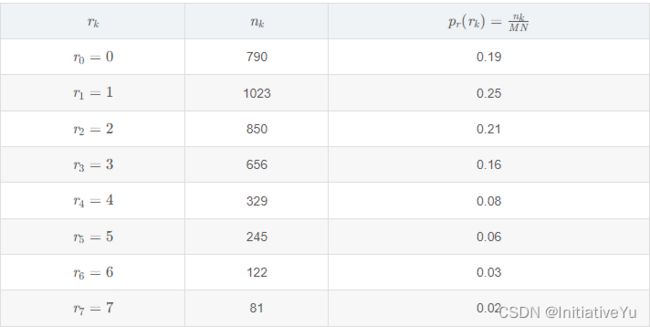
一个灰度级在范围[0，L-1]的数字图像的直方图 是一个离散函数：
其中M*N是图像的像素总数，nk是图像中灰度级为rk 的像素个数；rk是第k个灰度级，k = 0, 1, 2,…,L-1。
上述定义的特点：
-
使函数值正则化到[0,1]区间，成为实数函数；
-
函数值的范围与像素的总数无关；
-
给出灰度级rk在图像中出现的概率密度统计。
直方图均衡化
将原图像的直方图通过变换函数变为均匀的直方图，然后按均匀直方图修改原图像，从而获得一幅灰度分布均匀的新图像。
目的：增加灰度值的动态范围，增强图像的对比度。
s=T（r） 0≤r≤1
T（r）满足下列两个条件：
（1）T（r）在区间0≤r≤1中为单值且单调递增
（2）当0≤r≤1时,0≤T（r）≤1
条件（1）保证原图各灰度级在变换后仍保持从黑到白 （或从白到黑）的排列次序。
条件（2）保证变换前后灰度级范围的一致性
**基本思想：**对在图像中像素个数多的灰度级进行展宽， 而对像素个数少的灰度级进行缩减合并，从而达 到增加对比度，提升图像清晰度的目的。
均衡化的具体步骤(五步法)
-
求灰度直方图
统计表格中的灰度值及其出现的次数
-
计算灰度分布概率
灰度分布概率=各灰度值像素的个数/像素总数
-
计算灰度级从小到大的累积分布
-
将归一化的hp（上一步求得的累积分布）乘以 L-1 再四舍五入，以使得均衡化后图像的灰度级与归一化前的原始图像一致。
举例：原图像灰度值为1的累积分布为0.20，L为10(原图像又有10个灰度级)，则0.20*（10-1）=1.8，再四舍五入为2，则新图像对应的灰度级为2
-
根据以上映射关系，参照原始图像中的像素，可以写出直方图均衡化之后的图像
直方图均衡化后，得到的新图像的特点：
-
灰度级减少，出现 “简并”现象。对比度增加，图像 更清晰。
-
动态范围增大，直方图更平坦。适用于对比度较弱或灰度集中的图像。
直方图规定化（匹配）
直方图规定化是将原始图像的直方图转换为期望（特定）的直方图的形状。是以直方图均衡化变换为中介来实现的。
具体步骤如下：
- 将原始图像的灰度直方图进行均衡化，得到一个变换函数s=T®，其中s是均衡化后的像素，r是原始像素
- 对规定的直方图进行均衡化，得到一个变换函数v=G(z)，其中v是均衡化后的像素，z是规定化的像素
- 上面都是对同一图像的均衡化，其结果应该是相等的,s=v,且z=G−1(v)=G−1(T®)
通过，均衡化作为中间结果，将得到原始像素r和z规定化后像素之间的映射关系。
示例：
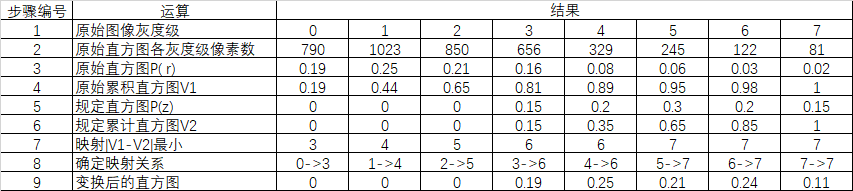
对一幅大小为64×64像素（MN=4096)的3比特图像(L=8)的灰度分布如下表所示：
确定映射关系执行直方图规定化的过程如下：
关于第七步：V1–>v2的映射
举例：如灰度级0的原始累计直方图V1值为0.19，它最接近的规定累积直方图V2中灰度级为3对应的值(0.15) 则第七步中原始图像灰度级0所对应的值为3
直方图规定化可以这么理解：输入图A具有直方图ZA，输入图B具有直方图ZB，为了让图A具有类似ZB的直方图，选择使用直方图均衡进行过渡，对A进行直方图均衡得到结果PA，PA具有1(L-1)的分布，对B进行直方图均衡得到结果PB，PB具有1(L-1)的分布，此时，将PA的像素与PB的像素一一对应，就能得到结果图像
在实际开发过程中，可以按如下思路执行：
1 计算输入图像的灰度直方图，并求得该直方图对应的累积概率分布图；
2 计算规定目标图像的灰度直方图，并求得该直方图对应的累积概率分布图；
3 将输入图像的累积概率分布图中的各个值，在规定目标图像的累积概率分布图上查找与之最接近的值，并将该值对应的灰度级与输入图像的各个值行成查找表。
4 对输入图像执行查表操作。
--------------下面开始介绍空域增强的另一种方案==>空间滤波-------------
空间滤波
Q:空间滤波是什么？
使用空间模板进行的图像处理，被称 为空间滤波。模板本身被称为空间滤波器。
空间滤波需要对原始图像中的每个像素(x,y)都进 行处理，才能得到滤波后的图像。
空间滤波的步骤
步骤：（空间滤波都是利用模板卷积，下述的模板即是滤波器）
1、将模板在图中漫游，并将模板中心与图中某个像素位置重合；
2、将模板上系数与模板下对应像素相乘
3、将所有乘积相加（为保持灰度范围，常将结果再除以模板中所有系数的和）
4、将和（模板的输出响度）赋给图中对应模板中心位置的像素。
当模板边界超出图像的边界时，注意边界问题的处理，最常用的方法时填充，但其会影响图像的边界，影响程度随模板尺寸的增大而增加。
ps.滤波器的尺寸一般都是奇数尺寸，最小尺寸为3*3。
平滑空间滤波器
用于模糊处理和降低噪声，淡化细节部分。
通过线性滤波和非线性滤波的处理，可以降低噪声。
缺点：如果图像处理的目的是去除噪音，那么在去除噪音的同时也钝化了图像的边和尖锐的细节。
平滑空间滤波器的分类
-
线性滤波器：均值滤波器
思想：使用滤波器模板确定的邻域内的像素的平均灰度值代替图像中的每个像素。
分类：- 盒状滤波器：所有系数都相等的空间均值滤波器
- 加权均值滤波器：赋予中心点最高权重，然后随着距中心点距离的增加而减少系数的加权策略的目的，是在平滑处理中试图降低模糊。
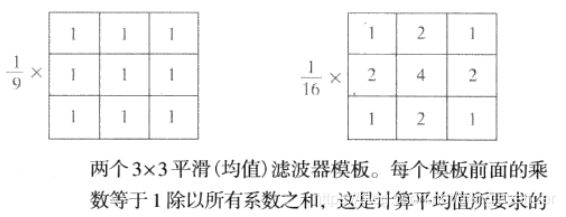
作用： 减小噪声的同时，也减小图像灰度的“尖锐”变化。
由于图像边缘是由图像灰度尖锐变化引起的，所 以也存在边缘模糊的问题。
-
非线性滤波器：统计排序滤波器
思想： 基于滤波器所在图像区域中像素的排序，由排序 结果决定的值代替中心像素的值。
分类：
-
中值滤波器： 用像素领域内的中间值代替该像素 用途：去除噪声(有效去除椒盐噪声)
ps.在去除噪声的同时，可以比较好地保留边的锐度和图像的细节（优于均值滤波器）；
-
最大值滤波器：用像素领域内的最大值代替该像素 用途：寻找最亮点
-
最小值滤波器：用像素领域内的最小值代替该像素 用途：寻找最暗点
-
锐化空间滤波器
Q:锐化空间滤波器用来做什么？
-
用于突出灰度的过渡部分，突出细节或者增强被模糊了的细节
-
图像识别中，分割前的边缘提取；
-
锐化处理恢复过度钝化、暴光不足的图像；
Q:锐化空间滤波器的分类?
-
二阶微分滤波器－拉普拉斯算子
各向同性滤波器：旋转不变，即将原图像旋转后进行滤波处理给出的结果，与先对图像滤波后再旋转的结果相同。
拉普拉斯算子：最简单的各向同性微分算子。
二维图像函数f(x,y)的拉普拉斯算子定义如下：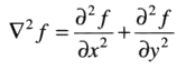
任意阶的微分都是线性操作，故拉普拉斯变换也是一个线性算子。
两个变量的离散拉普拉斯算子：
拉普拉斯的应用着重于图像中的灰度突变区域，而非灰度级缓慢变换的区域。拉普拉斯图像增强是要将原图像和拉普拉斯图像进行叠加（相加或相减）来得到最终的结果。
使用拉普拉斯图像增强的基本方法：
所定义的中心系数是负的，则c = -1，反之，c = 1
-
一阶微分滤波器－梯度算子
在某些实现中，用绝对值类近似向量模值的计算：
有以下分类：
Roberts交叉梯度算子
Prewitt梯度算子
Sobel梯度算子
好了，空域增强就介绍到这里。
下一篇，我们将介绍图像增强的另一种实现——频域增强 数字图像处理考点分析（三）