文章综述——SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
一、代码
1.代码下载：https://github.com/tkipf/pygcn
代码运行方式：
1）cmd安装：python setup.py install（作用是作者Thomas Kipf已经将写好图卷积网络gcn做成了安装包，安装在python目录下的lib）
2）cmd运行：python train.py
注
- PyTorch 0.4 or 0.5
- Python 2.7 or 3.6
代码运行结果：
2.代码详解
1）train.py
固定参数设置：epoch，学习率，dropout，隐藏层数，权重衰减（weight decay），随机数 Random seed
L2正则化的目的就是为了让权重衰减到更小的值，在一定程度上减少模型过拟合的问题，所以权重衰减也叫L2正则化
model——GCN：特征数，隐藏层数，分类数=标签数+1，dropout数
optimizer（优化）——Adam一般来说是收敛最快的优化器，所以被用的更为频繁
model.train()与model.eval()的用法
接触pytorch时套用别人的框架，会在训练开始之前写上model.trian()，在测试时写上model.eval()。
在经过一番查阅之后，总结如下：
如果模型中有BN层(Batch Normalization）和Dropout，需要在训练时添加model.train()，在测试时添加model.eval()。其中model.train()是保证BN层用每一批数据的均值和方差，而model.eval()是保证BN用全部训练数据的均值和方差；而对于Dropout，model.train()是随机取一部分网络连接来训练更新参数，而model.eval()是利用到了所有网络连接。
2）model.py
- nfeat,底层节点的参数，feature的个数
- nhid，隐层节点个数
- nclass，最终的分类数
- dropout
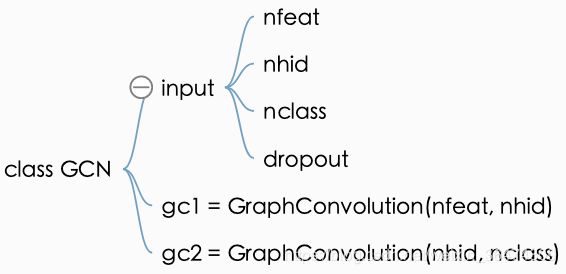
网络结构（核心）
结合论文，此公式为：
- 隐层的feature maps的数量为H，输入层数量为C，输出层为F
- 其中A为下面3.4中提到的对称邻接矩阵symmetric adjacency matrix，
- 权重
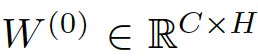为输入层到隐层的权值矩阵 - 同理，权重
为隐层到输出层的权值矩阵 - 这个公式跟BP有点像，只不过比BP多了一个稀疏的邻接矩阵 A
代码流程（依据上述公式，gc是图卷积层）：
- gc1后接一个relu激活
- x进行dropout
- 然后x与adj通过gc2
- 通过softmax回归得到最终的输出
3）layers.py（gc函数封装）
a.图卷积层初始化定义：
输入feature，输出feature，权重，偏移。
b.初始化权重（初始化为均匀分布）：
c.前馈运算
如以下公式中的矩阵相乘：
- 直接输入与权重之间进行torch.mm操作，得到support，即XW
- support与adj进行torch.spmm操作，得到output，即AXW
- 选择是否加bias
torch.mul(a, b)是矩阵a和b对应位相乘，a和b的维度必须相等，比如a的维度是(1, 2)，b的维度是(1, 2)，返回的仍是(1, 2)的矩阵torch.mm(a, b)是矩阵a和b矩阵相乘，比如a的维度是(1, 2)，b的维度是(2, 3)，返回的就是(1, 3)的矩阵- torch.spmm(a,b)稀疏矩阵乘法
3.数据结构（用于论文类型分类） 具体代码：utils.py
data文件夹里有Cora数据：content file 和 cites file（用记事本打开即可）
1）content file
列类型：
注：第一列为paper ID，后面几列为每个单词出现与否，用0与1表示，最后一列为类别标签。
代码读取：
idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
dtype=np.dtype(str))
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
labels = encode_onehot(idx_features_labels[:, -1])
feature为第二列到倒数第二列，labels为最后一列
2）cites file
表示论文之间的引用关系（可想象为拓扑图的连接关系，有向图）
前面为被引论文的ID，后面为引用前面的论文的ID
代码：（根据前面的contents与这里的cites创建图，算出edges矩阵与adj 矩阵。）
# build graph
idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
idx_map = {j: i for i, j in enumerate(idx)}
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
dtype=np.int32)
edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
dtype=np.int32).reshape(edges_unordered.shape)
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
shape=(labels.shape[0], labels.shape[0]),
dtype=np.float32)矩阵的定义如下：
3）Python将非对称邻接矩阵转变为对称邻接矩阵symmetric adjacency matrix(有向图转无向图)
# build symmetric adjacency matrix
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
# 正则化矩阵
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))
矩阵转化实例：https://blog.csdn.net/iamjingong/article/details/97392571
coo_matrix函数：https://www.cnblogs.com/datasnail/p/11021835.html
邻接矩阵：https://baike.baidu.com/item/%E9%82%BB%E6%8E%A5%E7%9F%A9%E9%98%B5/9796080?fr=aladdin#1
4）数据集分割
分割为train，val，test三个集
最终数据加载为torch的格式
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)
idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)
二、文章摘要：
提出了一种可扩展的在图结构数据上进行半监督学习的方法，它基于一种直接在图上操作的卷积神经网络的有效变体。我们通过频谱图卷积的局部一阶近似来激励卷积架构的选择。我们的模型以图形边的数量线性缩放，并学习编码局部图结构和节点特征的隐藏层表示。在一些引用网络和知识图数据集的实验中，我们证明了我们的方法有显著性作用
正文：
我们考虑了对图(如引用网络)中的节点(如文档)进行分类的问题，其中标签只对一小部分节点可用。这个问题可以被框定为基于图的半监督学习，通过某种形式的显式基于图的正则化来平滑图上的标签信息，例如在损失函数中使用图Laplacian正则化项:Eq. 1的公式是基于图中连接节点可能共享同一标签的假设。然而，这种假设可能会限制建模能力，因为图的边缘不一定需要编码节点相似性，但可能包含额外的信息。
在本工作中，我们直接使用神经网络模型f(X, a)对图结构进行编码，并对所有带标签的节点进行监督目标L0的训练，从而避免了损失函数中基于图的显式正则化。对图的邻接矩阵f(·)进行条件设置将允许模型从监督损失L0中分配梯度信息，并使其能够学习带标签和不带标签的节点表示。
我们贡献是双重的。首先，我们为神经网络模型引入了一个简单的、表现良好的分层传播规则，该规则直接对图进行操作，并展示了如何从频谱图卷积的一阶近似中激发该规则
其次，我们演示了这种基于图的神经网络模型如何用于快速和可扩展的图中节点的半监督分类。在大量数据集上的实验表明，我们的模型在分类精度和效率方面都是比较好的