【深度学习基础】BatchNorm,LayerNorm,InstanceNorm,GroupNorm 和 WeightNorm 的原理与PyTorch逐行实现
都参考了讲解视频,感谢分享!!!!
(我的理解不到位,存在纰漏,请指出!)
1. 整理
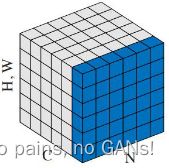
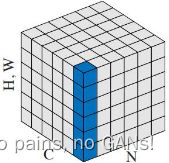
表中,N 为批量大小,C 是通道数,H/W 是长宽,L 是序列长度,G 是分组的数量。
1.1 为什么 NLP 中用 LayerNorm,而不是 BatchNorm?
最关键原因就是:在时序模型中,每个样本的长度可能会发生变化, L a y e r N o r m LayerNorm LayerNorm 按照每个样本来计算均值和方差,同时也不需要存下一个全局的均值和方差,这样的话更稳定一些。而 BatchNorm 就会忽略样本长度的问题。
2. 动手实现
2.1 BatchNorm2d
import torch
import torch.nn as nn
# 在 CV 中测试 BatchNorm2d
batch_size = 2
channels = 2
H = W = 4
input_x = torch.randn(batch_size, channels, H, W) # N * C * H * W
# 官方 API 结果
batch_norm_op = torch.nn.BatchNorm2d(num_features=channels, affine=False) # 方便验证,关闭了 affine
bn_y = batch_norm_op(input_x)
# 手写 batch_norm
bn_mean = input_x.mean(dim=(0, 2, 3)).unsqueeze(0).unsqueeze(2).unsqueeze(3).repeat(batch_size, 1, H, W) # 在除了通道维度以外的其他维度计算均值,也就是最后是每个通道的均值
bn_var = input_x.var(dim=(0, 2, 3), unbiased=False, keepdim=True) # 用有偏估计算标准差,上面也可以用 keepdim=True 只是这里展示了两种不同写法
verify_bn_y = (input_x - bn_mean)/torch.sqrt((bn_var + 1e-5))
print(bn_y)
print(verify_bn_y)
2.2 LayerNorm
import torch
import torch.nn as nn
# 在 NLP 中测试 LayerNorm
batch_size = 2
time_steps = 3
embedding_dim = 4
input_x = torch.randn(batch_size, time_steps, embedding_dim) # N * L * C
# 官方 API 结果
Layer_norm_op = torch.nn.LayerNorm(normalized_shape=embedding_dim, elementwise_affine=False)
ln_y = Layer_norm_op(input_x)
# 手写 Layer_norm
ln_mean = input_x.mean(dim=-1, keepdim=True) # 对每个样本求均值和方差
ln_var = input_x.var(dim=-1, keepdim=True, unbiased=False) # 用有偏估计算标准差
verify_ln_y = (input_x - ln_mean) / torch.sqrt((ln_var + 1e-5))
print(ln_y)
print(verify_ln_y)
#-------------------------------------------#
# 在 CV 中测试 LayerNorm
batch_size = 2
channels = 2
H = W = 4
input_x = torch.randn(batch_size, channels, H, W) # N * C * H * W
# 官方 API 结果
Layer_norm_op = torch.nn.LayerNorm(normalized_shape=[channels, H, W], elementwise_affine=False)
ln_y = Layer_norm_op(input_x)
# 手写 batch_norm
ln_mean = input_x.mean(dim=(1, 2, 3), keepdim=True) # 计算均值
ln_var = input_x.var(dim=(1, 2, 3), keepdim=True, unbiased=False) # 用有偏估计算标准差,上面也可以用 keepdim=True 只是这里展示了两种不同写法
verify_ln_y = (input_x - ln_mean) / torch.sqrt((ln_var + 1e-5))
print(ln_y)
print(verify_ln_y)
2.3 InstanceNorm2d
import torch
import torch.nn as nn
# 在 CV 中测试 InstanceNorm2d
batch_size = 2
channels = 2
H = W = 4
input_x = torch.randn(batch_size, channels, H, W) # N * C * H * W
# 官方 API 结果
in_norm_op = nn.InstanceNorm2d(num_features=channels) # affine 已经默认为 False
in_y = in_norm_op(input_x)
# 手写 instance_norm
in_mean = input_x.mean(dim=(2, 3), keepdim=True) # 沿特征图计算均值
in_var = input_x.var(dim=(2, 3), keepdim=True, unbiased=False) # 用有偏估计算标准差
verify_in_y = (input_x - in_mean) / torch.sqrt((in_var + 1e-5))
print(in_y)
print(verify_in_y)
2.4 GroupNorm
# 在 CV 中测试 GroupNorm
groups = 2
batch_size = 2
channels = 2
H = W = 4
input_x = torch.randn(batch_size, channels, H, W) # N * C * H * W
# 官方 API 结果
gn_op = nn.GroupNorm(num_groups=groups, num_channels=channels, affine=False)
gn_y = gn_op(input_x)
# 手写 instance_norm
group_input_xs = torch.split(input_x, split_size_or_sections=channels//groups, dim=1)
results = []
for group_input_x in group_input_xs:
gn_mean = group_input_x.mean(dim=(1, 2, 3), keepdim=True) # 每个样本每一组计算均值
gn_var = group_input_x.var(dim=(1, 2, 3), keepdim=True, unbiased=False) # 用有偏估计算标准差
gn_result = (group_input_x - gn_mean) / torch.sqrt((gn_var + 1e-5))
results.append(gn_result)
verify_gn_y = torch.cat(results, dim=1)
print(gn_y)
print(verify_gn_y)
2.5 weight_norm
import torch
import torch.nn as nn
# 测试 weight_norm
batch_size = 2
n = 4
input_x = torch.randn(batch_size, n) # 2 * 4
linear = nn.Linear(n, 3, bias=False)
# 官方 API 结果
wn_linear = nn.utils.weight_norm(module=linear, name='weight', dim=0)
wn_y = wn_linear(input_x) # 2 * 3
# 手写 batch_norm
weight_direction = linear.weight / (linear.weight.norm(dim=1, keepdim=True)) # 3 * 4
weight_magnitude = torch.tensor([linear.weight[i, :].norm() for i in torch.arange(linear.weight.shape[0])],
dtype=torch.float32).unsqueeze(-1) # 3 * 1
verify_wn_y = input_x @ (weight_direction.transpose(-1, -2)) * (weight_magnitude.transpose(-1, -2))
print(wn_y)
print(verify_wn_y)
```2.5 weight_norm
```python
import torch
import torch.nn as nn
# 测试 weight_norm
batch_size = 2
n = 4
input_x = torch.randn(batch_size, n) # 2 * 4
linear = nn.Linear(n, 3, bias=False)
# 官方 API 结果
wn_linear = nn.utils.weight_norm(module=linear, name='weight', dim=0)
wn_y = wn_linear(input_x) # 2 * 3
# 手写 batch_norm
weight_direction = linear.weight / (linear.weight.norm(dim=1, keepdim=True)) # 3 * 4
weight_magnitude = wn_linear.weight_g # 3 * 1
verify_wn_y = input_x @ (weight_direction.transpose(-1, -2)) * (weight_magnitude.transpose(-1, -2))
print(wn_y)
print(verify_wn_y)