svd分解
sklearn中svd分解
class sklearn.decomposition.TruncatedSVD(n_components=2, *, algorithm='randomized', n_iter=5, random_state=None, tol=0.0)参数:
n_components:整数,默认=2
输出数据的所需维度。必须严格小于特征数。默认值对可视化很有用。对于 LSA,建议值为 100。
algorithm:{‘arpack’, ‘randomized’},默认='随机'
要使用的 SVD 求解器。 “arpack” 用于 SciPy (scipy.sparse.linalg.svds) 中的 ARPACK 包装器,或 “randomized” 用于 Halko (2009) 中的随机算法。
n_iter:整数,默认=5
随机 SVD 求解器的迭代次数。 ARPACK 不使用。默认值大于 randomized_svd 中的默认值,以处理可能具有大的缓慢衰减频谱的稀疏矩阵。
random_state:int,RandomState 实例或无,默认=无
在随机 svd 期间使用。传递一个 int 以获得跨多个函数调用的可重现结果。请参阅词汇表。
tol:浮点数,默认=0.0
ARPACK 的容差。 0 表示机器精度。被随机 SVD 求解器忽略。
属性:
components_:ndarray 形状(n_components,n_features)
输入数据的右奇异向量。
explained_variance_:ndarray 形状 (n_components,)
通过投影变换到每个分量的训练样本的方差。
explained_variance_ratio_:ndarray 形状 (n_components,)
每个选定组件解释的方差百分比。
singular_values_:ndarray od 形状(n_components,)
对应于每个选定组件的奇异值。奇异值等于 lower-dimensional 空间中
n_components变量的 2 范数。n_features_in_:int
拟合期间看到的特征数。
feature_names_in_:ndarray 形状(
n_features_in_,)拟合期间看到的特征名称。仅当
X具有全为字符串的函数名称时才定义。方法
fit(X[, y])
Fit model on training data X.(在训练数据上拟合模型x)
fit_transform(X[, y])
Fit model to X and perform dimensionality reduction on X.
get_feature_names_out([input_features])
Get output feature names for transformation.(获取转换的输出特征名称)
get_params([deep])
Get parameters for this estimator.(获取此估算器的参数)
inverse_transform(X)
Transform X back to its original space.(将X转换回原始空间)
set_params(**params)
Set the parameters of this estimator.
transform(X)
Perform dimensionality reduction on X.
from sklearn.decomposition import TruncatedSVD
from scipy.sparse import csr_matrix
import numpy as np
np.random.seed(0)
X_dense = np.random.rand(10, 10)
X_dense[:, 2 * np.arange(5)] = 0
X = csr_matrix(X_dense)
print('稀疏矩阵\n',X)
#定义svd模型
svd = TruncatedSVD(n_components=3, n_iter=7, random_state=42)
#训练模型
svd.fit(X)
print('所选特征方差百分比',svd.explained_variance_ratio_)
print('方差百分比',svd.explained_variance_ratio_.sum())
print('每个特征的奇异值',svd.singular_values_)
print('模型的参数',svd.get_params(deep=True))
x=np.random.rand(1, 10)
print('之前的数据',x)
print('转换后的数据',svd.transform(x))from sklearn.decomposition import TruncatedSVD
from scipy.sparse import random as r
import numpy as np
# 假设数据是5*10的
x=np.random.randint(1,10,size=[5,10])
# print("原始数据\n",x)
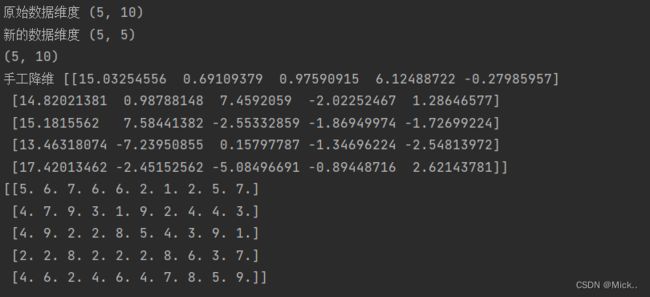
print('原始数据维度',x.shape)
svd=TruncatedSVD(n_components=5)
svd.fit(x)
new_x=svd.transform(x)
print('新的数据维度',new_x.shape)
# 手工降维,right即为svd分解后的右矩阵
right=svd.components_
print(right.shape)
# 计算
print('手工降维',np.dot(x,right[:,:].T))
# sklearn可以直接复原
print(svd.inverse_transform(new_x))
使用numpy进行降维和复原
import numpy as np
# 假设数据是5*10的
x=np.random.randint(1,10,size=[5,10])
# print("原始数据\n",x)
print('原始数据维度',x.shape)
# 可以得到三个矩阵
u,s,v=np.linalg.svd(x)
print("u,s,v的形状:")
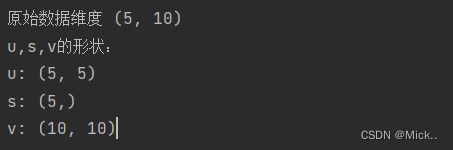
print("u:",u.shape)
print("s:",s.shape)
print("v:",v.shape)
降维,利用x,v实现降维
import numpy as np
# 假设数据是5*10的
x=np.random.randint(1,10,size=[5,10])
# print("原始数据\n",x)
print('原始数据维度',x.shape)
# 可以得到三个矩阵
u,s,v=np.linalg.svd(x)
print("u,s,v的形状:")
print("u:",u.shape)
print("s:",s.shape)
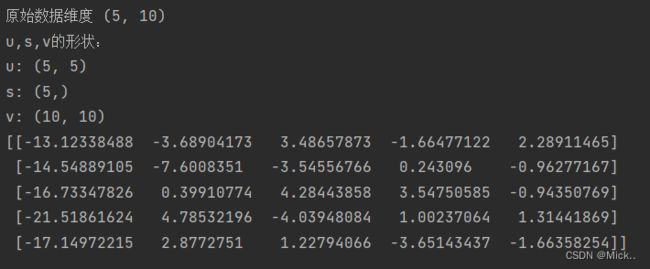
print("v:",v.shape)
# 降维结果与sklearn基本一致,假设降维到n_com=5
print(np.dot(x,v[:5,:].T))
利用u,s,v复原
import numpy as np
# 假设数据是5*10的
x=np.random.randint(1,10,size=[5,10])
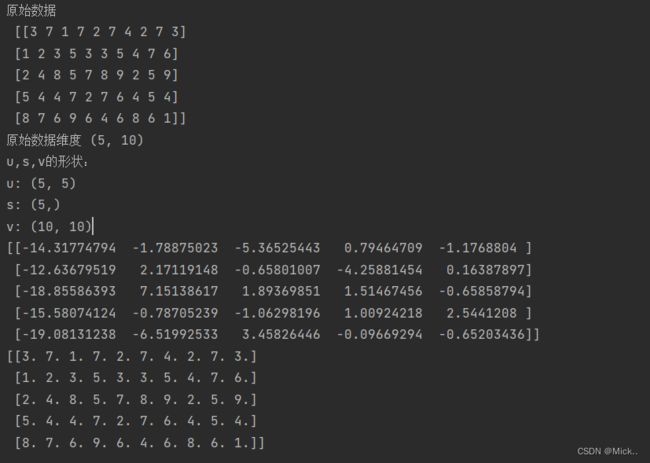
print("原始数据\n",x)
print('原始数据维度',x.shape)
# 可以得到三个矩阵
u,s,v=np.linalg.svd(x)
print("u,s,v的形状:")
print("u:",u.shape)
print("s:",s.shape)
print("v:",v.shape)
# 降维结果与sklearn基本一致,假设降维到n_com=5
print(np.dot(x,v[:5,:].T))
# m为原始行数,n为原始列数
m = 5
n = 10
# 将u、v、s三个矩阵进行运算,将结果累加到a中并返回
a = np.zeros([m, n])
for i in range(0,5):
# 依次取出u和v矩阵的对应数据,并reshape
ui = u[:, i].reshape(m, 1)
vi = v[i].reshape(1, n)
# 将其按照s的权重进行累加
a += s[i] * np.dot(ui, vi)
# 结果与原始数据基本一致
print(a)参考文献
用截断奇异值分解(Truncated SVD)降维_纸上得来终觉浅~的博客-CSDN博客_截断奇异值分解