R与结构方程模型（2）：潜变量

原文链接：https://m-clark.github.io/sem/

并非我们想要衡量的一切都有一个明显的标准。如果一个人想衡量一个人的幸福感，他们会有什么可支配的？

• 他们在微笑吗？
• 他们刚刚得到加薪吗？
• 他们是否与他人互动良好？
• 他们相对健康吗？

其中任何一个都可以作为他们当前幸福状态的指标，但当然，他们都不会告诉我们他们是否真的快乐。充其量它们可以被认为是不完美的措施。如果我们把这些指标和其他指标放在一起考虑，也许我们可以得到一个潜在的衡量标准，我们可以称之为幸福感、满足感或其他一些任意但描述性的名字。

尽管上面对潜在变量的描述与它们在心理学，教育学和相关领域中的通常使用方式一致，但潜在变量模型的使用实际上随处可见，并且可能与我们将在这里主要关注的内容无关。从广义上讲，因子分析可以被视为一种降维技术，或者可以看作是一种对测量误差进行建模和理解潜在结构的方法。我们将对 1前者 进行一些描述，同时重点介绍 2后者 。

降维

在进入SEM上下文中我们称之为测量模型之前，我们可以首先从更一般的角度来看待事物，特别是在降维方面。很多时候，我们只是想获取大量变量，将它们减少到更少，同时保留尽可能多的有关原始变量的信息。例如，这是图像和音频压缩领域非常常见的目标。适合这些方法的统计技术通常被称为 矩阵因式分解。

主成分分析

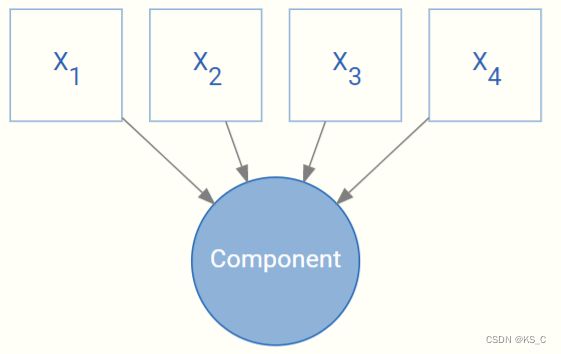
最常用的因子分析技术可能是主成分分析（PCA）。它试图从一组变量中提取 组件，每个组件都包含尽可能多的能够解释原始变异。相同，它可以被看作是在低维子空间上的投影，这些子空间与原始数据的距离最小。组件是原始变量的线性组合。

PCA 通过协方差/相关矩阵进行分析，PCA得到的主成分个数和原始变量数相同。所有 组件的方差依次减少，并且对所有组件求和，将得到100% 的原始数据中的总差异。通过适当的步骤，组件可以完全再现原始数据/相关矩阵。但是，由于目标是降维，我们只想保留其中一些组件，因此再现的矩阵将不精确。然而，这给了我们一些目标感，同样的想法也用于因子分析/ SEM，我们也使用协方差矩阵，并且更喜欢那些更能够精确复现原始数据相关矩阵的模型。

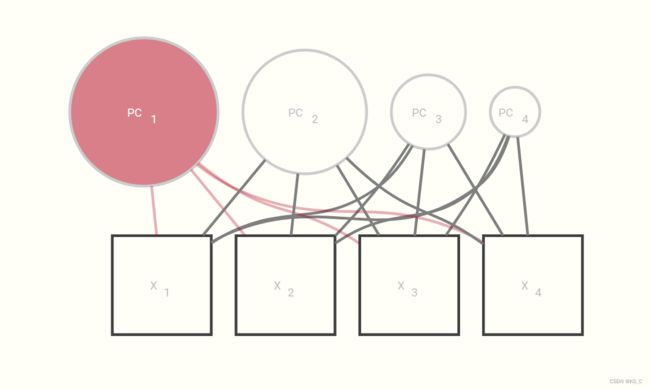
我们可以将PCA显示为如下的图形模型。这是一个有四个组件/变量的。组件的大小表示每个科目的差异量。

让我们看一个示例。下面是关于一个非常小的数据集，来自洛杉矶的12个人口普查区里的5个社会经济指标（哈曼，1967年的经典例子¹）。我们将使用 psych 包，以及其中principal函数。要使用该函数，我们提供了包内的函数，指定我们要保留的组件/因子的数量以及其他选项（ 在这种情况下，旋转解决方案可能更具可解释性，但通常不会在 PCA 中使用，因此我们指定“无” ）。与标准PCA包和功能相比，psych包为我们提供了更多的选择，并且与我们稍后将花时间使用的因子分析技术更加一致。虽然我们也将使用lavaan进行因子分析，以与SEM方法保持一致，但psych包是标准因子分析，评估可靠性（scale reliability）和其他有趣内容的绝佳工具。

对于 PCA，我们将保留三个组件，并且不使用旋转，并且我们还使用标准化数据。如果不这样做，将导致组件偏向于相对于其他变量具有更大方差的变量²。由于这种标准化几乎总是作为PCA的预处理步骤进行，尽管在这里可以选择将其指定为函数的一部分（covar=F³）

library(psych)
pc = principal(Harman.5, nfactors=2,  rotate='none', covar = F)
pc

Principal Components Analysis
Call: principal(r = Harman.5, nfactors = 2, rotate = "none", covar = F)
Standardized loadings (pattern matrix) based upon correlation matrix
                     PC1   PC2   h2    u2   com
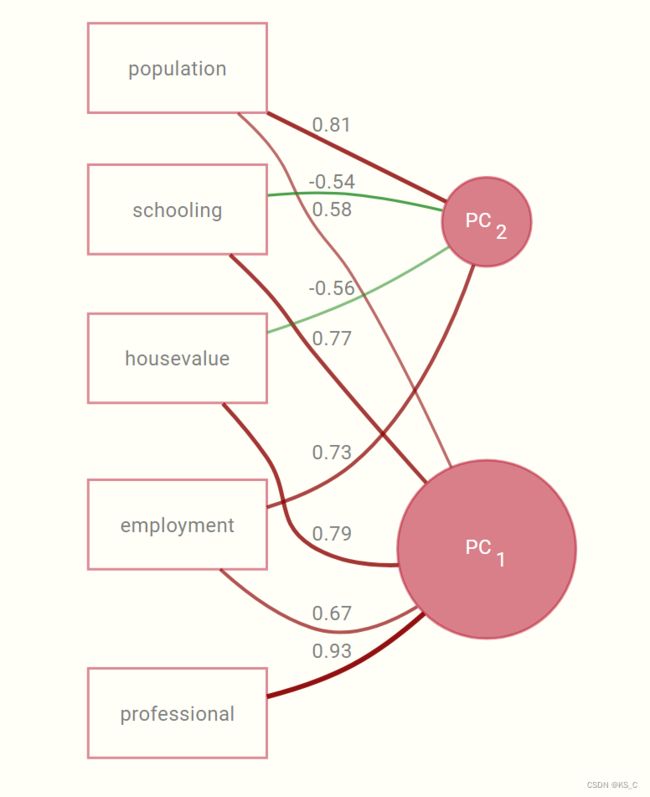
population     0.58  0.81 0.99 0.012  1.8
schooling       0.77 -0.54 0.89 0.115  1.8
employment   0.67  0.73 0.98 0.021  2.0
professional   0.93 -0.10 0.88 0.120  1.0
housevalue     0.79 -0.56 0.94 0.062  1.8

                       PC1  PC2
SS loadings           2.87 1.80
Proportion Var        0.57 0.36
Cumulative Var        0.57 0.93
Proportion Explained  0.62 0.38
Cumulative Proportion 0.62 1.00

Mean item complexity =  1.7
Test of the hypothesis that 2 components are sufficient.

The root mean square of the residuals (RMSR) is  0.03 
 with the empirical chi square  0.29  with prob <  0.59 

Fit based upon off diagonal values = 1

在这个例子中，载荷，也称为模式矩阵（pattern matrix），表示项目与其组件的估计相关性，并提供我们解释因子的关键方式。例如，我们可以通过将观察变量与组件（因子）分数之间的相关联来重现负载，我们稍后会详细讨论。

cor(Harman.5, pc$scores) %>% round(2)

可以看到，源数据中各个变量与两个主成分（pc$scores）之间的相关系数与载荷之间相同。

              PC1   PC2
population   0.58  0.81
schooling    0.77 -0.54
employment   0.67  0.73
professional 0.93 -0.10
housevalue   0.79 -0.56

做相关图：如下，其中红色为负相关，蓝色为正相关，颜色越深则相关性越高。

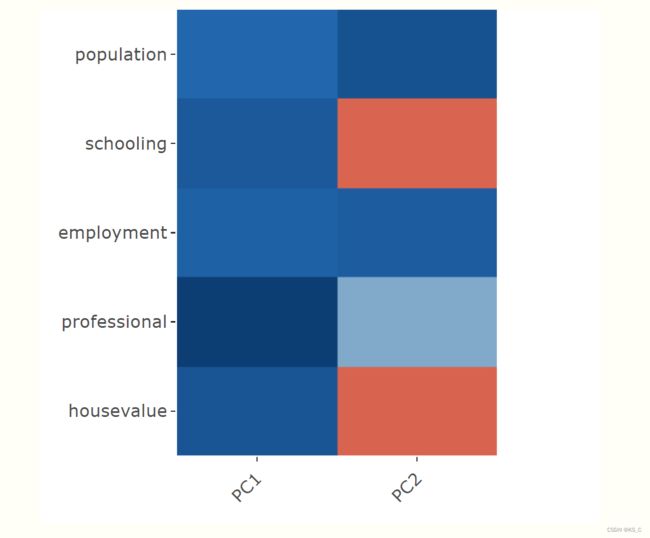
解释是有趣但通常困难的部分。例如，PC1看起来主要是我们的社会经济地位。任何在该组件上得分较高的区域在所有变量上都具有高值。在这一点上值得一提的是命名谬误。仅仅因为我们将一个因素与某个概念联系起来，并不能使它实际上也这样。例如，结果的根本原因可能仅仅是由于人口本身。

该部分其他的几个值：

• h2：保留的几个组件能够解释的项目/变量中的方差的量（一个比值）。它是载荷的平方和，又名共通性（communality）。例如，人口（h2=0.99）几乎完全由这两个个组成部分来解释。
• u2：1 - h2
• com：complexity，衡量复杂程度的标准。如果该变量能够被一个组件完全解释，可以看到值1，否则为零（即完美的简单结构）。例如professional在PC1的载荷为0.93，com=1。

在这种情况下，PCA可能不是最佳选择，也不太可能是最可解释的解决方案。PCA的一个问题是，这种图形模型假设观察到的变量的测量没有误差。此外，默认情况下，主成分彼此不相关，但似乎我们希望允许潜在变量在很多情况下这样做，也许包括这个（不同的旋转会允许这样做）。但是，如果我们的目标仅仅是将 24 个项目减少到几个差异最大的项目，那么这(PCA)将是一种标准技术。

第二部分：

• SS loadings：第一行是载荷的平方和（ sum of the square loadings ）。由于这里是相关矩阵，SS loadings的和为所有变量的个数（在这里是等于5）
• Proportion Var：该成分能够的SS loadings 占总值的多少（比如2.87/5=0.57）
• Cumulative Var：该成分之前的所有成分的累计方差变异

因子分析（Factor Analysis）

现在让我们来看看有时被称为共同因子分析的东西，有时也被称为社会科学中的探索性因素分析（exploratory factor analysis，CFA），甚至是“经典”或“传统”，但通常只是其他地方的因素分析（FA）。虽然我们可以出于类似的原因（降维）同时使用PCA和FA，甚至有类似的解释（考虑载荷），但两者之间有一些潜在的微妙的区别。以一些细节记录这些区别将需要一些矩阵符号，但对于不太热衷于这种呈现的读者，他们可能会注意到图像和结论点。

首先，让我们重新审视PCA，我们可以在概念上将其描述为一种方法，其中我们尝试根据组件的乘积来近似相关矩阵，由我们的载荷矩阵L表示。

R = LL’ 并且 C = XW

C是每个成分的得分，等于每个变量X和权重矩阵W的组合。可以用此成分载荷来估计相关矩阵。

pc_all = principal(Harman.5, nfactors=5,  rotate='none', covar = F)
# loadings（）查看载荷；tcrossprod等同于a和b的转置的内积（结果的第一个数为第一行乘第一列，以此类推）
# tcrossprod（a）为a%*%t（a）
all.equal(tcrossprod(loadings(pc_all)), cor(Harman.5))
#查看

如果我们从以前回到我们的因果思维，因果流起源于观察变量到组件。也许现在我们对载荷的解释变得更清楚了，就像对组分的相关性一样。事实上，我们现在看到，载荷首先被用来创建估计的组件分数。

有了因子分析，事情就不一样了。现在，因果关系是另一个方向，即从潜变量起源。

X = FW（即X约等于因子乘权重）

即使观测到的变量是与之相关的潜变量的一个函数，此外我们也应该考虑独特值$\Psi$，即Factors无法解释的部分，可以看做是误差。

那么现在R = LL’ +KaTeX parse error: Undefined control sequence: \Psy at position 1: \̲P̲s̲y̲

所以在因子分析中我们无法根据载荷矩阵重现相关矩阵。在上述中的pc_all输出结果中，独特值均为0.

fa_all = fa(Harman.5, 
	nfactors=5,  #提取5个因子
	rotate='none', #不旋转
	covar = F,  #输入的是原始数据而非相关矩阵
	fm = 'gls')#因子分解的方法，minres、uls都是最小残差法；wls使用加权最小二乘法；pa主成分分解；gls广义加权最小而成；ml极大似然 等

all.equal(tcrossprod(loadings(fa_all)), cor(Harman.5))          
 # doesn't reproduce cor mat

加上独特值后返回结果为真：

# add uniquenesses
all.equal(tcrossprod(loadings(fa_all)) + diag(fa_all$uniquenesses), cor(Harman.5))

PCA和FA之间的几点差异

• FA关注于相关而PCA关注于方差
• 因子是引起观察变量的原因，变量是结果。
• 因子并不假设变量能够被完美测量

fac = fa(Harman.5, nfactors=2,  rotate='none')
fac

Factor Analysis using method =  minres
Call: fa(r = Harman.5, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
              MR1   MR2   h2     u2 com
population   0.62  0.78 1.00 0.0015 1.9
schooling    0.70 -0.52 0.77 0.2347 1.8
employment   0.70  0.68 0.96 0.0407 2.0
professional 0.88 -0.14 0.80 0.2029 1.1
housevalue   0.78 -0.60 0.97 0.0250 1.9

                       MR1  MR2
SS loadings           2.76 1.74
Proportion Var        0.55 0.35
Cumulative Var        0.55 0.90
Proportion Explained  0.61 0.39
Cumulative Proportion 0.61 1.00

Mean item complexity =  1.7
Test of the hypothesis that 2 factors are sufficient.

The degrees of freedom for the null model are  10  and the objective function was  6.38 with Chi Square of  54.25
The degrees of freedom for the model are 1  and the objective function was  0.35 

The root mean square of the residuals (RMSR) is  0.01 
The df corrected root mean square of the residuals is  0.03 

The harmonic number of observations is  12 with the empirical chi square  0.02  with prob <  0.88 
The total number of observations was  12  with Likelihood Chi Square =  2.5  with prob <  0.11 

Tucker Lewis Index of factoring reliability =  0.582
RMSEA index =  0.507  and the 90 % confidence intervals are  0 0.972
BIC =  0.01
Fit based upon off diagonal values = 1

再说一遍：

• 第一部分（fac$loadings）：因子载荷
  • MR：因子在该变量的载荷
  • h2：共同性，计算方法为载荷的平方和，即这几个因子能够解释的变异的占比（h2是一个比值）
  • u2：特征值（uniqueness，独特值），1-h2,，即因子不能解释的部分
  • com：复杂度complexity，衡量复杂程度的标准，=1时表示完全可以拟合。
  • SS loadings：MR在各个变量上载荷的平方和
  • proportion：该变量SS loading占总SS loading的比
  • cumulative：累计占比
  • proportion explained：loading占所选取的因子loading的比
  • Cumulative Proportion：累计占比
• 其他：后边用到再解释

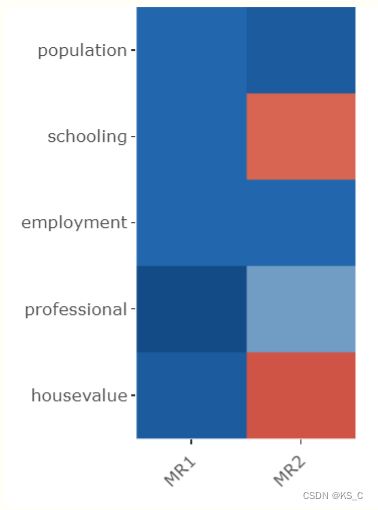
这次的解释有了值得注意的变化，首先，两个因子能够粗略地解释大部分变异（cumulative loadings较高）；其次，没有一个因子能够同时反应所有变量。例如第一个可能能够反应人口普查的健康，第二个反应大小。然而第三个因子较为朦胧，最多能反应教育。所以，由于另外的原因（等下讨论），三个以上的因子有些冗余了。

结构和测量模型

因子分析的其他问题

术语

潜变量的其他用途

• EM算法：一种非常常见的技术，用于估计各种模型情况下的模型参数，它结合了一种潜在变量方法，其中感兴趣的参数被视为潜在变量（例如，属于某个聚类的概率）。
• 项目反应理论：使用潜在变量，特别是在测试情况下（尽管范围更广），来评估物品歧视，学生能力等。请参阅本文档中的相关部分。
• 隐马尔可夫模型：一种通常用于时间序列的潜在变量模型方法。
• 主题模型：在文本分析中，可以根据单词的频率发现潜在的“主题”。请参阅本文档中的相关部分。
• 协同过滤：例如，在电影或音乐的推荐系统中，潜在变量可能表示流派或人口统计子集。
• 高斯过程：全科医生中常见的协方差结构使用因子分析距离。我有斯坦代码演示它。
• 多项式模型：在一些更复杂的多项式回归模型中，因子分析结构用于理解系数的相关性，例如跨类别标签。

总结

潜在变量方法是统计工具箱中必不可少的工具。无论您的目标是压缩数据还是探索潜在的理论动机结构，“因子分析”都将为您服务。

R包

• psych
• lavaan

---

1. 来自洛杉矶大都会标准统计区的数据，包括：Total population（总人口）、Median school years（学校年数中位数）、Total employment（总就业状况）、Miscellaneous professional services（各项混杂的职业服务）、Median house value（房价中位数） ↩︎

2. 由于单位不同，单位更大的变量一般拥有更大的方差，使组件结果偏向于方差较大的variable。因此在进行PCA时要先标准化。 ↩︎

3. covar默认为F，即默认输入数据为标准化后的矩阵（相关系数矩阵）。如果使用原始数据或协方差矩阵则使covar=T ↩︎