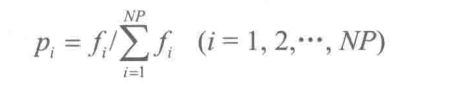万字字符长文带你了解遗传算法(有几个算例源码)
一.遗传算法的基本概念
简单而言,遗传算法使用群体搜索技术,将种群代表一组问题解, 通过对当前种群施加选择、交叉和变异等一系列遗传操作来产生新-一代的种群,并逐步使种群进化到包含近似最优解的状态。由于遗传算法是自然遗传学与计算机科学相互渗透而形成的计算方法,所以遗传算法中经常会使用–些有关自然进化的基础术语,其中的术语对应关系如下所示。
| 遗传学术语 | 遗传算法操作 |
|---|---|
| 群体 | 可行解集 |
| 个体 | 可行解 |
| 染色体 | 可行解的编码 |
| 基因 | 可行解编码的分量 |
| 基因形式 | 遗传编码 |
| 适应度 | 评价函数值 |
| 选择 | 选择操作 |
| 交叉 | 交叉操作 |
| 变异 | 变异操作 |
群体和个体
群体是生物进化过程中的一个集团,表示可行解集。
个体是组成群体的单个生物体,表示可行解。
染色体和基因
染色体是包含生物体所有遗传信息的化合物,表示可行解的编码。基因是控制生物体某种性状(即遗传信息)的基本单位,表示可行解编码的分量。
遗传编码
遗传编码将优化变量转化为基因的组合表示形式,优化变量的编码机制有二进制编码、格雷编码、实数编码、符号编码。
二进制编码
这里介绍- .下二进制编码的原理和实现。例如,求实数区间[0, 4]上函数f(x)的最大值,传统的方法是不断调整自变量x本身的值,直到获得函数最大值;遗传算法则不对参数本身进行调整,而是首先将参数进行编码,形成位串,再对位串进行进化操作。在这里,假设使用二进制编码形式,我们可以由长度为6的位串表示变量x从“00000”到“11111”, 并将中间的取值映射到实数区间[0, 4]内。由于从整数上来看,6位长度的二进制编码位串可以表示0~63,所以对应[0,4]的区间,每个相邻值之间的阶跃值为4/63≈0.0635,这个就是编码精度。一般来说,编码精度越高,所得到的解的质量也越高,意味着解更为优良:但同时,由于遗传操作所需的计算量也更大,因此算法的耗时将更长。因而在解决实际问题时,编码位数需要适当选择。
格雷编码
为改进二进制编码两个整数间海明距离过大的问题,提出了格雷编码。格雷编码是指连续的两个整数所对应的编码之间只有一个码是不同的,其余码位完全相同。二进制编码转格雷编码的公式是:
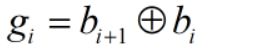
式中:⊕是异或操作,a⊕b表示a和b值不相同则为1,否则为0.
例如,有一个二进制编码为0110,下面演示成对应格雷编码的步骤
- 二进制最右边0和其左边的1做异或,得到1,即得到格雷编码的最右边的数。
- 二进制右边第二位的1和其左边的1异或,得到0,即得到格雷编码右边第二位数。
- 二进制右边第三位数1和其右边的0异或,得到1,即得到格雷编码的右边第三位数。
- 最后最高位保持不变。
最终得到的格雷编码为0101
格雷编码相对于二进制编码的改进,提升了局部瘦身能力。二进制编码由于连续整数之间存在较大的海明距离,不适合进行连续函数的优化问题,且局部搜索能力差。
实数编码
基于二进制编码的个体尽管操作方便,计算简单,但也存在着一些难以克服的困难而无法满足所有问题的要求。例如,对于高维、连续优化问题,由于从一个连续量离散化为一个二进制量本身存在误差,使得算法很难求得精确解。而要提高解的精度又必须加长编码串的长度,造成解空间扩大,算法效率下降。同时,二进制编码也不利于反映所求问题的特定知识,对问题信息和知识利用得不充分也会阻碍算法效率的进一步提高。 为了解决二进制编码产生的问题,人们在解决一些数值优化问题(尤其是高维、连续优化问题)时,经常采用实数编码方式。实数编码的优点是计算精确度高,便于和经典连续优化算法结合,适用于数值优化问题;但其缺点是适用范围有限,只能用于连续变量问题。
符号编码
在使用符号编码时,由于使用符号表示不同的基因,不同的符号不能比较大小,但是符号的顺序不同却可以代表不同的意义。在求解TSP问题时,城市用不同的序号表示,城市之间不能比较大小,但是不同序号的顺序表示经过不同的路径方案。因此在使用符号编码时,交叉编译的结果是对符号顺序的改变,而不是改变符号本身所表达的意义。
符号编码算例见链接:遗传算法求最短路径(旅行商问题)python实现
适应度
适应度即生物群体中个体适应生存环境的能力。在遗传算法中,用来评价个体优劣的数学函数,称为个体的适应度函数。遗传算法在进化搜索中基本上不用外部信息,仅以适应度函数为依据。它的目标函数不受连续可微的约束,且定义域可以为任意集合。对适应度函数的唯一要求是,针对输入可计算出能进行比较的结果。这- -特 点使得遗传算法应用范围很广。在具体应用中,适应度函数的设计要结合求解问题本身的要求而定。适应度函数评估是选择操作的依据,适应度函数设计直接影响到遗传算法的性能。常见的适应度函数构造方法主要有:目标函数映射成适应度函数,基于序的适应度函数等。
遗传操作
遗传操作是优选强势个体的“选择”、个体间交换基因产生新个体的“交叉”、个体基因信息突变而产生新个体的“变异”这三种变换的统称。在生物进化过程中,一个群体中生物特性的保持是通过遗传来继承的。生物的遗传主要是通过选择、交叉、变异三个过程把当前父代群体的遗传信息遗传到下一代(子代)成员。与此对应,遗传算法中最优解的搜索过程也模仿生物的这个进化过程,使用所谓的遗传算子来实现,即选择算子、交叉算子、变异算子。
选择算子
选择操作是指选择种群中适应度较高的个体形成子代种群,常用的选择操作有轮盘赌法 和精英策略。
轮盘赌法
其中,“轮盘赌”选择法是遗传算法中最早提出的一种选择方法,它是一种基于比例的选择,利用各个个体适应度所占比例的大小来决定其子孙保留的可能性。若某个个体i的适应度为fi,种群大小为NP,则它被选取的概率表示为
个体适应度越大,则其被选择的机会也越大;反之亦然。为了选择交叉个体,
需要进行多轮选择。每- -轮产生一个[0,1]内 的均匀随机数,将该随机数作为选择指针来确定被选个体。
原理见代码
#轮盘赌法 选择1个
# -*- coding: utf-8 -*-
import numpy as np
s = [2, 3, 10, 5, 12, 19] # 6个个体的适应度值
s_sum = sum(s) # 所有适应度的和
m = 0
r = np.random.random() # 0-1之间的随机数
c = 0
for i in range(len(s)):
m += s[i] / s_sum
if r <= m:
c = i
break
print(c) # 最后选中个体的序号
#轮盘赌法
import numpy as np
#个体[1,2,3,4,5,6] 抽3个出来, 归一化适应度为p=[0.19,0.22,0.18,0.09,0.13,0.19]
array=np.random.choice([1,2,3,4,5,6],size=3,p=[0.19,0.22,0.18,0.09,0.13,0.19])
print(array)
#输出[2 6 5]
精英策略
精英策略(最优保存策略)是指把适应度最好的个体保留到下一代种群的方法。其基本思路是,当前种群中适应度最高的个体不参与交叉、变异运算,而是用它替换经过交叉、变异等操作后所产生的适应度最低的个体。精英策略可以保证最优个体不会被交叉变异操作所破坏,它是遗传算法收敛性的一个保证,但是另一方面,它也容易使某个局部最优解不易被淘汰而快速扩散,从而使算法的全局搜索能力不强,因此该方法通常与其他方法配合使用。
交叉算子
交叉算子:将群体P(t)中选中的各个个体随机搭配,对每一 对个体,某一概率(交叉概率Pc)交换它们之间的部分染色体。通过交叉,遗传算法的搜索能力得以飞跃提高。
交叉操作一般分为以下几个步骤:首先,从交配池中随机取出要交配的一对个体;然后,根据位串长度L,对要交配的一对个体,随机选取[1,L-1]中的一个或多个整数k作为交叉位置;最后,根据交叉概率P。实施交叉操作,配对个体在交叉位置处,相互交换各自的部分基因,从而形成新的一对个体。
变异算子
变异算子:对群体中的每个个体,以某一概率(变异概率Pm)将某一个或某些基因座上的基因值改变为其他的等位基因值。根据个体编码方式的不同,变异方式有:实值变异、二进制变异。对于二进制的变异,对相应的基因值取反:对于实值的变异,对相应的基因值用取值范围内的其他随机值替代。变异操作的一般步骤为:首先,对种群中所有个体按事先设定的变异概率判断是否进行变异;然后,对进行变异的个体随机选择变异位进行变异。
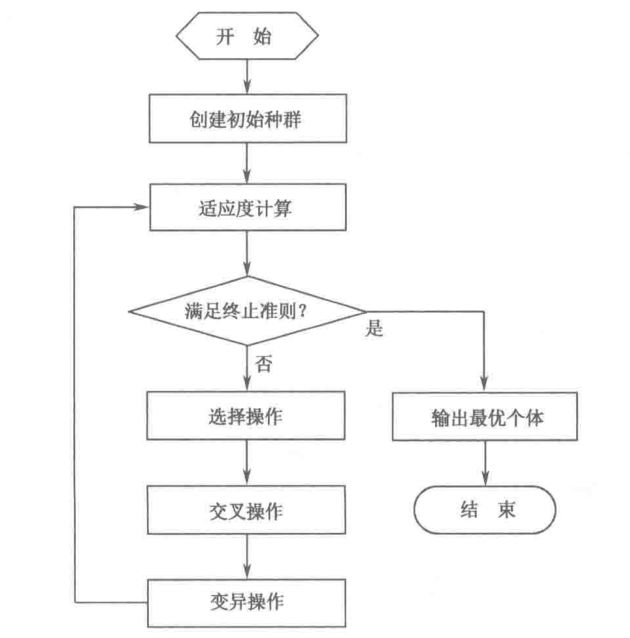
算法流程
算例实现
算例1
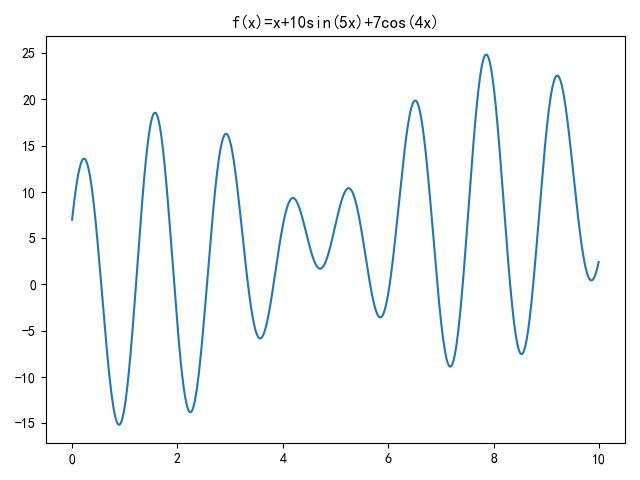
求函数f(x) = x+10sin(5x)+7cos(4x)的最大值,其中x的取值范围为[0,10]。 这是一个有多个局部极值的函数
python版求解
本算例 采取二进制编码 轮盘赌选择算子
函数画图
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
x=np.arange(0,10,0.01)
y=x+10*np.sin(5*x)+7*np.cos(4*x)
plt.plot(x,y)
plt.title('f(x)=x+10sin(5x)+7cos(4x)')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
####################初始化参数#####################
NP=50 #种群数量
L=20 #二进制数串长度
Pc=0.5 #交叉率
Pm=0.1 #变异率
G=100 #最大遗传代数
Xs=10 #上限
Xx=0 #下限
f=np.random.randint(0,2,(NP,L)) #随机获得二进制 初始种群f.shape (50, 20) 数值为0,1 如[[0 1 1 1 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 1]
x=np.zeros((NP,1))#存放种群的实数形式
#nf=f.copy()
nf=np.zeros((NP,L))#下一代种群
Fit=np.zeros((NP,1))#存放适应度值
fitneess_value_list = [] # 每一步迭代的最优解
####################适应度函数#####################
def func1(x):
fit = x + 10 * np.sin(5 * x) + 7 * np.cos(4 * x)
return fit
####################遗传算法循环#####################
for k in range(G):#遍历每一代
### 将二进制解码为定义域范围内十进制 ###
for i in range(NP):#遍历每一个个体
U=f[i,:]#当前个体
m=0
for j in range(L):#L二进制数串长度 # np.power(x1, 3)
m = U[j] * np.power(2,j) + m #np.power(2,j)求2的j次方
x[i] = Xx + m * (Xs - Xx) / (np.power(2,L) - 1) #已经将二进制编码转换到0-10之间的实数啦
Fit[i] = func1(x[i]) #计算当前个体的适应度值
maxFit = np.max(Fit) # 适应度最大值
minFit = np.min(Fit) # 适应度最小值
rr = np.argwhere(Fit == maxFit)[0][0]#查找适应度最大值所对应的个体索引
fBest = f[rr,:] # 历代最优个体 二进制形式
xBest = x[rr] #历代最优个体 实数形式
Fit = (Fit - minFit) / (maxFit - minFit) #归一化适应度值
################# 基于轮盘赌的复制操作 #################
sum_Fit = sum(Fit)
fitvalue = Fit/ sum_Fit #归一化适应度
fitvalue = np.cumsum(fitvalue) #累积求和适应度
ms = np.random.random((NP, 1))
ms = sort([i for i in ms[:, 0]]) #ms为生成NP个 0-1之间的随机数,按从小到大排列
fiti = 0
newi = 0
while newi < NP:#遍历每一个个体
if ms[newi] < fitvalue[fiti]: #
nf[newi,:]=f[fiti,:] #
newi = newi + 1
else:
fiti = fiti + 1
################# 基于概率的交叉操作 #################
#思路 :交换相邻两个个体的部分元素 。如01个体交换 23个体之间交换
for i in range(0,NP,2):
p=np.random.random()#生成一个0-1之间的随机数
if p<Pc:
q=np.random.randint(0,2,(1,L)) #生成一个长度为L的01数组 shape(1,20)
for j in range(L):#遍历个体每一位元素
if q[:,j]==1:
temp=np.int(nf[i+1,j]) #下一个个体(i+1) 的第j个元素
nf[i+1,j]=nf[i,j]
nf[i,j]=temp
################# 基于概率的变异操作 #################
i=0
while i <=np.round(NP*Pm): #np.round(NP*Pm)指定变异个体数
h=np.random.randint(0,NP,1)[0]#随机选择一个(0-NP)之间的整数
for j in range(int(np.round(L*Pm))):#指定变异元素个数
g=np.random.randint(0,L,1)[0] #随机选择一个(0-L)之间的整数
nf[h,g]=np.abs(1- nf[h,g])#将该元素取反
i+=1
f=nf
f[0,:]=fBest#保留最优个体在种群中
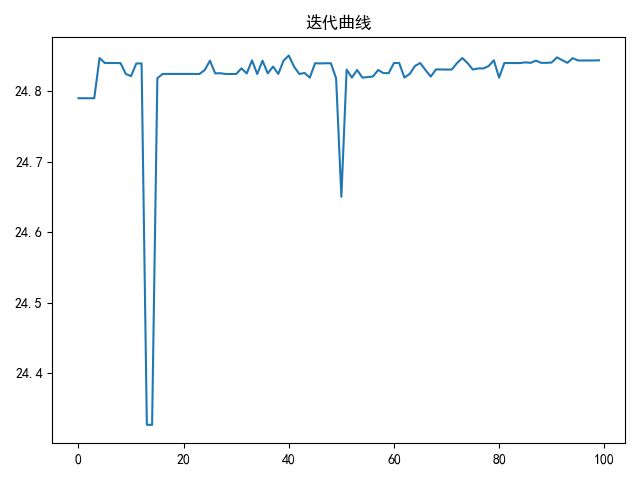
fitneess_value_list.append(maxFit)#存储历代最优适应度
plt.plot(np.array(fitneess_value_list))
plt.title('迭代曲线')
plt.show()
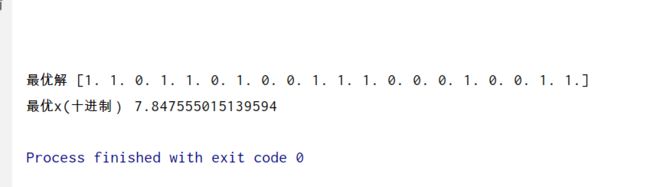
print('最优解',fBest)
m=0
for j in range(L): # L二进制数串长度 # np.power(x1, 3)
m = fBest[j] * np.power(2, j) + m # np.power(2,j)求2的j次方
x = Xx + m * (Xs - Xx) / (np.power(2, L) - 1)
print('最优x(十进制)',x)
从图中看出最优解为24.5左右,参照前面的函数图,发现解正确
精英策略求解代码
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
####################初始化参数#####################
NP=50 #种群数量
L=20 #二进制数串长度
Pc=0.5 #交叉率
Pm=0.1 #变异率
G=100 #最大遗传代数
Xs=10 #上限
Xx=0 #下限
f=np.random.randint(0,2,(NP,L)) #随机获得二进制 初始种群f.shape (50, 20) 数值为0,1 如[[0 1 1 1 0 1 1 1 1 1 0 0 0 1 1 0 1 1 0 1]
x=np.zeros((NP,1))#存放种群的实数形式
nf=np.zeros((NP,L))#下一代种群
k1=4#
Fit=np.zeros((NP,1))#存放适应度值
fitneess_value_list = [] # 每一步迭代的最优解
####################适应度函数#####################
def func1(x):
fit = x + 10 * np.sin(5 * x) + 7 * np.cos(4 * x)
return fit
####################遗传算法循环#####################
for k in range(G):#遍历每一代
### 将二进制解码为定义域范围内十进制 ###
for i in range(NP):#遍历每一个个体
U=f[i,:]#当前个体
m=0
for j in range(L):#L二进制数串长度 # np.power(x1, 3)
m = U[j] * np.power(2,j) + m #np.power(2,j)求2的j次方
x[i] = Xx + m * (Xs - Xx) / (np.power(2,L) - 1) #已经将二进制编码转换到0-10之间的实数啦
Fit[i] = func1(x[i]) #计算当前个体的适应度值
maxFit = np.max(Fit) # 适应度最大值
minFit = np.min(Fit) # 适应度最小值
rr = np.argwhere(Fit == maxFit)[0][0]#查找适应度最大值所对应的个体索引
fBest = f[rr,:] # 历代最优个体 二进制形式
xBest = x[rr] #历代最优个体 实数形式
Fit = (Fit - minFit) / (maxFit - minFit) #归一化适应度值
########精英策略选择个体############
maxkindex=np.argsort(Fit.ravel())[-k1:]#找出适应度值最大的k1个个体索引
nf=f #将当代传到下一代
################# 基于概率的交叉操作 #################
# 思路 :交换相邻两个个体的部分元素 。如01个体交换 23个体之间交换
for i in range(0, NP, 2):
if i not in maxkindex and i+1 not in maxkindex:#如果不是最优那几个个体
p = np.random.random() # 生成一个0-1之间的随机数
if p < Pc:
q = np.random.randint(0, 2, (1, L)) # 生成一个长度为L的01数组 shape(1,20)
for j in range(L): # 遍历个体每一位元素
if q[:, j] == 1:
temp = np.int(nf[i + 1, j]) # 下一个个体(i+1) 的第j个元素
nf[i + 1, j] = nf[i, j]
nf[i, j] = temp
################# 基于概率的变异操作 #################
i=0
while i <=np.round(NP*Pm): #np.round(NP*Pm)指定变异个体数
h=np.random.randint(0,NP,1)[0]#随机选择一个(0-NP)之间的整数
if h not in maxkindex:#如果选中的不是最优那几个个体
for j in range(int(np.round(L*Pm))):#指定变异元素个数
g=np.random.randint(0,L,1)[0] #随机选择一个(0-L)之间的整数
nf[h,g]=np.abs(1- nf[h,g])#将该元素取反
i+=1
f = nf
f[0, :] = fBest # 保留最优个体在种群中
fitneess_value_list.append(maxFit) # 存储历代最优适应度
plt.plot(np.array(fitneess_value_list))
plt.title('迭代曲线')
plt.show()
print('最优解',fBest)
m=0
for j in range(L): # L二进制数串长度 # np.power(x1, 3)
m = fBest[j] * np.power(2, j) + m # np.power(2,j)求2的j次方
x = Xx + m * (Xs - Xx) / (np.power(2, L) - 1)
print('最优x(十进制)',x)
算例2
求解Z=2a+xx-acos2πx+yy-acos2πy的极小值
import numpy as np
import matplotlib.pyplot as plt
def fitness_func(X):
# 目标函数,即适应度值,X是种群的表现型
a = 10
pi = np.pi
x = X[:, 0]
y = X[:, 1]
return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)
def decode(x, a, b):
"""解码,即基因型到表现型"""
xt = 0
for i in range(len(x)):
xt = xt + x[i] * np.power(2, i)
return a + xt * (b - a) / (np.power(2, len(x)) - 1)
def decode_X(X: np.array):
"""对整个种群的基因解码,上面的decode是对某个染色体的某个变量进行解码"""
X2 = np.zeros((X.shape[0], 2))
for i in range(X.shape[0]):
xi = decode(X[i, :20], -5, 5)
yi = decode(X[i, 20:], -5, 5)
X2[i, :] = np.array([xi, yi])
return X2
def select(X, fitness):
"""根据轮盘赌法选择优秀个体"""
fitness = 1 / fitness # fitness越小表示越优秀,被选中的概率越大,做 1/fitness 处理
fitness = fitness / fitness.sum() # 归一化
idx = np.array(list(range(X.shape[0])))
X2_idx = np.random.choice(idx, size=X.shape[0], p=fitness) # 根据概率选择
X2 = X[X2_idx, :]
return X2
def crossover(X, c):
"""按顺序选择2个个体以概率c进行交叉操作"""
for i in range(0, X.shape[0], 2):
xa = X[i, :]
xb = X[i + 1, :]
for j in range(X.shape[1]):
# 产生0-1区间的均匀分布随机数,判断是否需要进行交叉替换
if np.random.rand() <= c:
xa[j], xb[j] = xb[j], xa[j]
X[i, :] = xa
X[i + 1, :] = xb
return X
def mutation(X, m):
"""变异操作"""
for i in range(X.shape[0]):
for j in range(X.shape[1]):
if np.random.rand() <= m:
X[i, j] = (X[i, j] + 1) % 2
return X
def ga():
"""遗传算法主函数"""
c = 0.3 # 交叉概率
m = 0.05 # 变异概率
best_fitness = [] # 记录每次迭代的效果
best_xy = []
iter_num = 100 # 最大迭代次数
X0 = np.random.randint(0, 2, (50, 40)) # 随机初始化种群,为50*40的0-1矩阵
for i in range(iter_num):
X1 = decode_X(X0) # 染色体解码
fitness = fitness_func(X1) # 计算个体适应度
X2 = select(X0, fitness) # 选择操作
X3 = crossover(X2, c) # 交叉操作
X4 = mutation(X3, m) # 变异操作
# 计算一轮迭代的效果
X5 = decode_X(X4)
fitness = fitness_func(X5)
best_fitness.append(fitness.min())
x, y = X5[fitness.argmin()]
best_xy.append((x, y))
X0 = X4
# 多次迭代后的最终效果
print("最优值是:%.5f" % best_fitness[-1])
print("最优解是:x=%.5f, y=%.5f" % best_xy[-1])
# 最优值是:0.00000
# 最优解是:x=0.00000, y=-0.00000
# 打印效果
plt.plot(best_fitness, color='r')
plt.show()
ga()


算例3
前面都是讲解的二进制编码,下面讲解下实数编码
例子见链接:
https://blog.csdn.net/kobeyu652453/article/details/109527260
本文通过源代码 和算例介绍了遗传算法基本流程、以及二进制编码、实数编码、轮盘赌和精英策略选择算子、基于概率的交叉和变异算子。下篇博客通过源码介绍遗传算法如何求解带约束问题
遗传算法求解带约束优化问题(源码实现)
![]()
作者:电气 余登武