逆概率加权&Doubly Robust Methods
1. 逆概率加权
1.1 为什么要用逆概率加权
逆概率加权是一种debiasing方法,可以用于纠正样本分布不均衡导致的辛普森悖论等问题。
1.2 逆概率加权推导
逆概率加权是后门调整的进一步推广,利用贝叶斯公式对后门调整公式变换了一下形式。
P ( y ∣ d o ( t ) ) = ∑ x P ( y ∣ t , x ) ∗ P ( x ) ‾ = ∑ x P ( y ∣ t , x ) ∗ P ( x ) ∗ P ( t ∣ x ) P ( t ∣ x ) = ∑ x P ( y , t , x ) P ( t ∣ x ) \begin{aligned} P(y|do(t)) &= \sum_x P(y|t,x)*\underline {P(x)} \\ &= \sum_x \frac {P(y|t,x)*P(x)*P(t|x)}{P(t|x)} \\ &= \sum_x \frac {P(y,t,x)}{P(t|x)} \\ \end{aligned} P(y∣do(t))=x∑P(y∣t,x)∗P(x)=x∑P(t∣x)P(y∣t,x)∗P(x)∗P(t∣x)=x∑P(t∣x)P(y,t,x)
另一种证明方式:
P ( y ∣ d o ( t ) ) = ∑ x P ( y ∣ t , x ) ∗ P ( x ) ‾ P ( y ∣ t ) = ∑ x P ( y ∣ t , x ) ∗ P ( t ∣ x ) ‾ = ∑ x P ( y , x ∣ t ) \begin{aligned} P(y|do(t)) &= \sum_x P(y|t,x)*\underline {P(x)} \\ P(y|t) &= \sum_x P(y|t,x)* \underline {P(t|x)} = \sum_x P(y,x|t) \\ \end{aligned} P(y∣do(t))P(y∣t)=x∑P(y∣t,x)∗P(x)=x∑P(y∣t,x)∗P(t∣x)=x∑P(y,x∣t)
如果reweight population 使得 P ( t ∣ x ) P(t|x) P(t∣x)= P ( t ) P(t) P(t),那么 P ( y ∣ d o ( t ) ) P(y|do(t)) P(y∣do(t))和 P ( y ∣ t ) P(y|t) P(y∣t)相等,从图的角度,即为切断了 X → T X \rightarrow T X→T的后门路径,得到的是causal association
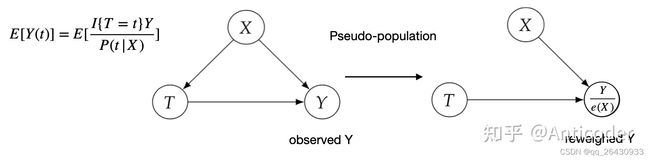
具体ATE计算方法:
- Idetification: τ = E [ Y ( 1 ) − Y ( 0 ) ) ] = E [ I { T = 1 } Y P ( T ∣ X ) ] − E [ I { T = 0 } Y P ( T ∣ X ) ] \tau = E[Y(1)-Y(0))]= E[\frac {I \{T=1\} Y}{P(T|X)}] - E[\frac {I \{T=0\} Y}{P(T|X)}] τ=E[Y(1)−Y(0))]=E[P(T∣X)I{T=1}Y]−E[P(T∣X)I{T=0}Y]
- Estimation: τ ^ = 1 N ∑ i = 1 N T i Y i e ^ ( X i ) − 1 N ∑ i = 1 N ( 1 − T i ) Y i 1 − e ^ ( X i ) \hat \tau = \frac{1}{N} \sum_{i=1}^N \frac{T_i Y_i}{\hat e(X_i)}-\frac{1}{N} \sum_{i=1}^N \frac{(1-T_i) Y_i}{1-\hat e(X_i)} τ^=N1∑i=1Ne^(Xi)TiYi−N1∑i=1N1−e^(Xi)(1−Ti)Yi
1.3 逆概率加权举例说明
原始样本分布
| 类别 | T =1 | T=0 | P ( T = 1 | X = 1 ) P(T=1|X=1) P(T=1|X=1) |
|---|---|---|---|
| X=1 | 8 | 2 | 8 10 = 0.8 \frac {8}{10}=0.8 108=0.8 |
| X=0 | 10 | 6 | 10 16 = 0.625 \frac {10}{16}=0.625 1610=0.625 |
reweighted
| 类别 | T =1 | T=0 | P ( T = 1 | X = 1 ) P(T=1|X=1) P(T=1|X=1) |
|---|---|---|---|
| X=1 | 8 0.8 = 10 \frac {8}{0.8}=10 0.88=10 | 8 1 − 0.8 = 10 \frac {8}{1-0.8}=10 1−0.88=10 | 10 10 + 10 = 0.5 \frac {10}{10+10}=0.5 10+1010=0.5 |
| X=0 | 10 0.625 = 16 \frac {10}{0.625}=16 0.62510=16 | 6 1 − 0.625 = 16 \frac {6}{1-0.625}=16 1−0.6256=16 | 16 16 + 16 = 0.5 \frac {16}{16+16}=0.5 16+1616=0.5 |
原始样本分布 VS reweighted
| 类别 | P ( T = 1 | X = 1 ) P(T=1|X=1) P(T=1|X=1) | P ( T = 1 | X = 0 ) P(T=1|X=0) P(T=1|X=0) | P ( T = 1 ) P(T=1) P(T=1) |
|---|---|---|---|
| original | 0.8 | 0.625 | 8 + 10 10 + 16 = 0.69 \frac {8+10}{10+16}=0.69 10+168+10=0.69 |
| reweighted | 0.5 | 0.5 | 0.5 |
reweighted之后 P ( t ∣ x ) = P ( t ) = 0.5 P(t|x) = P(t)=0.5 P(t∣x)=P(t)=0.5
1.4 逆概率加权缺点
0.2.4 Covariate balancing propensity score (CBPS)
因果推断综述解析|A Survey on Causal Inference(3)
倾向得分方法的双重稳健且有效的改进
IPW方法的倾向得分其实是策略的倾向选择概率,但是选择性偏差带来的是样本之间其他相关变量分布的不平衡。所以使用逆倾向得分属于只考虑了策略的倾向选择概率,却用来平衡样本之间其他相关变量的分布。Covariate balancing propensity score (CBPS),协变量平衡倾向得分方法被设计出来来同时衡量这两方面,来使倾向得分更准确。CBPS得到倾向得分的方式是求解下面的方程:
2. Doubly Robust Methods
2.1 为什么要用Doubly Robust
逆概率加权方法虽然简单易行,但是对于倾向得分的设定非常敏感。该方法有两个弱点:
- 需要对倾向指数的估计足够精确
- 如果倾向指数过于趋近0或1,就会导致某些权重的值过高,使估计出的平均因果效应的方差过大
Doubly Robust 公式
A ^ T E = 1 N ∑ i = 1 N ( T i ( Y i − μ ^ 1 ( X i ) ) e ^ ( X i ) + μ ^ 1 ( X i ) ) − 1 N ∑ i = 1 N ( ( 1 − T i ) ( Y i − μ ^ 0 ( X i ) ) e ^ ( X i ) + μ ^ 0 ( X i ) ) \hat ATE = \frac{1}{N} \sum_{i=1}^N \left( \frac{T_i (Y_i-\hat \mu_1(X_i))}{\hat e(X_i) }+\hat \mu_1(X_i) \right) -\frac{1}{N} \sum_{i=1}^N \left( \frac{(1-T_i) (Y_i-\hat \mu_0(X_i))}{\hat e(X_i) }+\hat \mu_0(X_i) \right) A^TE=N1i=1∑N(e^(Xi)Ti(Yi−μ^1(Xi))+μ^1(Xi))−N1i=1∑N(e^(Xi)(1−Ti)(Yi−μ^0(Xi))+μ^0(Xi))
μ ^ 1 ( X i ) : e s t i m a t i o n o f E [ Y ∣ X , T = 1 ] \hat \mu_1(X_i):estimation \ of E[Y|X,T=1] μ^1(Xi):estimation ofE[Y∣X,T=1]
μ ^ 1 ( X 0 ) : e s t i m a t i o n o f E [ Y ∣ X , T = 0 ] \hat \mu_1(X_0):estimation\ of E[Y|X,T=0] μ^1(X0):estimation ofE[Y∣X,T=0]
e ^ ( X i ) : e s t i m a t i o n o f E [ T = 1 ∣ X ] \hat e(X_i) :estimation \ of E[T=1|X] e^(Xi):estimation ofE[T=1∣X]
2.2 Doubly Robust推导
需证明: A ^ T E = E ( Y 1 ) − E ( Y 0 ) \hat ATE =E(Y_1) - E(Y_0) A^TE=E(Y1)−E(Y0)
首先证明: E ^ ( Y 1 ) = 1 N ∑ i = 1 N ( T i ( Y i − μ ^ 1 ( X i ) ) e ^ ( X i ) + μ ^ 1 ( X i ) ) \hat E(Y_1) = \frac{1}{N} \sum_{i=1}^N \left( \frac{T_i (Y_i-\hat \mu_1(X_i))}{\hat e(X_i) }+\hat \mu_1(X_i) \right) E^(Y1)=N1∑i=1N(e^(Xi)Ti(Yi−μ^1(Xi))+μ^1(Xi))
- 假设 μ ^ 1 ( X ) \hat \mu_1(X) μ^1(X)正确,则 E [ T i ( Y i − μ ^ 1 ( X i ) ] = 0 E[T_i (Y_i-\hat \mu_1(X_i)]=0 E[Ti(Yi−μ^1(Xi)]=0,因为乘以 T i T_i Ti只选择了观测值为 T = 1 T=1 T=1的样本,这些样本由 μ ^ 1 \hat \mu_1 μ^1估计的残差的期望是0(根据定义),同样根据定义, E ^ ( Y 1 ) = E ( μ ^ 1 ( X i ) ) \hat E(Y_1) =E(\hat \mu_1(X_i)) E^(Y1)=E(μ^1(Xi))
- 假设 e ^ ( X ) \hat e(X) e^(X)正确,则 E [ T i − e ^ ( X i ) ] = 0 E[T_i- \hat e(X_i)]=0 E[Ti−e^(Xi)]=0,且根据逆概率加权, E ^ ( Y 1 ) = 1 N ∑ i = 1 N T i Y i e ^ ( X i ) \hat E(Y_1) =\frac{1}{N} \sum_{i=1}^N \frac{T_i Y_i}{\hat e(X_i) } E^(Y1)=N1∑i=1Ne^(Xi)TiYi
E ^ ( Y 1 ) = 1 N ∑ i = 1 N ( T i ( Y i − μ ^ 1 ( X i ) ) e ^ ( X i ) + μ ^ 1 ( X i ) ) = 1 N ∑ i = 1 N ( T i Y i e ^ ( X i ) − T i μ ^ 1 ( X i ) e ^ ( X i ) + μ ^ 1 ( X i ) ) = 1 N ∑ i = 1 N [ T i Y i e ^ ( X i ) − ( T i − e ^ ( X i ) e ^ ( X i ) ) μ ^ 1 ( X i ) ] \begin{aligned} \hat E(Y_1) &= \frac{1}{N} \sum_{i=1}^N \left( \frac{T_i (Y_i-\hat \mu_1(X_i))}{\hat e(X_i) }+\hat \mu_1(X_i) \right) \\ &= \frac{1}{N} \sum_{i=1}^N \left( \frac{T_i Y_i}{\hat e(X_i) } - \frac{T_i \hat \mu_1(X_i)}{\hat e(X_i) }+\hat \mu_1(X_i) \right) \\ &= \frac{1}{N} \sum_{i=1}^N \left[ \frac{T_i Y_i}{\hat e(X_i) } - \left( \frac{T_i - \hat e(X_i)}{\hat e(X_i) } \right) \hat \mu_1(X_i)\right] \\ \end{aligned} E^(Y1)=N1i=1∑N(e^(Xi)Ti(Yi−μ^1(Xi))+μ^1(Xi))=N1i=1∑N(e^(Xi)TiYi−e^(Xi)Tiμ^1(Xi)+μ^1(Xi))=N1i=1∑N[e^(Xi)TiYi−(e^(Xi)Ti−e^(Xi))μ^1(Xi)]
2.3 Doubly Robust例子
数据预处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
#读取数据
data = pd.read_csv('/Users/wujunhan/Downloads/causal inference learning/learning_mindset.csv')
print (data.columns)
#get_dummy
categ = ["ethnicity", "gender", "school_urbanicity"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]
data_with_categ = pd.concat([
data.drop(columns=categ), # dataset without the categorical features
pd.get_dummies(data[categ], columns=categ, drop_first=False) # categorical features converted to dummies
], axis=1)
print(data_with_categ.shape)
三种模型计算ATE
T = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])
#doubly_robust
from sklearn.linear_model import LogisticRegression, LinearRegression
def doubly_robust(df, X, T, Y):
ps = LogisticRegression(C=1e6).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
mu0 = LinearRegression().fit(df.query(f"{T}==0")[X], df.query(f"{T}==0")[Y]).predict(df[X])
mu1 = LinearRegression().fit(df.query(f"{T}==1")[X], df.query(f"{T}==1")[Y]).predict(df[X])
ATE = np.mean(df[T]*(df[Y] - mu1)/ps + mu1) - \
np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
return (round(ATE,3))
doubly_robust(data_with_categ, X, T, Y)
#wrong_ps
def doubly_robust_wrong_ps(df, X, T, Y):
# wrong PS model
np.random.seed(654)
ps = np.random.uniform(0.1, 0.9, df.shape[0])
mu0 = LinearRegression().fit(df.query(f"{T}==0")[X], df.query(f"{T}==0")[Y]).predict(df[X])
mu1 = LinearRegression().fit(df.query(f"{T}==1")[X], df.query(f"{T}==1")[Y]).predict(df[X])
ATE = np.mean(df[T]*(df[Y] - mu1)/ps + mu1) - \
np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
return (round(ATE,3))
doubly_robust_wrong_ps(data_with_categ, X, T, Y)
#wrong mux model
def doubly_robust_wrong_model(df, X, T, Y):
np.random.seed(654)
ps = LogisticRegression(C=1e6).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
# wrong mu(x) model
mu0 = np.random.normal(0, 1, df.shape[0])
mu1 = np.random.normal(0, 1, df.shape[0])
ATE = np.mean(df[T]*(df[Y] - mu1)/ps + mu1) - \
np.mean((1-df[T])*(df[Y] - mu0)/(1-ps) + mu0)
return (round(ATE,3))
doubly_robust_wrong_model(data_with_categ, X, T, Y)
boostrap算ATE置信区间
from joblib import Parallel, delayed # for parallel processing
np.random.seed(88)
# run 1000 bootstrap samples
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(doubly_robust)(data_with_categ.sample(frac=1, replace=True), X, T, Y)
for _ in range(bootstrap_sample))
ates = np.array(ates)
print(f"true model,ATE 95% CI:", (round(np.percentile(ates, 2.5),3), round(np.percentile(ates, 97.5),3)))
np.random.seed(88)
parallel_fn = delayed(doubly_robust_wrong_ps)
wrong_ps = Parallel(n_jobs=4)(parallel_fn(data_with_categ.sample(frac=1, replace=True), X, T, Y)
for _ in range(bootstrap_sample))
wrong_ps = np.array(wrong_ps)
print(f"wrong ps model,ATE 95% CI:", (round(np.percentile(wrong_ps, 2.5),3), round(np.percentile(wrong_ps, 97.5),3)))
np.random.seed(88)
parallel_fn = delayed(doubly_robust_wrong_model)
wrong_mux = Parallel(n_jobs=4)(parallel_fn(data_with_categ.sample(frac=1, replace=True), X, T, Y)
for _ in range(bootstrap_sample))
wrong_mux = np.array(wrong_mux)
print(f"wrong mux model ATE 95% CI:", (round(np.percentile(wrong_mux, 2.5),3), round(np.percentile(wrong_mux, 97.5),3)))
一些记录
作者在例子中get_dummies的drop_first 设置为False,和设置为True结果是一致的,因为共线性不影响线性模型的预测结果y,但是不剔除第一列,会引起共线性,导致线性模型的系数估计不准确
data_with_categ['gender_2'].corr(data_with_categ['gender_1'])
相关系数为-0.99999
3.参考资料
因果推断总结
IPW例子
Doubly Robust通俗讲解
Doubly Robust严格推导
Doubly Robust参考