基于R语言的回归分析实现
目录
1.一元线性模型
1.1绘制散点图
1.2回归参数的估计
1.3回归方程的显著性检验
1.4线性模型常用函数
2.软件实现
2.1绘制散点图
2.2计算回归
2.3做预测
2.4残差分析
2.5回归诊断分析
3.多元线性模型
3.1模型建立
3.2代码实现
3.3做预测
3.4残差分析
3.5回归诊断分析
1.一元线性模型
一元线性模型一般用于描述因变量随自变量之间的线性模型一般为：
其中，
表示Y随X的变化而线性变化的部分;
是随机误差。
1.1绘制散点图
一般情况下可以对数据绘制一个散点图，散点图可以直观的观察出X，Y之间的关系。
1.2回归参数的估计
求出位置参数
，
的估计值，要使得散点图尽可能分布在直线的两侧且越接近效果越好。
1.3回归方程的显著性检验
从回归参数的估计公式可知，在计算过程中并不一定要知道Y与X是否有线性相关的关系，但如果不存在这种关系，那么求得的回妇方程毫无意义。因此，需要对回归方程进行检验.从统计上讲，是E(Y)随X线性变化的变化率，若β1=0,则E(Y)实际上并不随X作线性变化，仅当β1≠0时，E(Y)才随X作线性变化,也仅在这时一元线性回归方程才有意义.因此假设检验为:
. 
一般有三种检验方法；
1）T检验法
2）F检验法
3）相关系数检验法
当拒绝H0时，我们二五年为回归方程是显著的。
1.4线性模型常用函数
1）lm()函数
2）summary()函数
3）predict()函数
2.软件实现
合金强度与碳含量之间的关系数据：
| 碳含量X | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.20 | 0.21 | 0.23 |
| 强度Y | 42.0 | 43.5 | 45.0 | 45.5 | 45.0 | 47.5 | 49.0 | 53.0 | 50.0 | 55.0 |
55.0 | 60 |
2.1绘制散点图
data<-read.table("D:/桌面文件/数据.txt")
x<-data[[1]]
y<-data[[2]]
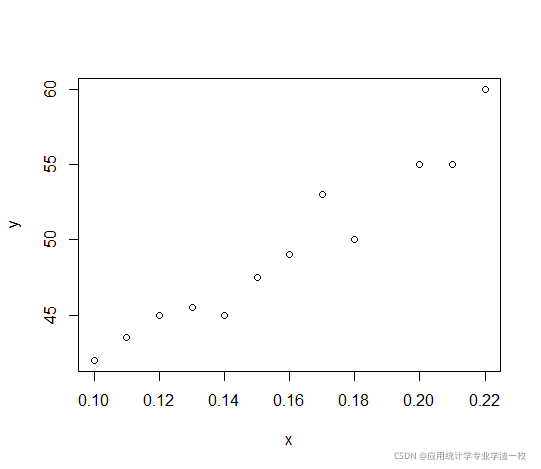
plot(x,y)
从图可知，散点图的分布接近于一条直线，因此我们可以试着用一元线性模型来拟合。
2.2计算回归
data<-read.table("D:/桌面文件/数据.txt")
x<-data[[1]]
y<-data[[2]]
#建立一元回归方程
lm.sol<-lm(y~1+x)
#模型汇总
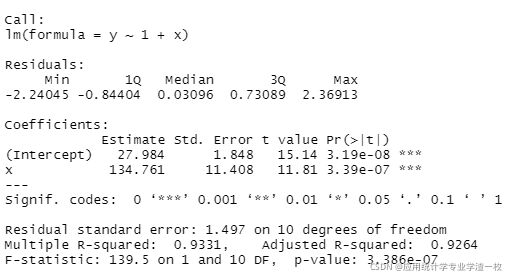
summary(lm.sol)运行结果：
其中：
Residuals：残差的最小值，分位数，最大值；
Coefficients：Estimate为回归参数的估计，std.error为回归参数的标准差，t_value为P值；
其中***说明极为显著，**说明高度显著，*说明显著，·说明不太显著，没有记号为不显著。
F-statistic：为F统计量。
那么我们可以得到回归方程为：
Y=27.984X+134.761
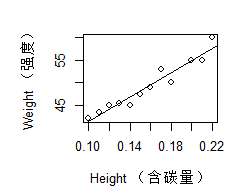
拟合图：
plot(x,y,
xlab = "Height （含碳量）",
ylab = "Weight （强度）")
abline(lm.sol)
2.3做预测
给出x的值
preds<-data.frame(x=0.24)
#做区间预测，精度为95%
predict(lm.sol,newdata = preds,interval = "prediction",level = 0.95)运行结果：
从图中可以看出，预测值为60.32608，置信区间为[56.26977，64.38238]。
2.4残差分析
#一切子集逐步回归
lm.step<-step(lm.sol,direction = "both")
#计算标准残差
y.rst<-rstandard(lm.step)
#计算模型的预测值
y.fit<-predict(lm.step)
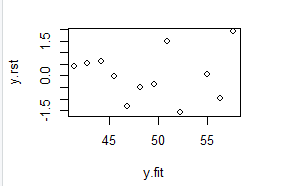
#绘制残差散点图
plot(y.rst~y.fit)
从图中来看，没有异常值点。因此不需要剔除数据。
2.5回归诊断分析
#创建图窗
par(mfrow=c(2,2))
#绘制模型诊断图
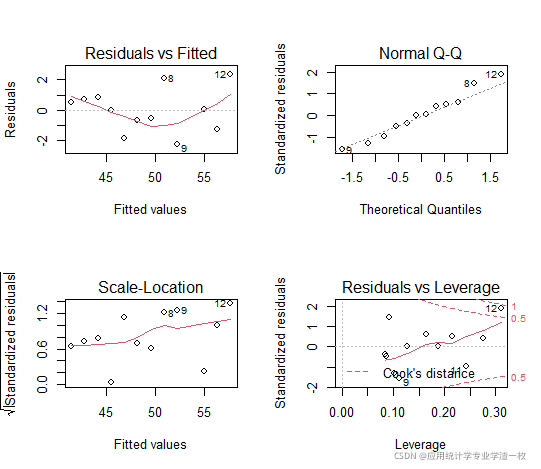
plot(lm.step)运行结果：
第一个图为残差-拟合图，在图中的点基本上呈随机分布；第二个为正态Q-Q图，图中的点基本落在一条直线上，认为残差服从正态分布；第三个为大小-位置图，第四个为残差杠杆图，以小组形式存在，分布在中心的周围。
3.多元线性模型
3.1模型建立
Y=B0+B1X1+B2X2
根据经验，在人的身高相等的情况下，血压的收缩压￥与体重X(千克),年龄X(岁数）有关．现收集了13个男子的数据，试建立Y关于X1，X2,的线性回归方程.
3.2代码实现
data<-read_xlsx("D:/桌面文件/11.xlsx")
#建立回归模型
lm.sol<-lm(Y~X1+X2,data = data)
#模型汇总
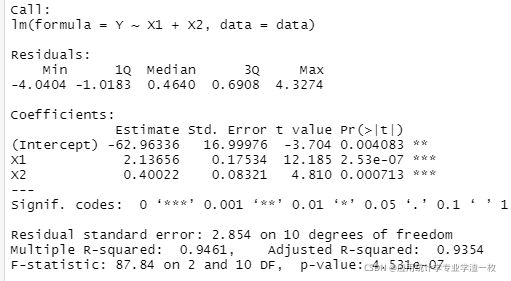
summary(lm.sol)运行结果：
从图中可知，我们可以知道，回归系数与回归方程的检验都是显著性的，都符合要求，因此我们可以得到回归方程：
Y=2.13656X1+0.40022X2-62.96336
3.3做预测
#给出x1，x2
preds<-data.frame(X1=95,X2=50)
#做区间预测，精度为95%
predict(lm.sol,newdata = preds,interval = "prediction",level = 0.95)运行结果：
从图中来看，预测值为160.0205，置信区间为：[150.8997,169.1412]。
3.4残差分析
#一切子集逐步回归
lm.step<-step(lm.sol,direction = "both")
#计算标准残差
y.rst<-rstandard(lm.step)
#计算模型的预测值
y.fit<-predict(lm.step)
#绘制残差散点图
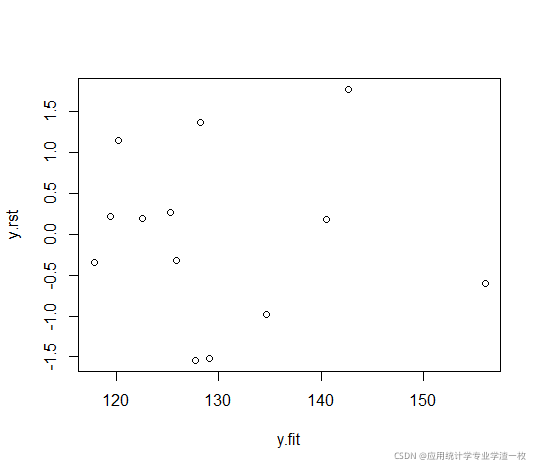
plot(y.rst~y.fit)运行结果：
从图中来看，几乎没有异常值点，因此不需要剔除数据。
3.5回归诊断分析
#创建图窗
par(mfrow=c(2,2))
#绘制模型诊断图
plot(lm.step)
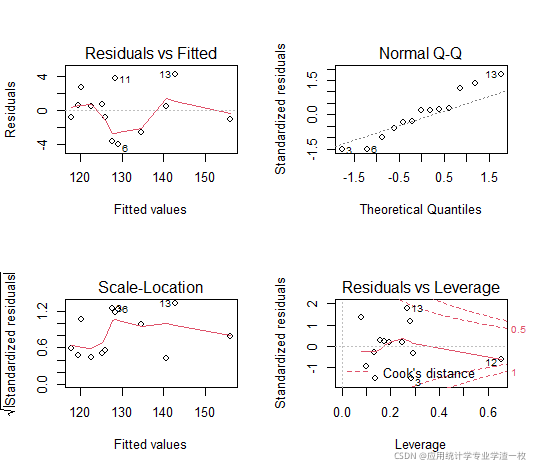
运行结果：
第一个图为残差-拟合图，在图中的点基本上呈随机分布；第二个为正态Q-Q图，图中的点基本落在一条直线上，认为残差服从正态分布；第三个为大小-位置图，第四个为残差杠杆图，以小组形式存在，分布在中心的周围。