使用R语言进行一元回归
使用R语言进行一元回归
我们通过一个例子来介绍通过R语言进行一元回归的方法
例子: 为研究某实验过程中,温度x(℃)对产品得率(%)的影响,测得数据如下:
| 温度x(℃) | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
|---|---|---|---|---|---|---|---|---|---|---|
| 得率Y(%) | 45 | 51 | 54 | 61 | 66 | 70 | 74 | 78 | 85 | 89 |
说明:该例子来自盛骤等老师编写的第四版概率论与数理统计书籍
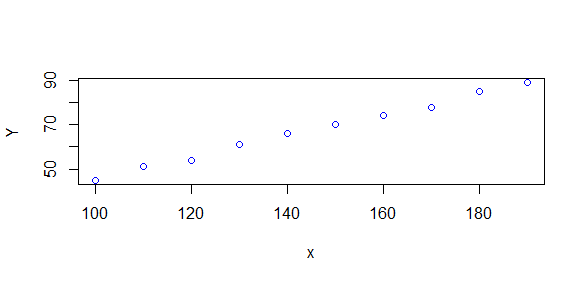
首先,我们把x,Y数值之间的联系先用散点图描绘出来:
p = c(100,110,120,130,140,150,160,170,180,190)
q = c(45,51,54,61,66,70,74,78,85,89)
plot(p,q,type="p",col="blue",xlab="x",ylab="Y")
从上面散点图我们可以看出,x与Y之间的相关性很强,近似一种线性关系。一元回归的目的就是拟合出一条回归直线,使得散点图上的每一点与这条直线的纵向距离最短。通过拟合出的回归直线,可以用于预测。
设: Y = a + b x + ε , ε N ( 0 , σ 2 ) Y=a+bx+ε,ε~N(0,σ^2) Y=a+bx+ε,ε N(0,σ2)
对参数a,b进行估计:
其中:
b ^ = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 \hat{b}=\dfrac{\sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2} b^=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
a ^ = y ˉ − b ^ x ˉ \hat{a}=\bar{y}-\hat{b} \bar{x} a^=yˉ−b^xˉ
y = a ^ + b ^ x ˉ y=\hat{a}+ \hat{b} \bar{x} y=a^+b^xˉ即为Y关于x的回归方程。
现在,我们使用R语言来求参数a和b
方法一:
p = c(100,110,120,130,140,150,160,170,180,190)
q = c(45,51,54,61,66,70,74,78,85,89)
plot(p,q,type="p",col="blue",xlab="x",ylab="Y")
lxy<-function(x,y){n=length(x);sum(x*y)-sum(x)*sum(y)/n} #自定义函数
b = lxy(p,q)/lxy(p,p)
a = mean(q)-b*mean(p)
print(b)
print(a)
lines(p,a+b*p)
运行结果:
[1] 0.4830303
[1] -2.739394
函数图像:
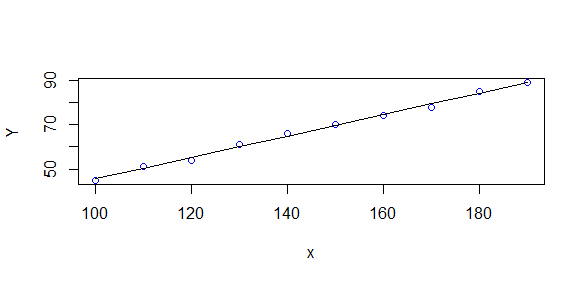
即:回归方程为 Y = − 2.739394 + 0.4830303 ∗ x Y=-2.739394+0.4830303*x Y=−2.739394+0.4830303∗x
方法二:(简单,推荐)
p = c(100,110,120,130,140,150,160,170,180,190)
q = c(45,51,54,61,66,70,74,78,85,89)
r=lm(q~1+p)
print(summary(r))
运行结果:
Call:
lm(formula = q ~ 1 + p)
Residuals:
Min 1Q Median 3Q Max
-1.3758 -0.5591 0.1242 0.7470 1.1152
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.73939 1.54650 -1.771 0.114
p 0.48303 0.01046 46.169 5.35e-11 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9503 on 8 degrees of freedom
Multiple R-squared: 0.9963, Adjusted R-squared: 0.9958
F-statistic: 2132 on 1 and 8 DF, p-value: 5.353e-11
R中提供了lm( )函数来进行回归分析,使用summary( )可以得到回归结果的所有参数。其中,p后面的三个星号***表示参数的估计是很显著的。