R语言进行COX时变系数模型(含时间依存协变量的Cox回归模型)
我们在临床研究中,经常要研究疾病与生存率的关系,cox回归是用得比较常见的模型之一。Cox 比例风险模型依赖于风险随时间变化的假设(PH假设),意思是协变量对结局的影响随着时间变化是固定的。然而现实中常有不满足于PH假设的情况。如文章:All-cause and cause-specific mortality associated with diabetes in prevalent hemodialysis patients中报道了一个人的糖尿病状态可能会随着时间而变化,尿毒症患者肾功能随着时间变化加重,因此Cox 比例风险模型用在此处不合适,我们可以选用COX回归模型的扩展,一般有两种内在和外部,见下图
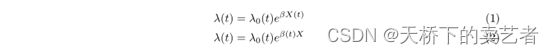
第一种我们可以看到时间t和X有关系,对系数β没什么影响,第二种可以看到时间t对β有影响,随着时间变化β是不同的,即系数是不同的。
对于第一种情况比较少见,今天我们主要来聊聊第二种情况,系数β随时间变化的cox时变系数模型(什么叫法都有,原理大概就是这个意思),使用的是survival包自带的肺癌数据集,我们先导入R包和数据
library(survival)
lung<-lung
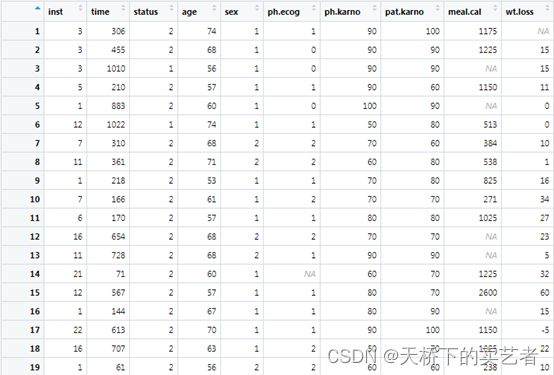
我们先来看一下数据,inst机构代码,time以天为单位的生存时间,status:结局变量,1为死亡0为存活,age: 年龄,sex: 男=1 女=2,ph.ecog: 由医师评定的 ECOG 表现评分。 0 = 无症状,1 = 有症状但完全不卧床,2 = 卧床时间 < 50%,3 = 卧床时间 > 50% 但不卧床,4 = 卧床,ph.karno: 由医师评定的 Karnofsky 表现评分(差=0-好=100),pat.karno: 由患者评定的 Karnofsky 性能评分,meal.cal: 用餐时消耗的卡路里,wt.loss: 过去六个月的体重减轻(磅)
我们先来拟合一个cox模型
fit2 <- coxph(Surv(time, status) ~age +ph.karno+sex,data=lung)
survival包自带的cox.zph函数可以用于PH假设的检查
zph <- cox.zph(fit2)
zph

我们可以看到ph.karno的P值小于0.05,表明ph.karno没有通过PH假设,全局显着性检验给出的 P 值 (0.0157) 表明模型缺乏拟合。我们可以通过plot函数对ph.karno这个变量进行可视化
plot(zph[2],lwd=2)
abline(0,0, col=1,lty=3,lwd=2)
abline(h= fit2$coef[2], col=3, lwd=2, lty=2)
legend("bottomright",
legend=c('Reference line for null effect',
"Average hazard over time",
"Time-varying hazard"),
lty=c(3,2,1), col=c(1,3,1), lwd=2)
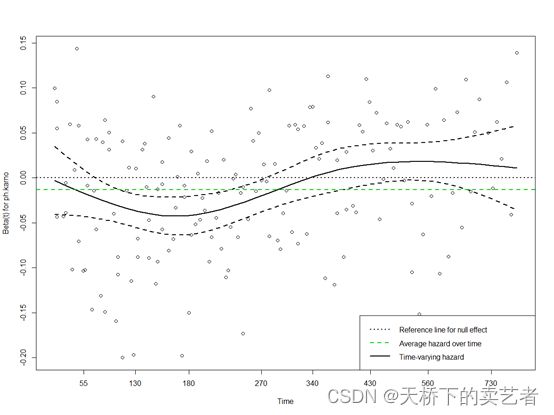
其中黑色虚线表示系数为0,就是ph.karno无效的情况,绿色虚线表示的是ph.karno的平均效应值,我们可以看到均线和实际背离是相当大的,因此这个情况使用cox.zph 函数来处理是非常恰当的。
对时变系数建模的一种方法是使用阶跃函数,例如 (g(t) = I ( t ≥ t o )),其中t o是指定值。这种方法的想法是将分析时间分成几个区间,并为这些时间区间分层 Cox 比例模型。随着时间的推移,固定基线协变量的影响会变得更强或更弱,这可以通过时间分层来探索。我们可以看到ph.karno大约在180和350左右有两个转折,我们可以使用survSplit函数进行分段,
lung.split <- survSplit(Surv(time, status) ~ .,
data= lung, cut=c(180, 350),
episode= "tgroup", id="id")
这样我们就多了一个新指标tgroup,如下图
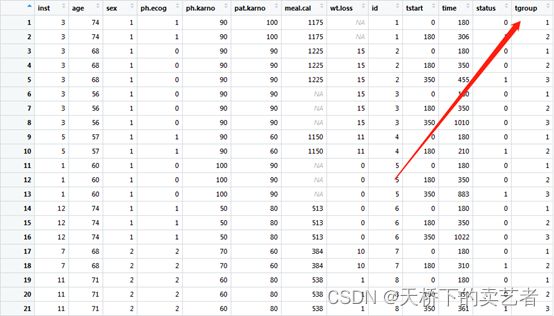
新指标tgroup对time的时区进行了划分,被分割成 (0, 180), (180, 350) 和 (350, 455) 的区间,tgroup=1 标识第一个时间间隔(0, 180),tgroup=2 标识第二个时间间隔(180, 350),3就是(350, 455)
现在我们把lung.split这个数据拿来重新进行模型拟合,建立一个ph.karno和tgroup的交互分层
fit.split <- coxph(Surv(tstart, time, status) ~
age + ph.karno:strata(tgroup)+
sex,
data=lung.split)
fit.split

我们可以看到tgroup=1的时候ph.karno是P是有意义的,HR=0.965594,其他时候就不行了,我们从新使用cox.zph函数进行PH假设评估
cox.zph(fit.split)

这次全部通过PH假设了,GLOBAL=0.2(大于0.05)表明模型是拟合的。
另一种方法是通过使用用户指定的参数连续函数来构造一个交互项,在 coxph() 函数中,有一个tt参数来指定时间的具体变换。在本例中,tt函数定义为“tt = function(x, t, …) x * log(t+20)”,其中 x 是具有时变效应的固定协变量,t是分析时间。tt() 函数应用于变量ph.karno。模型公式中的karno为“tt(ph.karno)”,为什么是log(t+20),依据参考文献的说法是选择在log(t+20)之上用cox.zph图的时间尺度,使得该图的前200天大致呈线性。
fit.tt <- coxph(Surv(time, status) ~
age + ph.karno + tt(ph.karno)+ sex,
data=lung,tt = function(x, t, ...) x * log(t+20))
fit.tt

ph.karno 和 tt(ph.karno) 的系数都具有统计显着性,这意味着 ph.karno 的影响随时间而变化。ph.karno 的时变效应可以写为 β(t) = -0.098+0.015×log( t + 20)。
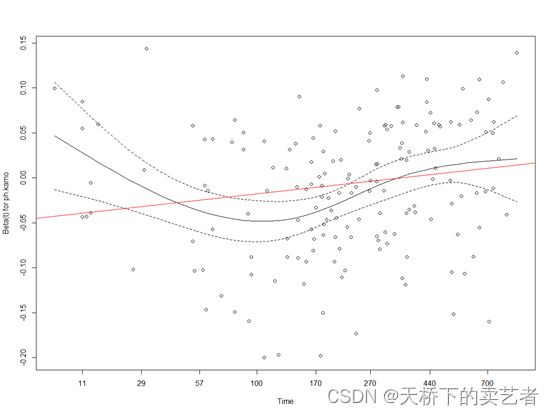
我们可以使用 abline() 函数在 ph.karno 对生存的时变影响的 cox.zph 图中添加一条线。
zph.tt <- cox.zph(fit2,
transform=function(t) log(t+20))
plot(zph.tt[2])
abline(coef(fit.tt)[2:3], col=2)
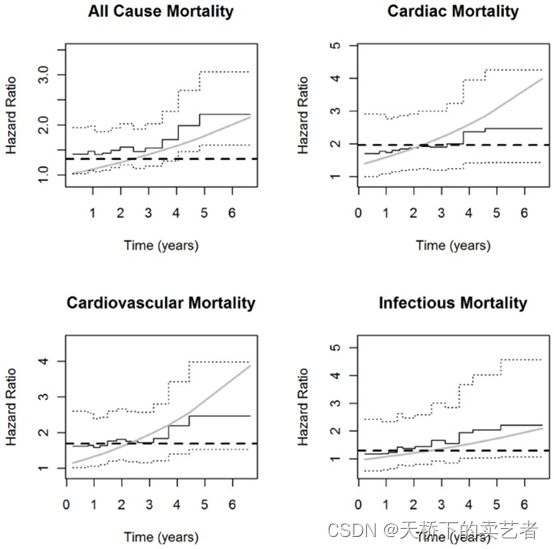
在有些文章中使用的是HR并非系数(如下图),如文章:All-cause and cause-specific mortality associated with diabetes in prevalent hemodialysis patients
我们也可以转换一下
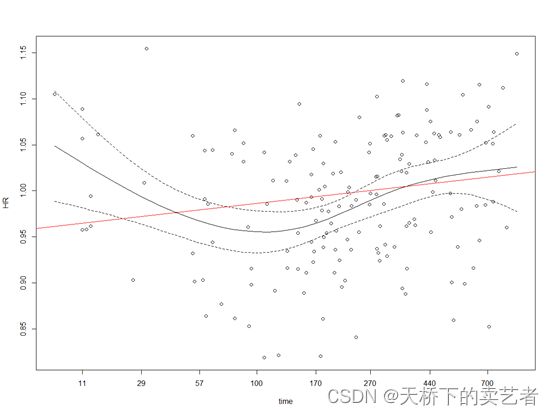
也可以添加一条有意义的参考线,至于什么是有意义的需要你自己研究了
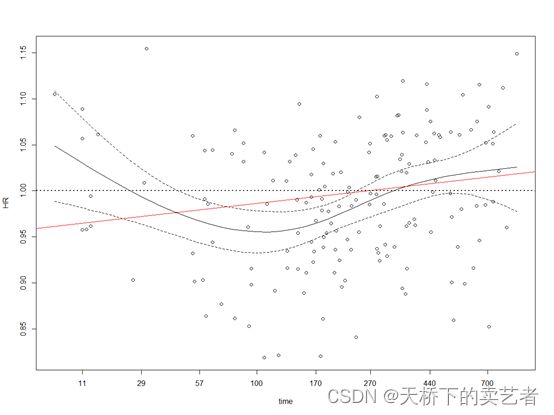
我们也可以使用timereg 包研究时变系数,timereg包附带的 timecox() 函数能够拟合具有时间固定和时变系数的 Cox 模型。时变效应通过重采样方法进行测试,想了解原理的请看参考文献。
library(timereg)
fit.out <- timecox(Surv(time,status)~
age+sex+ph.karno,
data=lung,n.sim=500,
max.time=700)
summary(fit.out)

输出的第一个表显示了非显着效应检验的结果(例如,原假设表明被检验的系数与 0 没有显着差异),这表明sex和ph . karno对生存结果有显着影响。第二个表显示了时间不变效应的检验。Kolmogorov-Smirnov 检验和 Cramer von Mises 检验都用于检验时不变效应,ph.karno 的效果不是固定时间的。
par(mfrow=c(2,2))
plot(fit.out)
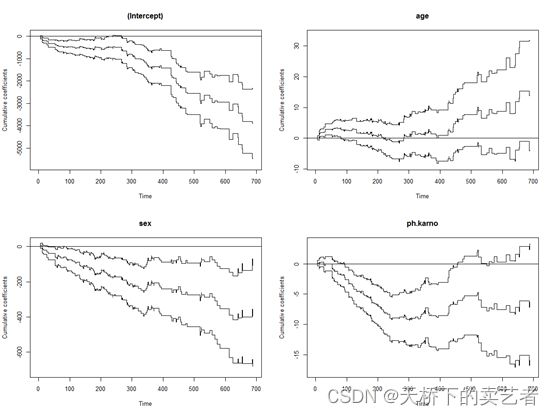
ph.karno在开始时很陡,然后在大约 250 之后变平。变量年龄没有显着影响,因为置信区间与零效应参考线相交。变量性别有显着影响,但不能拒绝时不变效应的原假设。通过 const() 函数将性别和年龄设置为时间固定效应变量。
fit.const <- timecox(Surv(time,status)~
const(age)+const(sex)+ph.karno,
data=lung,n.sim=500,
max.time=700)
summary(fit.const)
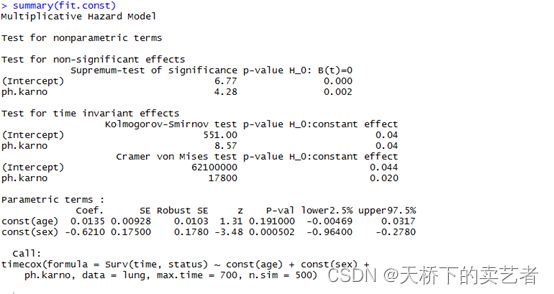
年龄和性别的常数效应分别为 0.0135 和 -0.6210。
par(mfrow=c(1,2))
plot(fit.const)
- Thomas L, Reyes EM. Tutorial: Survival Estimation for Cox Regression Models with Time-Varying Coefficients Using SASand R. Journal of Statistical Software 2014;61:1-23. 10.18637/jss.v061.c01
- Terry Therneau, Cynthia Crowson, Elizabeth Atkinson. Using Time Dependent Covariates and Time Dependent Coecients in the Cox Model. November 26, 2018
- Gray’s Time-Varying Coefficients Model for Posttransplant Survival of Pediatric Liver Transplant Recipients with a Diagnosis of Cancer
- Zhang Z, Reinikainen J, Adeleke KA, Pieterse ME, Groothuis-Oudshoorn CGM. Time-varying covariates and coefficients in Cox regression models. Ann Transl Med. 2018 Apr;6(7):121. doi: 10.21037/atm.2018.02.12. PMID: 29955581; PMCID: PMC6015946.
- Tian L, Zucker D, Wei LJ. On the Cox Model With Time-Varying Regression Coefficients. Harvard University Biostatistics Working Paper 2005;100:172-83.
- Adeleke KA, Abiodun AA, Ipinyomi RA. Semi-parametric non-proportional hazard model with time varying covariate. Womens Health Journal 2015;14:68-87
- Ren Y, Chang CC, Zenarosa GL, Tomko HE, Donnell DM, Kang HJ, Roberts MS, Bryce CL. Gray’s time-varying coefficients model for posttransplant survival of pediatric liver transplant recipients with a diagnosis of cancer. Comput Math Methods Med. 2013;2013:719389. doi: 10.1155/2013/719389. Epub 2013 May 12. PMID: 23762197; PMCID: PMC3665233.
- Sattar A, Argyropoulos C, Weissfeld L, Younas N, Fried L, Kellum JA, Unruh M. All-cause and cause-specific mortality associated with diabetes in prevalent hemodialysis patients. BMC Nephrol. 2012 Oct 1;13:130. doi: 10.1186/1471-2369-13-130. PMID: 23025844; PMCID: PMC3519533.