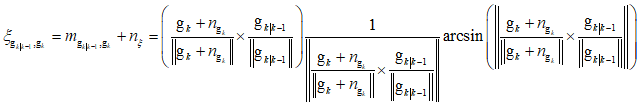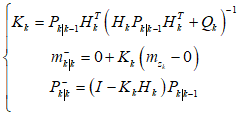Google Cardboard的九轴融合算法——基于李群的扩展卡尔曼滤波

Google Cardboard的九轴融合算法

——基于李群的扩展卡尔曼滤波

极品巧克力

 

前言

九轴融合算法是指通过融合IMU中的加速度计（三轴）、陀螺仪（三轴）、磁场计（三轴），来获取物体姿态的方法。它是开发VR头显中的一个至关重要的部分。VR头显必须要实时准确地获取用户头部的姿态，然后在屏幕上渲染出在对应的姿态所应该要看到的画面，才能让用户在VR世界里获得沉浸感。

因为人眼是非常精密的器官，如果渲染出来的画面稍微有一点点的延时或者偏差，人眼都能察觉出来，导致用户头晕想吐，再也不相信VR了。所以，VR头显对九轴融合算法的实时性和精度提出了非常高的要求。

而另一方面，公开的九轴融合方法又少之又少，常见的就是互补滤波算法和Madgwick算法，但是这两个方法的精度都不能达到VR头显的要求。而精度高的九轴融合算法都掌握在一些算法公司手里，需要向他们支付高昂的算法使用费，源码的价格更是天价。

Cardboard是谷歌在2014年发布的VR盒子，虽然它不是开源的，但是在GitHub上有很多Cardboard的反编译工程，比如https://github.com/rsanchezsaez/cardboard-java。Cardboard的VR体验，可以在一定程度上，证明它的九轴融合算法是满足VR要求的。所以，我对Cardboard反编译工程中的九轴融合部分的程序进行了研读，这部分的程序大概有5000行左右。我在通读完程序之后，结合文献[1],把程序背后的算法理论公式全部都反推出来，总结成了本文，与各位分享。

虽然早在2014年，Cardboard就已经在GitHub上被反编译了，但是这么多年过去了，有关它的代码原理分析的文章却是几乎没有。能结合源代码，把它背后的算法理论基础详细推导出来的，本文应该算是第一篇。如有推导错误的地方，还请各位不吝赐教。

本文目标读者：传感器融合算法工程师。

一.预测

基于陀螺仪积分来预测出下一个姿态。

假设在时刻的状态的SO3形式的概率满足高斯分布，

其中为归一化常数。为方便起见，把满足上面条件的表示成，。

在时刻，陀螺仪的测量值为，如果没有噪声的话，则对下一个时刻的状态均值的预测为，

其中，为时刻到时刻的时间间隔，。

而如果考虑噪声的影响的话，则对时刻的预测的状态分布要满足，

其中，表示陀螺仪数据的噪声，协方差可以通过采集一段时间的数据，计算得到。

所以，新的均值附近的扰动要满足这样的分布，

又因为有SO3上的性质，，所以，上式中的。所以，原式可以转换如下，

这时候，又因为有SO3上的伴随性质，

原式就可以转换为，

所以，就可以得到，

所以，新的扰动的均值，

新的扰动的协方差，，

所以，最终得到，

二.更新

设在世界坐标系下，加速度计所测的重力向量为，磁场计所测的磁场向量为。则在时刻时，加速度计所测的重力向量为，磁场计所测的磁场向量为。加速度计上面的测量噪声满足。磁场计上面的测量噪声。

2.1加速度计测量更新

把第一部分预测出来的姿态，作为预测的测量姿态，可以预测出当前加速度计的测量值，其计算过程如下，

而根据实际测量值，可以反过来计算出姿态，作为实际的测量姿态。以之前的预测姿态为初值，则把两者的关系表示为，

可以把优化出来，或者直接叉乘出来。

根据李代数与向量叉乘的转换关系。不考虑测量噪声，则可以得到的均值。

设上的噪声为，则关系满足如下，

进一步得到，

要获得与之间的关系，

这两者间的关系不是线性化的，那么就只能进行线性化，一阶泰勒展开，

其中，的计算，采用数值扰动的方法。

从而，可以得到。

最终得到，的分布，

再进行转换，用跟第一部分同样的方法，转换出扰动。

用来表示。

所以，根据第一部分，可以得到，现在又得到了。综合这两者的信息，可以得到，。就是要求一个，使得最大，用公式表达如下。

其中，是个未知数，用，转换成用未知数来表示。然后，上式就可以转换为，

但这样子也解不出来。对上式中的部分，在处进行线性化，一阶泰勒展开。则可以转换为，

其中，的计算，程序里面是用数值扰动的方法。这里应该也可以用解析的方法，把公式都展开来推导。

接下来，为了转换成卡尔曼滤波的形式，用来表示。

所以，原式就可以表示为，

参考《State Estimation for Robotics》的3.1.2和3.3.2，求，则上式最终可以转换出卡尔曼滤波的形式了。

所以，

同时，

则融合后的姿态的均值为，

设相对于姿态的李代数扰动。则与的关系要满足，

所以，得到扰动的均值，

得到扰动的协方差，

所以，的分布满足，

2.2公式总结

2.1中的公式总结出来就是，

上面的方法跟《State Estimation for Robotics》的7.3.4和8.2.4很像，但是上面的方法，对协方差的处理更加精细。

要融合磁场计，也是同样的方法。

要融合视觉SLAM中送过来的姿态，也是同样的方法。

3.实际程序

在cardboard的实际程序中，还有很多细节的处理。比如，

增加了很多加权滤波的方法。

把加速度计的模的变化滤波出来，实时更新加速度计的协方差。这一步，相当于是madgwick里面的动态调整权重，但这一步更好，因为是直接算加速度计的协方差来调整权重，而不是通过陀螺仪的测量值来间接表示运动过快而调整权重。

在静止的时候，把陀螺仪的偏移滤波出来。

还有时间差平滑滤波的方法。

在融合磁场计的时候，把磁场计向量映射到水平面上，相当于只优化水平面上的旋转偏差。这个，在空间想象时，应该保持重力竖直方向（0,0,1）不变，以此作为参考，再看原来的模型，就容易理解了。

 

但是没有对磁场计进行修正。如果要对磁场计进行修正，简单的方法可以参考madgwick里面的方法。全面的方法，则要参考那些专门搞磁场计标定的论文了。

4.总结

Cardboard里面的九轴融合算法，效果比Madgwick方法和互补滤波方法都要好，对细节的处理也非常棒。以后再写一篇文章，详细比较基于李群的扩展卡尔曼滤波方法，Madgwick算法，互补滤波的异同。

根据参考文献[1]，这套理论也同样可以使用在六自由度（位移+旋转）融合上面，只需要把SO3改成SE3就可以了。可以用同一套理论，把视觉SLAM的位姿与IMU位姿融合在一起，得到融合后的六自由度数据，应用在VR头显中。

希望有一天，VR头显的体验能做到像电影《头号玩家》里面那样。与仍然还在做VR的各位同行共勉。

5.求赞赏

您觉得，本文值多少？ 

6.有奖问答

给各位出一道思考题。

已知，一个IMU水平地放在桌面上不动。重力大小为。陀螺仪和加速度计以相同的频率同时输出，输出的时间间隔为。它的初始状态为。陀螺仪数据的噪声为，加速度计数据的噪声为。

其中，，，都为对角矩阵。则随着时间的增长，请问，

（1）这个IMU的后验状态协方差是否会收敛？

（2）如果收敛的话，会收敛到什么值？

请在下面评论区作答。第一名正确回答的，将可以获得哈士企公仔一只。

 

7.参考文献

 

1. Bourmaud G, Megret R, Giremus A, et al. Discrete Extended Kalman Filter on Lie groups[C]// Signal Processing Conference. EURASIP, 2013:1-5.
2. Timothy D. Barfoot. State Estimation for Robotics [M].Cambridge University Press, 2017.

 

 

 

 

转载于:https://www.cnblogs.com/ilekoaiq/p/8710812.html