信号的抽取

多速率信号处理

信号的抽取

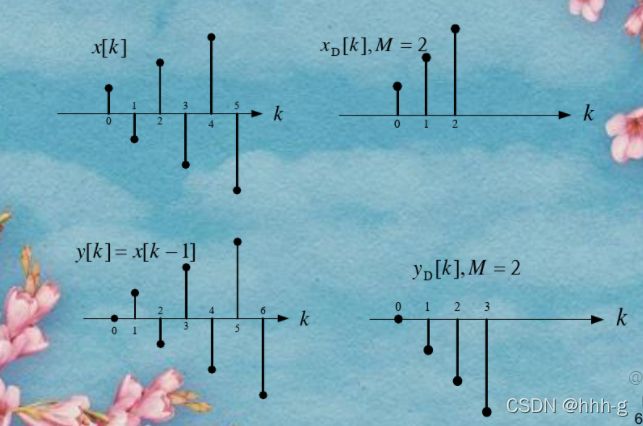
M倍抽取（down-sampler，M-fold decimator）

表示为：$\mathrm{y}[k]=x[Mk]$

例，2倍频抽取：

其中抽样系统为时变的，例：

利用MATLAB实现序列抽取：

N倍频抽取的变换域描述：

$y(n)=u(Nn)$，其中$y(n)$为抽取器的输出；

$Y(e^{jw})=\frac{1}{N}\sum _{k}U(e^{j\frac{w-2\pi k}{N}})$

$Y(z)=\frac{1}{N}\sum _{k}U(z^{\frac{1}{N}}{W}^k)$

其中 $u(n)\iff U(e^{jw})$，$u(n)\iff U(z)$。

证明：$y(n)\iff Y(z)$

${\delta }_N(n)=\sum _{r=-\infty }^{+\infty }\delta (n-rN)=\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j\frac{2\pi }{\text{N}}nk}$

$Y(z)=\sum _{n=-\infty }^{+\infty }y(n)z^{-n}=\sum _{n=-\infty }^{+\infty }u(Nn)z^{-n}$

$$\begin{gathered} =\sum _{n=-\infty , \\ n=iN}^{+\infty }u(n)z^{-\frac{n}{N}} \end{gathered}$$

$=\sum _{n=-\infty }^{+\infty }u(n){\delta }_N(n)z^{-\frac{n}{N}}$

$=\sum _{n=-\infty }^{+\infty }u(n)(\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j\frac{2\pi }{\text{N}}nk})z^{-\frac{n}{N}}$

$=\frac{1}{N}\sum _{k=0}^{N-1}(\sum _{n=-\infty }^{+\infty }u(n)e^{j\frac{2\pi }{\text{N}}nk}{z}^{-\frac{n}{N}})$

$=\frac{1}{N}\sum _{k=0}^{N-1}\left[\sum _{n=-\infty }^{+\infty }u(n){(e^{-j\frac{2\pi }{\text{N}}k}{z}^{\frac{1}{N}})}^{-n}\right]$

$=\frac{1}{N}\sum _{k=0}^{N-1}\left[\sum _{n=-\infty }^{+\infty }u(n){(W^k{z}^{\frac{1}{N}})}^{-n}\right]$

$=\frac{1}{N}\sum _{k=0}^{N-1}U(W^k{z}^{\frac{1}{N}})$

所以，$Y(z)=\frac{1}{N}\sum _{k}U(z^{\frac{1}{N}}{W}^k)$，证毕！
参考原文为：多速率信号处理基础