基于感知器的手写数字识别

1原理介绍

本次实验要求使用线性分类器实现手写数字识别，线性分类器选择的是感知器模型。基于感知器的实验数据必须是线性可分的，感知器不仅可以使用在二分类还可以使用在多分类。不过，在二分类与多分类的算法实现过程略有不同。这些不同主要体现在权重更新与判别超平面的实现两个方面。

1.1二分类

将数据分为两类。首先，要求数据是线性可分的；然后，选择初始权重，通过训练集实现对权重的更新；接着，使用更新后的权重实现对测试集的识别；最后，将识别结果与测试数据的标签进行比较，得出正确率。
上面是感知器的损失函数，该损失函数表示误分类点到判别超平面的距离，感知器算法通过更新权重实现损失函数的最小化。权重的更新规则：

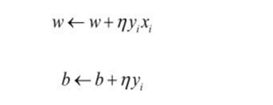
本次实验初始权重取0向量，b的取1向量。首先，判断某点到判别面的距离，计算yi*（wixi+b）是否大于0，该点被正确分类时，其wixi+b与yi是同号的，此时前面的计算式大于0；误分类时它们异号，前面的计算式小于0，此时需要对权重和b进行更新，已使yi*（wixi+b）大于0（注意：在初始权重下每个yi（wixi+b）都为0，此时认为每个点都是误分类点，然后一次更新权重）；接着，再次计算yi（wixi+b）是否大于0，如果大于零就去判断下一个点，否则就再次更新权重与b，直到对所有的点都有yi（wi*xi+b）。
感知器得到的判别超平面并不是唯一的，它与初值的选择以及迭代过程中误分类点的选择顺序都有很大关系，所以为了得到唯一的超平面，需要对分离超平面增加约束条件，这就形成了支持向量机。

1.2多类情况

本次实验使用感知器实现手写数字识别属于多分类的问题。首先对手写数字图片进行处理，将图片转化为88的01矩阵；然后，将该矩阵转化为一维数组的形式，X={x1,x2,…x64}，此时为了简化计算，将b并入权重向量W={b,w1,w2,…,w64}，因此需要在X前面加上1，计算wixi+b就简化为计算W.TX；然后，设置10组初始权重（因为数字为0-9，有10个类别），并对某个点一次用10组权重计算W.TX，得到10个目标函数值，使用argmax函数得到最大函数值对应的索引号，此索引号的值就是该决策识别的数字类别；接着，将识别到的值与该测试数据所对应的类别进行比较，如果两者相等说明识别正确，否则就需要对权重进行更新，并再次判断识别结果的正确性。
多类问题的权重更新与二分类有所不同，以下是多类问题权重的更新规则：

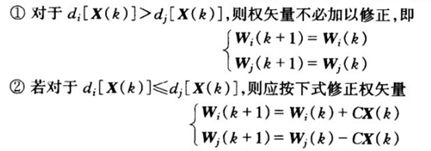
如，对于第j类的数据Xi，计算Wj.TXi，然后将其值与{W0.TXi,W1.TXi,W2.TXi,…,Wj-1.TXi,Wj+1.TXi,…,W9.TXi}逐个进行比较，如果Wj.TXi较大则与下一个进行比较，否则就需要对权重进行修正，C为学习率。直到Wj.TXi为10组权重向量中的最大值。这是多类问题与二分类问题再权重更新的不同，同时多类问题的判别超平面的实现也有差别，一般通过Wi.TXi-Wj.TXj=0得到第i个类别与第j个类别的超平面函数。

2代码

2.1代码介绍

下面给出了基于感知器的多分类问题的代码。整个代码分为数据预处理、确定初始权重、训练数据及更新权重以及识别数据几个部分。数据处理的代码就不列出来了，最后转化为1*65（在由64个特征构成的向量前面加1）的一维数组就行。

wk=[None for i in range(0,10)]
for i in range(0,10):#确定初始权重，这里将初始权重都设置为0向量
    wk[i]=np.zeros((65,1)).reshape((1,-1))
    # wk[i]=np.full(65,i).reshape(1,-1)
a=0.02#学习率
def circle(x,w1,w2):#更新权重，实现权重更新过程中的迭代
    distinguish_fun1=np.dot(x,w1)
    distinguish_fun2=np.dot(x,w2)
    count=0
    while(distinguish_fun1<=distinguish_fun2):#当Wj.T*Xi不大于其他组权重与Xi的内积时，进行循环
        w1=w1+np.dot(a,x)#更新Wj
        w2=w2-np.dot(a,x)#更新Wt
        count+=1#记录迭代次数
        distinguish_fun1=np.dot(x,w1)#计算更新后的Wj.T*Xi与Wt.T*Xi
        distinguish_fun2=np.dot(x,w2)
    return distinguish_fun1,count,w1,w2   #函数返回值
count_test = 0
for j in range(0,10):#测试集类别
    for i in range(j*37,j*37+37):#每个类别的样本
        wx=[]#存放Wt.T*Xi的值
        # wx1=[]
        for t in range(0,10):
            wx.append(np.dot(x0[i][0],wk[t][0]))
            # wx.append(np.dot(y0[i][0],wk[t][0]))
        label=np.argmax(wx)#返回识别的类别
        if label!=j:#不一致，需要进行权重修正
            for t1 in range(0,10):#遍历每组权重
                x,y,z,k=circle(x0[i][0],wk[j][0],wk[t1][0])
                wk[j][0]=z #将修改后的权重更新到Wj
    # print(f"权重向量为：{wk[j][0]}")
    for p in range(j*10,j*10+10):#将修正后的Wj作为识别第j类测试数据集的权重
        wx1=[]
        for t2 in range(0,10):#遍历每组权重
            wx1.append(np.dot(y0[p],wk[t2][0]))
        label1=np.argmax(wx1)
        if label1==j:
            count_test+=1
            print(f"待识别数字为{j};识别结果为{label1};识别正确")
        else:
            print(f"待识别数字为{j};识别结果为{label1};识别错误")
rate=count_test/100
print(f"正确率：{rate*100}%")
print(f"更新后的10组权重向量为：")

2.2结果分析

下图是得到的识别结果

最后结果的正确率为99%，符合实验的准确率要求。可以看出，感知器在多类问题的表现较为可观。