模型中出现欠拟合与过拟合的应对策略

        在训练模型的过程中，可能出现欠拟合(underfitting)或者过拟合(overfitting)，欠拟合：模型无法得到一个很小的训练误差，过拟合：训练误差不错，但测试误差比较大，或者说训练误差远小于测试误差，模型的泛化能力差。
        出现这两种情况的主要原因在于模型的复杂度与训练数据集的大小。现在我们使用多项式函数来解释模型复杂度，如果这个模型复杂度过低(比如线性函数)，容易出现欠拟合，如果复杂度过高，又会出现过拟合，所以需要选择一个合适复杂度的模型。
        我们来看下K阶多项式函数的数学表达式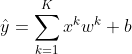： 如果K=1，就变成了一阶多项式函数，也就是线性函数。
        对于训练数据集，如果样本数过少，尤其是比模型参数的数量少很多的时候，很容易出现过拟合， 所以我们一般都需要训练比较大的数据集。

模型复杂度对欠拟合和过拟合的影响 

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd,gluon,nd
from mxnet.gluon import data as gdata,loss as gloss,nn

#y=1.2x-3.4x²+5.6x³+5+ε，其中ε是噪声
n_train,n_test,true_w,true_b=100,100,[1.2,-3,4,5.6],5
features=nd.random.normal(shape=(n_train+n_test,1))#(200,1)#线性
poly_features=nd.concat(features,nd.power(features,2),nd.power(features,3))#多项式形状(200,3)
labels=(true_w[0]*poly_features[:,0] + true_w[1]*poly_features[:,1]+true_w[2]*poly_features[:,2]+true_b)#参数增多了(权重与偏置)
labels+=nd.random.normal(scale=0.1,shape=labels.shape)#加个噪声
#print(features[:2],poly_features[:2],labels[:2])
'''
[[0.13271435]
 [1.0078678 ]]
 
[[0.13271435 0.0176131  0.00233751]
 [1.0078678  1.0157975  1.0237896 ]]
 
[5.049143 7.190733]

'''


#定义一个画图函数(y轴为对数尺度)[在d2l包中已存在]
def semilogy(x_vals,y_vals,x_label,y_label,x2_vals=None,y2_vals=None,legend=None,figsize=(5,4)):
    d2l.set_figsize(figsize)
    d2l.plt.xlabel(x_label)
    d2l.plt.ylabel(y_label)
    d2l.plt.semilogy(x_vals,y_vals)
    if x2_vals and y2_vals:
        d2l.plt.semilogy(x2_vals,y2_vals,linestyle='-.')
        d2l.plt.legend(legend)

#拟合数据集，观察不同复杂度对模型的影响
num_epochs,loss=100,gloss.L2Loss()
def fit_and_plot(train_features,test_features,train_labels,test_labels):
    net=nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize()
    batch_size=min(10,train_labels.shape[0])
    train_iter=gdata.DataLoader(gdata.ArrayDataset(train_features,train_labels),batch_size,shuffle=True)
    trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.01})
    train_ls,test_ls=[],[]
    for _ in range(num_epochs):
        for X,y in train_iter:
            with autograd.record():
                l=loss(net(X),y)
            l.backward()
            trainer.step(batch_size)
        train_ls.append(loss(net(train_features),train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),test_labels).mean().asscalar())
    print('最后一次迭代结果：训练损失',train_ls[-1],'测试损失',test_ls[-1])
    semilogy(range(1,num_epochs+1),train_ls,'epochs','loss',range(1,num_epochs+1),test_ls,['train','test'])
    print('权重值:',net[0].weight.data().asnumpy(),'\n偏差值:',net[0].bias.data().asnumpy())
    

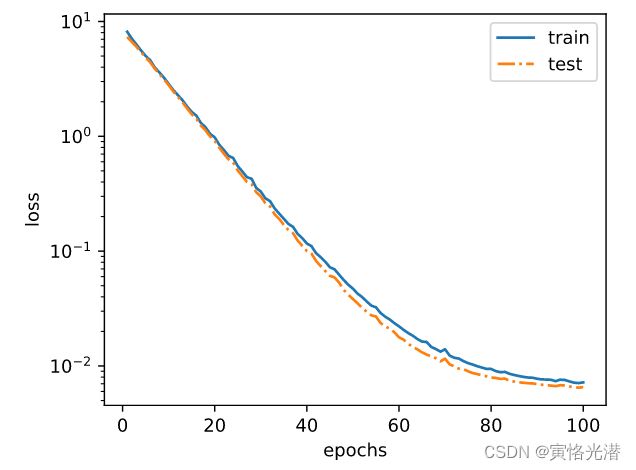
正常拟合

fit_and_plot(poly_features[:n_train,:],poly_features[n_train:,:],labels[:n_train],labels[n_train:])
最后一次迭代结果：训练损失 0.0055423467 测试损失 0.006460184
权重值: [[ 1.1825476 -2.9724765  3.9992456]] 
偏差值: [4.9615808]

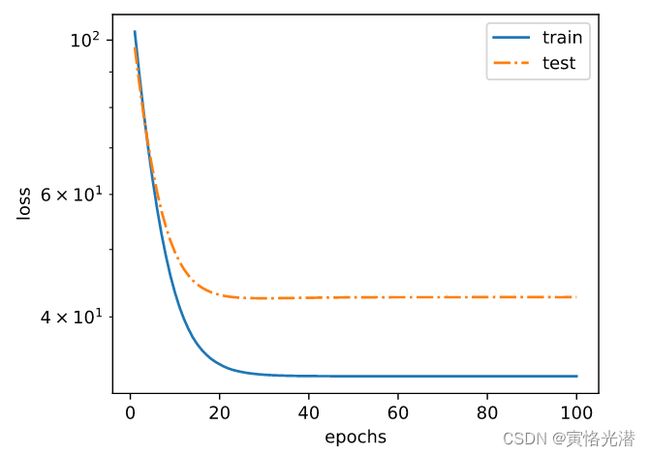
可以看出和真实权重值：1.2,-3.4,5.6以及偏差值：5相比较还是很接近的

欠拟合（线性函数）
fit_and_plot(features[:n_train,:],features[n_train:,:],labels[:n_train],labels[n_train:])
最后一次迭代结果：训练损失 32.87164 测试损失 42.70703
权重值: [[12.730066]] 
偏差值: [1.2960923]

        该模型在早期可以看到损失值降低之后就基本没有降低了，最后一次的迭代结果也看的出，损失误差还是很大，说明线性模型在非线性模型（如本例的三阶多项式函数）生成的数据集上容易欠拟合

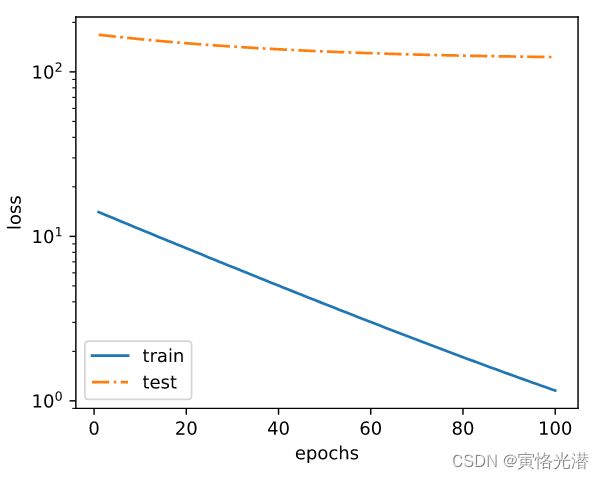
过拟合（样本数少）
fit_and_plot(poly_features[:2,:],poly_features[n_train:,:],labels[:2],labels[n_train:])
最后一次迭代结果：训练损失 1.1543251 测试损失 123.07513
权重值: [[0.8218897  1.1145158  0.79218584]] 
偏差值: [3.0100925]

        训练的样本数量很少，造成训练的误差小，但是在测试的时候，发现误差特别大，这就是泛化能力太差。也就是说样本数量远小于模型参数的数量了，显得模型就特别复杂，在训练过程中容易受到噪声的影响。
        对于欠拟合主要就是模型复杂度太小引起的，比如线性函数，所以选择合适的模型即可，对于过拟合常见的处理方法有权重衰减和丢弃法。

权重衰减(L2范数正则化regularization)

        针对数据样本少容易出现过拟合，如果获取训练数据的成本比较高，这个时候可以使用权重衰减(weight decay)，通过为模型损失函数添加惩罚项，是的学出的模型参数较小，也就是减小了模型的复杂度，来应对过拟合。有兴趣的还可以参阅：抑制过拟合的方法之权值衰减

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd,gluon,init,nd
from mxnet.gluon import data as gdata,loss as gloss,nn

#使用高维线性回归来模拟过拟合，特意将训练样本数设得很小：20
n_train,n_test,num_inputs=20,100,200
true_w,true_b=nd.ones((num_inputs,1))*0.01,0.05
features=nd.random.normal(shape=(n_train+n_test,num_inputs))
labels=nd.dot(features,true_w)+true_b
labels+=nd.random.normal(scale=0.01,shape=labels.shape)
train_features,test_features=features[:n_train,:],features[n_train:,:]
train_labels,test_labels=labels[:n_train],labels[n_train:]

#初始化模型参数，并附上梯度
def init_params():
    w=nd.random.normal(scale=1,shape=(num_inputs,1))
    b=nd.zeros(shape=(1,))
    w.attach_grad()
    b.attach_grad()
    return [w,b]

#定义L2范数惩罚项
def l2_penalty(w):
    return (w**2).sum()/2

batch_size,num_epochs,lr=1,100,0.003
net,loss=d2l.linreg,d2l.squared_loss#线性回归，平方损失
train_iter=gdata.DataLoader(gdata.ArrayDataset(train_features,train_labels),batch_size,shuffle=True)

#λ为0不使用权重衰减，也就是模拟过拟合
def fit_and_plot(lambd):
    w,b=init_params()
    train_ls,test_ls=[],[]
    for _ in range(num_epochs):
        for X,y in train_iter:
            with autograd.record():
                l=loss(net(X,w,b),y) + lambd*l2_penalty(w)#添加惩罚项
            l.backward()
            d2l.sgd([w,b],lr,batch_size)
        train_ls.append(loss(net(train_features,w,b),train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features,w,b),test_labels).mean().asscalar())
    d2l.semilogy(range(1,num_epochs+1),train_ls,'epochs','loss',range(1,num_epochs+1),test_ls,['train','test'])
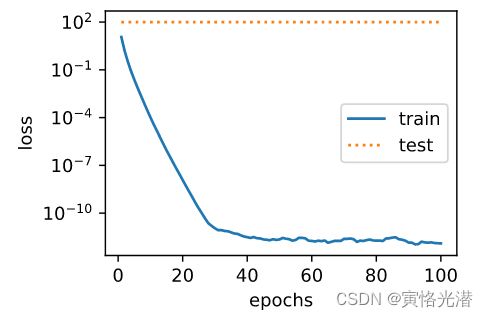
    print('L2权重的范数：',w.norm().asscalar())

原始的线性函数（过拟合）
fit_and_plot(0)
L2权重的范数： 14.131355

​

使用惩罚项来抑制过拟合
fit_and_plot(3)
L2权重的范数： 0.040131252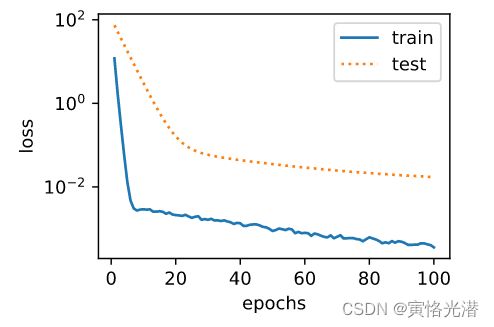
​
        大家可以把λ调大调小（大于0的超参数），看下有什么变化，可以知道这个常数λ是用来平衡这个新的额外惩罚的损失的，λ越大对权重的约束就越大，从下面的公式也可以看出，目的就是让权重缩小到0，所以也是为什么叫做权重衰减的原因了。

 ​

 Gluon简洁实现

batch_size,num_epochs,lr=1,100,0.003
def fit_and_plot_gluon(wd):
    net=nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize(init.Normal(sigma=1))
    #对权重做衰减，权重名称一般以weight结尾
    train_w=gluon.Trainer(net.collect_params('.*weight'),'sgd',{'learning_rate':lr,'wd':wd})
    #对偏差不做衰减
    train_b=gluon.Trainer(net.collect_params('.*bias'),'sgd',{'learning_rate':lr})
    train_ls,test_ls=[],[]
    for _ in range(num_epochs):
        for X,y in train_iter:
            with autograd.record():
                l=loss(net(X),y)
            l.backward()
            train_w.step(batch_size)
            train_b.step(batch_size)
        train_ls.append(loss(net(train_features),train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),test_labels).mean().asscalar())
    d2l.semilogy(range(1,num_epochs+1),train_ls,'epochs','loss',range(1,num_epochs+1),test_ls,['train','test'])
    print('L2范数的权重值:',net[0].weight.data().norm().asscalar())

丢弃法(Dropout)

        有兴趣的可以参阅以前的一篇文章：抑制过拟合的方法之Dropout(随机删除神经元)，丢弃法也是经常用来抑制过拟合常见的方法，将隐藏层的神经单元通过概率进行随机丢弃，这样的好处就是输出层的计算无法过度依赖隐藏层里的任意的神经单元，从而在训练模型中起到正则化的作用。

import d2lzh as d2l
from mxnet import autograd,gluon,init,nd
from mxnet.gluon import loss as gloss,nn

#drop_prob丢弃的概率
def dropout(X,drop_prob):
    keep_prob=1-drop_prob
    if keep_prob==0:
        return X.zeros_like()
    mask=nd.random.uniform(0,1,X.shape)return mask*X/keep_prob

num_inputs,num_outputs,num_hidden1,num_hidden2=784,10,256,256
W1=nd.random.normal(scale=0.01,shape=(num_inputs,num_hidden1))
b1=nd.zeros(num_hidden1)
W2=nd.random.normal(scale=0.01,shape=(num_hidden1,num_hidden2))
b2=nd.zeros(num_hidden2)
W3=nd.random.normal(scale=0.01,shape=(num_hidden2,num_outputs))
b3=nd.zeros(num_outputs)
params=[W1,b1,W2,b2,W3,b3]
for param in params:
    param.attach_grad()

#每个层的丢弃概率的设置：靠近输入层的一般设置小一点，另外测试的时候不需要使用丢弃法
drop_prob1,drop_prob2=0.2,0.5
def net(X):
    X=X.reshape((-1,num_inputs))
    H1=(nd.dot(X,W1)+b1).relu()
    if autograd.is_training():
        H1=dropout(H1,drop_prob1)#在第一层全连接后添加丢弃层
    H2=(nd.dot(H1,W2)+b2).relu()
    if autograd.is_training():
        H2=dropout(H2,drop_prob2)#在第二层全连接后添加丢弃层
    return nd.dot(H2,W3)+b3

#训练Fashion-MNIST数据集来测试丢弃法
num_epochs,lr,batch_size=5,0.5,256
loss=gloss.SoftmaxCrossEntropyLoss()
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)

 epoch 1, loss 1.1844, train acc 0.542, test acc 0.783
epoch 2, loss 0.5835, train acc 0.782, test acc 0.835
epoch 3, loss 0.4926, train acc 0.820, test acc 0.852
epoch 4, loss 0.4521, train acc 0.835, test acc 0.861
epoch 5, loss 0.4163, train acc 0.847, test acc 0.861

Gluon简洁实现

net=nn.Sequential()
net.add(nn.Dense(256,activation='relu'),nn.Dropout(drop_prob1),
       nn.Dense(256,activation='relu'),nn.Dropout(drop_prob2),nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))
trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':lr})
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,trainer)

出现的错误处理

Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.
Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.
Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.
Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.

对数的负数负号显示乱码，怎么正常显示这个负号呢？

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']#界面可带中文
plt.rcParams['axes.unicode_minus'] = False#正常显示负号

没起作用，然后在这位大神文章找了方法： matplotlib编码字体错误的解决过程
修改源码（地址因人而异）：D:\Anaconda3\envs\myd2l\Lib\site-packages\matplotlib\mathtext.py 
将UnicodeFonts类中_get_glyph方法中的fontname修改为it
或者TruetypeFonts类中_get_info方法中的fontname修改为it 

最后关于为什么使用L2范数，而不是L1范数？
        事实上，这个选择在整个统计领域中都是有效的和受欢迎的。L2正则化线性模型构成经典的岭回归（ridge regression）算法，  L1正则化线性回归是统计学中类似的基本模型， 通常被称为套索回归（lasso regression）。使用L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中，这可能使它们对单个变量中的观测误差更为稳定。 相比之下，L1惩罚会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零。 这称为特征选择（feature selection），这可能是其他场景下需要的。