MATLAB实例:PCA(主成成分分析)详解
发现一篇非常实用的pca matlab程序学习文章,包括对matlab自带的pca函数的解释说明,转载链接放到文末。另外整理了涉及到的一些其他内容一并放入文中
1. 主成成分分析
对于数学原理,可参见:CodingLabs - PCA的数学原理
本文不再赘述
2. MATLAB解释
详细信息请看:Principal component analysis of raw data - mathworks
[coeff,score,latent,tsquared,explained,mu] = pca(X)
coeff = pca(X) returns the principal component coefficients, also known as loadings, for the n-by-p data matrix X. Rows of X correspond to observations and columns correspond to variables.
The coefficient matrix is p-by-p.
Each column of coeff contains coefficients for one principal component, and the columns are in descending order of component variance.
By default, pca centers the data and uses the singular value decomposition (SVD) algorithm.
coeff = pca(X,Name,Value) returns any of the output arguments in the previous syntaxes using additional options for computation and handling of special data types, specified by one or more Name,Value pair arguments.
For example, you can specify the number of principal components pca returns or an algorithm other than SVD to use.
[coeff,score,latent] = pca(___) also returns the principal component scores in score and the principal component variances in latent.
You can use any of the input arguments in the previous syntaxes.
Principal component scores are the representations of X in the principal component space. Rows of score correspond to observations, and columns correspond to components.
The principal component variances are the eigenvalues of the covariance matrix of X.
[coeff,score,latent,tsquared] = pca(___) also returns the Hotelling's T-squared statistic for each observation in X.
[coeff,score,latent,tsquared,explained,mu] = pca(___) also returns explained, the percentage of the total variance explained by each principal component and mu, the estimated mean of each variable in X.
coeff: X矩阵所对应的协方差矩阵V的所有特征向量组成的矩阵,即变换矩阵或投影矩阵,coeff每列代表一个特征值所对应的特征向量,列的排列方式对应着特征值从大到小排序。
score: 表示原数据在各主成分向量上的投影。但注意:是原数据经过中心化后在主成分向量上的投影。score每行对应样本观测值,每列对应一个主成份(变量),它的行和列的数目和X的行列数目相同。
latent: 是一个列向量,主成分方差,也就是各特征向量对应的特征值,按照从大到小进行排列。( 简洁点说就是X 所对应的协方差矩阵的特征值,latent=diag(cov(score)))
tsquared: X中每个观察值的Hotelling的T平方统计量。Hotelling的T平方统计量(T-Squared Statistic)是每个观察值的标准化分数的平方和,以列向量的形式返回。(即用来衡量多变量间的距离,这个距离是指样本观测值到数据集中心的距离。)
explained: 由每个主成分解释的总方差的百分比,每一个主成分所贡献的比例。explained = 100*latent/sum(latent)。
mu: 每个变量X的估计平均值。
注:
自己手动编写PCA时,需要对数据进行中心化处理。矩阵中心化是使用数据减去数据的均值(每一列代表一个特征向量,计算出一个均值)
利用MATLAB自带函数计算PCA的时候,MATLAB自动对列进行了去均值的操作,但是并不对数据进行标准化,如果要标准化的话,用zscore函数,即x=zscore(X)。另外,如果直接有现成的协方差阵,用函数pcacov来计算。
若仍然对函数表示的信息不理解,可以参照:
(19条消息) matlab pca函数怎么用,matlab的pca函数说明_欧克米路的博客-CSDN博客
插入:矩阵的特征值与特征向量概念
假设我们有一个n阶的矩阵A以及一个实数λ,使得我们可以找到一个非零向量x,满足:
Ax=λx
如果能够找到的话,我们就称λ是矩阵A的特征值,非零向量x是矩阵A的特征向量。
对应在matlab中,即为eig函数:
[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V,其列是对应的右特征向量,使得 A*V = V*D。
可参考:(20条消息) 特征值分解:特征值,特征向量,特征向量矩阵_Nico的博客-CSDN博客_矩阵分解特征值和特征向量
eig和eigs的区别
d = eigs(A,k) % 返回一个向量,其中包含矩阵 A 的 k 个模最大的特征值(默认是6个)当使用 eig 计算所有特征值的计算量很大时(例如对于大型稀疏矩阵来说),这是非常有用的。
3. MATLAB程序
3.1 方法一:指定降维后低维空间的维度k
function [data_PCA, COEFF, sum_explained]=pca_demo_1(data,k)
% k:前k个主成分
data=zscore(data); %归一化数据
[COEFF,SCORE,latent,tsquared,explained,mu]=pca(data);
latent1=100*latent/sum(latent);%将latent特征值总和统一为100,便于观察贡献率
data= bsxfun(@minus,data,mean(data,1));
data_PCA=data*COEFF(:,1:k);
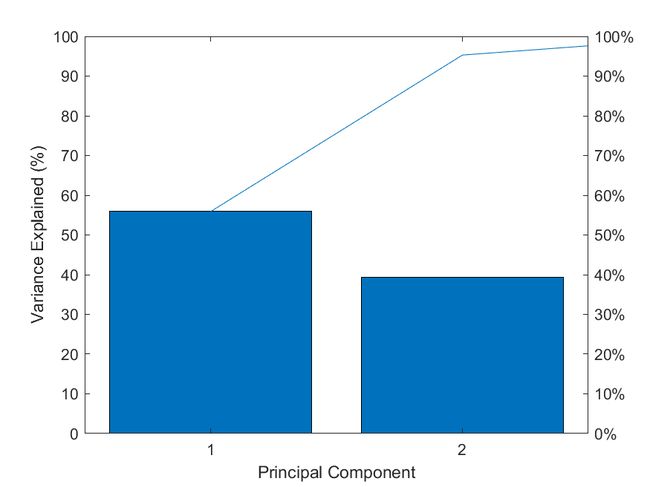
pareto(latent1);%调用matla画图 pareto仅绘制累积分布的前95%,因此y中的部分元素并未显示
xlabel('Principal Component');
ylabel('Variance Explained (%)');
% 图中的线表示的累积变量解释程度
print(gcf,'-dpng','PCA.png');
sum_explained=sum(explained(1:k));
end3.2 方法二:指定贡献率percent_threshold
function [data_PCA, COEFF, sum_explained, n]=pca_demo_2(data)
%用percent_threshold决定保留xx%的贡献率
percent_threshold=95; %百分比阈值,用于决定保留的主成分个数;
data=zscore(data); %归一化数据
[COEFF,SCORE,latent,tsquared,explained,mu]=pca(data);
latent1=100*latent/sum(latent);%将latent特征值总和统一为100,便于观察贡献率
A=length(latent1);
percents=0; %累积百分比
for n=1:A
percents=percents+latent1(n);
if percents>percent_threshold
break;
end
end
data= bsxfun(@minus,data,mean(data,1));
data_PCA=data*COEFF(:,1:n);
pareto(latent1);%调用matla画图 pareto仅绘制累积分布的前95%,因此y中的部分元素并未显示
xlabel('Principal Component');
ylabel('Variance Explained (%)');
% 图中的线表示的累积变量解释程度
print(gcf,'-dpng','PCA.png');
sum_explained=sum(explained(1:n));
end4. 结果
数据来源于MATLAB自带的数据集hald
>> load hald
>> [data_PCA, COEFF, sum_explained]=pca_demo_1(ingredients,2)
data_PCA =
-1.467237802258083 -1.903035708425560
-2.135828746398875 -0.238353702721984
1.129870473833422 -0.183877154192583
-0.659895489750766 -1.576774209965747
0.358764556470351 -0.483537878558994
0.966639639692207 -0.169944028103651
0.930705117077330 2.134816511997477
-2.232137996884836 0.691670682875924
-0.351515595975561 1.432245069443404
1.662543014130206 -1.828096643220118
-1.640179952926685 1.295112751426928
1.692594091826333 0.392248821530480
1.745678691164958 0.437525487914425
COEFF =
0.475955172748970 -0.508979384806410 0.675500187964285 0.241052184051094
0.563870242191994 0.413931487136985 -0.314420442819292 0.641756074427213
-0.394066533909303 0.604969078471439 0.637691091806566 0.268466110294533
-0.547931191260863 -0.451235109330016 -0.195420962611708 0.676734019481284
sum_explained =
95.294252628439153
>> [data_PCA, COEFF, sum_explained, n]=pca_demo_2(ingredients)
data_PCA =
-1.467237802258083 -1.903035708425560
-2.135828746398875 -0.238353702721984
1.129870473833422 -0.183877154192583
-0.659895489750766 -1.576774209965747
0.358764556470351 -0.483537878558994
0.966639639692207 -0.169944028103651
0.930705117077330 2.134816511997477
-2.232137996884836 0.691670682875924
-0.351515595975561 1.432245069443404
1.662543014130206 -1.828096643220118
-1.640179952926685 1.295112751426928
1.692594091826333 0.392248821530480
1.745678691164958 0.437525487914425
COEFF =
0.475955172748970 -0.508979384806410 0.675500187964285 0.241052184051094
0.563870242191994 0.413931487136985 -0.314420442819292 0.641756074427213
-0.394066533909303 0.604969078471439 0.637691091806566 0.268466110294533
-0.547931191260863 -0.451235109330016 -0.195420962611708 0.676734019481284
sum_explained =
95.294252628439153
n =
25. 参考
[1] 周志华,《机器学习》.
[2] MATLAB实例:PCA降维
MATLAB实例:PCA(主成成分分析)详解 - 凯鲁嘎吉 - 博客园 (cnblogs.com)