pytorch学习笔记-实践-RNN-sin预测cos
RNN 通过Sin预测Cos
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.animation #导入动图包
import math ,random
torch.__version__
'1.2.0'
在介绍循环神经网络时候我们说过,循环神经网络由于其的特殊结构,十分十分擅长处理时间相关的数据,下面我们就来通过输入sin函数,输出cos函数来实际使用。 首先,我们还是定义一些超参数
TIME_STEP = 10 #rnn时序步长(一个time的特征数量)
INPUT_SIZE = 1 #输入维度
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu") #是否使用GPU
H_SIZE = 64 # 隐藏单元个数
EPOCHES = 300 #总共训练次数
h_state = None #隐藏层状态
由于是使用sin和cos函数,所以这里不需要dataloader,我们直接使用Numpy生成数据,Pytorch没有π这个常量,所以所有操作都是用Numpy完成
steps = np.linspace(0,np.pi*2 , 256,dtype=np.float32) #在0-2pi之间形成相同间距的256个点
x_np = np.sin(steps)
y_np = np.cos(steps)
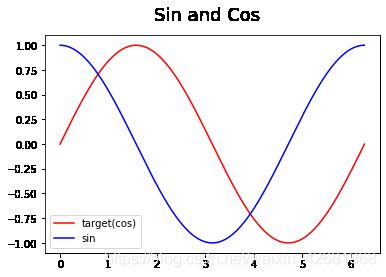
生成完之后可视化一下数据
plt.figure(1) #新建一个名叫 Figure1的画图窗口
plt.suptitle('Sin and Cos',fontsize='18') #设置标题
plt.plot(steps,x_np,'-r',label = 'target(cos)')
plt.plot(steps,y_np,'-b',label = 'sin')
plt.legend(loc='best')
plt.show()
下面定义一下网络结构
class RNN(nn.Module):
def __init__(self):
super(RNN,self).__init__()
self.rnn = nn.RNN( #rnn层
input_size = INPUT_SIZE,
hidden_size = H_SIZE,
num_layers = 1,
batch_first = True,
)
self.out = nn.Linear(H_SIZE,1) #输出函数,把64维数字转化为1维的
def forward(self,x,h_state):
# x (batch, time_step, input_size) ----(1,10,1)
# h_state (n_layers, batch, hidden_size) ----(1,1,64)
#虽然设置了batch_first ,但是h_n,c_n这些隐层状态的以一个仍然是layers
# r_out (batch, time_step, hidden_size) ----(1,10,64)
r_out,h_state = self.rnn(x,h_state)
outs = [] #保存所有预测值
for step in range(r_out.size(1)): #计算每一个步长的预测值
outs.append(self.out(r_out[:,step,:]))
return torch.stack(outs,dim=1) , h_state
下面定义损失和优化
rnn = RNN()
optimizer = optim.Adam(rnn.parameters()) # Adam优化,几乎不用调参
criterion = nn.MSELoss()
rnn.train()
plt.figure(2)
for step in range(EPOCHES):
start , end = step * np.pi , (step + 1) * np.pi #一个时间周期
steps = np.linspace(start,end,TIME_STEP,dtype=np.float32) #在这个周期内形成等间距的10个点
x_np = np.sin(steps) #此时size为(10,)
y_np = np.cos(steps)
x = torch.from_numpy(x_np[np.newaxis,:,np.newaxis]) #size(batch,time_step ,input_size) ,size变成1,10,1
y = torch.from_numpy(y_np[np.newaxis,:,np.newaxis])
#向前传播得到预测结果
prediction,h_state = rnn(x,h_state)
#重置隐藏层状态,切断和前一次迭代的连接
h_state = h_state.data
#损失函数
loss = criterion(prediction,y)
#梯度清零,损失回传,优化参数
optimizer.zero_grad()
loss.backward()
optimizer.step()
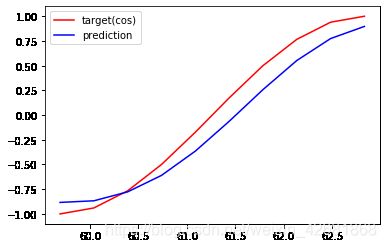
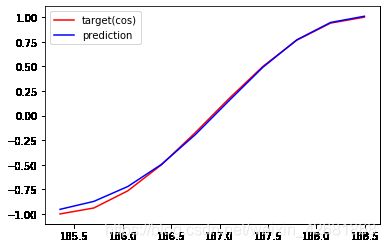
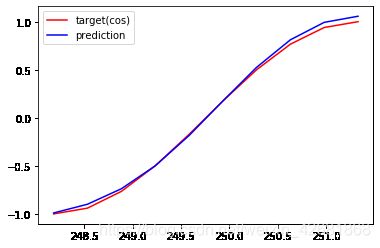
#可视化效果
if (step+1) % 20 ==0:
print("EPOCHS: {},Loss:{:4f}".format(step,loss))
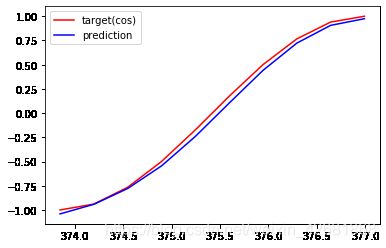
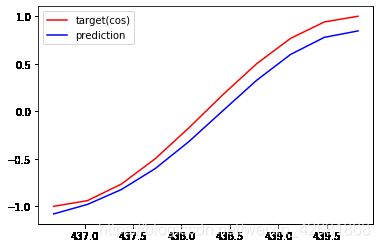
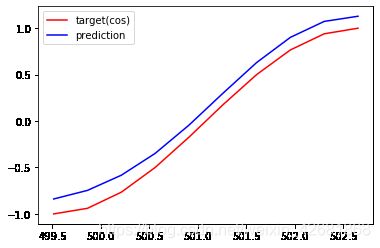
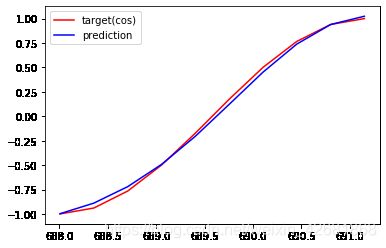
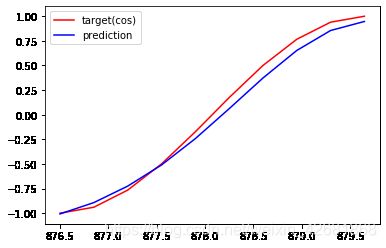
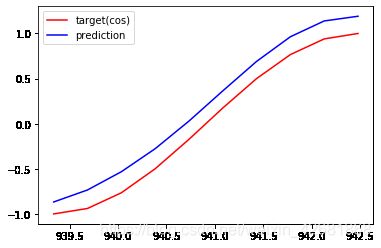
plt.plot(steps, y_np.flatten(), 'r-', label = 'target(cos)')
plt.plot(steps, prediction.data.numpy().flatten(), 'b-', label = 'prediction')
plt.legend(loc='best')
plt.draw()
plt.pause(0.01)
EPOCHS: 19,Loss:0.026650
EPOCHS: 39,Loss:0.015627
EPOCHS: 59,Loss:0.000972
EPOCHS: 79,Loss:0.001139
EPOCHS: 99,Loss:0.000598
EPOCHS: 119,Loss:0.002074
EPOCHS: 139,Loss:0.018051
EPOCHS: 159,Loss:0.022125
EPOCHS: 179,Loss:0.007365
EPOCHS: 199,Loss:0.005959
EPOCHS: 219,Loss:0.001204
EPOCHS: 239,Loss:0.001862
EPOCHS: 259,Loss:0.001517
EPOCHS: 279,Loss:0.006071
EPOCHS: 299,Loss:0.039190
发现训练效果还可以,但是最后损失反而变大了。应该做一个损失阈值,当损失足够小时就可以停止训练了。