最优传输论文(四)Deep multi-Wasserstein unsupervised domain adaptation

前言

代码见： https://github.com/namletien/mcda

在域适应过程中，标准泛化边界提示我们最小化三个项的总和:(a)源域真实风险，(b)源和目标域之间的散度，©两个域上理想联合假设的组合误差。
本文中提出MCDA方法——最小化前两项，同时控制第三项，从而解决忽略第三项带来的负迁移问题。MCDA受益于高度自信的目标样本(使用softmax预测)，以最小化按类别的Wasserstein距离，并有效地近似理想的联合假设。

图1 通用模型(左上)，模型MCDA(右上)和multi-critic(下)。
潜在空间是由名为特征提取器的神经网络学习的，它将源和目标样本作为输入，并输出潜在特征Zs,Zt，从而减少源和目标域之间的分歧。
无监督DA中，最小化潜空间中的分布离散度和源误差都是由泛化边界实现的，即 ∀h∈H，

要想学习一个有小的目标域误差 e t(h)的模型，三个元素需要小:
(a)源域真实误差e s(h)
(b)源域和目标域之间的分歧 d(Ps,Pt)
©两个域之间的理想联合假设 h* 的合并误差(通常称为λ)

特征提取器和分类器分别最小化两个分布和源误差，λ通常被认为是可以忽略的。
但对准源域和目标域并不一定意味着域的相应类也对准，负迁移通常发生在源域和目标域之间的差异太大而无法由DA过程补偿时。

本文的目标是考虑泛化边界中涉及的三个项，提出MCDA (Multi-Critic Domain Adaptation).
MCDA的目标是通过学习理想联合假设 h* 的近似值来控制λ项，并指导特征提取器最小化其相应的联合误差。由于无法获得标记的目标样本，我们用高置信度的目标样本。
我们不是只从标记的源样本中训练分类器，而是从源样本和高置信度目标样本中反复训练分类器，我们称之为混合分类器。该模型的好处是，从只有几个高置信度的目标样本开始，它调整自己以适应特定的目标特征，并平缓地忽略特定的源特征(因为特征提取器只能缓解但不能完全消除域迁移问题)，并准确地分类更多的目标样本，趋向于迭代地向理想的 h *移动。
本文使用了一种特殊的神经分支，称为multi-critic，它能够同时学习多个Wasserstein距离(图1，右上)。multi-critic受益于分类器的高精度，从而更好地对齐源类和目标类。总而言之，分类器和multi-critic都引导特征提取器最小化散度，同时最小化潜在空间中的联合误差(图1，下)。

background knowledge

wasserstein距离：

WGAN提出解决Kantorovich-Rubinstein对偶来代替：

f 为1-Lipschitz函数，即对任意x1,x2,满足
|f(x1)-f(x2)|<=|x1-x2|*1
学习 W (p1, p2)简单地归结为学习一个1- Lipschitz函数 f 最大化公式(3)，这可以通过一个称为critic的标准神经网络来完成, critic 包含几个(通常是两个)具有单个输出神经元的完全连接层，获取输入z∈Z并返回单个值 f(z)。
然而，在源和目标样本对之间的直线上的任意点上加单位梯度范数被证明是更有效的:

其中~P定义为沿着从数据p1和p2中采样的点对之间的直线均匀采样。

multi-critic domain adaption

Learning multiple Wasserstein distance

我们的目标是学习k + 1对分布在潜在空间Z上的Wasserstein距离:
其中一个在全局对(P s z,P t z),k个在类特定分布上(P si z,P ti z),i=1,…,k.我们学习了P si z和(戴帽)P ti z之间的Wasserstein 距离，(戴帽)P ti z是由混合分类器C对目标样本的softmax预测得到的。
需要注意critic不能同时学习两个不同的Wasserstein距离,为了克服这个问题，我们使用一个称为multi-critic的单一神经组件M，它能够并行学习k + 1个不同的距离(图1，下).

multi-critic将一个向量z作为输入，然后是一个与k + 1行的神经元矩阵全连接的层。然后，我们求助于一个局部连接层映射到k + 1个输出神经元。第i个输出神经元的任务是学习W (P si z,(戴帽)P ti z)，即对应于式(3)中的函数 f i。
由于我们学习了k + 1个不同的Wasserstein距离。它们遵循Eq.(3)中相应的期望，使得在multi-critic的第i个输出神经元遭受的损失为:

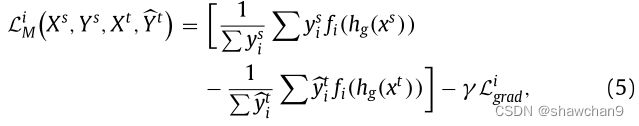
Ys和(戴帽)Yt为one-hot向量，(戴帽)Yt为Xt通过C的softmax输出向量,y d来自域d={s,t}，y d i为y d的第i维的值。L k+1 M对应Ps和Pt 的距离，所以y s k+1和(戴帽)y t k+1被设为1。根据式(4)计算相应分布的Lgrad，γ为超参数。
multi-critic块M的目标是同时最大化所有k + 1损失L i M。

Learning an approximation of the ideal joint hypothesis.

混合分类器C从标记的源样本开始训练,如果C以足够高的置信度(即softmax输出大于给定阈值，例如0.9)对目标示例x t进行分类，则(x t， ~ y t)将被添加训练C。

如果C以较高的置信度对某一类的目标样本进行分类，那么就会出现类偏倚(类似于过拟合)，从而导致模式崩溃。为了克服这样的问题，我们使用了一种简单的正则化技术:在每次迭代中，我们只为每个类添加等量的目标样本。
设hc为c的softmax输出函数。混合分类器C计算k个类的预测，最小化以下交叉熵损失函数：

~ X为源样本集和选中的高置信度目标样本，~ Y为对应的~ X中样本的标签或伪标签。

the combined model

组合目标函数定义为：

当更新θ g和θ c时，梯度惩罚项Lgrad被排除在外。为了简化模型，我们使用单个超参数α，并设置αi = α（i≤k），α k+1 = kα，以强调整体Wasserstein距离相对于类距离的重要性。

Conclusion

本文提出了MCDA方法，在控制理想联合假设合并误差h*的同时，最大限度地减小了源真实风险和域间的离散度。我们的模型使用高可信度的目标样本伪标签和多重Wasserstein距离。