最优传输论文(三) Normalized Wasserstein for Mixture Distributions with Applications in Adversarial Learning

前言

对于混合物分布，已建立的距离度量，如Wasserstein距离，没有考虑到不平衡的混合物比例。因此，即使两个混合物分布具有相同的混合物成分但不同的混合物比例，它们之间的Wasserstein距离也会很大。
在本文中，我们通过引入归一化Wasserstein测度来解决这个问题。其关键思想是引入混合比例作为优化变量，有效地规范化Wasserstein公式中的混合比例。

两个分布PX和PY之间的Wasserstein距离，定义为:

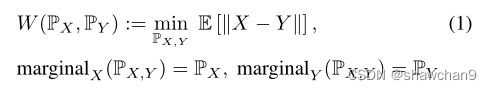
可用W (X, Y)符号来代替W (PX, PY)。

当PX和PY是不同混合比例的混合分布时，由于边际约束，比例不同的混合组分的样品将不得不在PX,Y中耦合在一起(如图1(a))。
本文提出了NW测度来解决多模态分布的不平衡混合比例问题。
设G是一个生成函数数组，其k个分量定义为G:= [G1，… Gk]。设P G,π 是随机变量 X 的混合概率分布，其中X = Gi(Z)，对于概率πi，1≤i≤k，k为混合组分π = [π1，…，πk]T是混合比例的向量。我们假设Z具有正态分布。

引入归一化Wasserstein测度(NW测度)如下:

在这个定义中有两个关键的思想，有助于解决混合分布的模态不平衡问题：
首先，我们没有直接测量PX和PY之间的Wasserstein距离，而是构造了两个中间分布，即PG,π(1)和PG,π(2)。这两个分布具有相同的混合成分(即相同的G)，但可以具有不同的混合比例(即π(1)和π(2)可以不同)。其次，将混合比例π(1)和π(2)作为优化变量。在Wasserstein距离计算之前有效地规范化了混合比例。

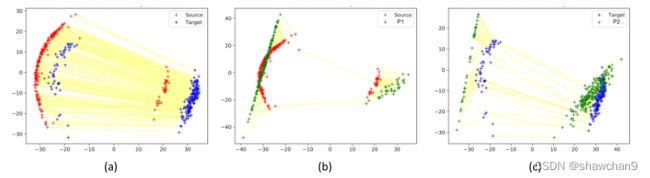
图1.源域(红色表示)和目标域(蓝色表示)有两种模式，模式占比不同。(a)通过估计源和目标分布之间的Wasserstein距离(黄线所示)计算的耦合与来自不同类和遥远模态分量的几个样本相匹配。(b,c)我们提出的归一化Wasserstein测度(3)构建了中间混合物分布P1和P2(绿色所示)，它们分别具有与源和目标分布相似的混合物组分，但具有优化的混合物比例。这显著减少了来自不正确模式的样本之间的耦合数量，并导致与基线相比，区域适应的目标损失减少了42%。

Normalized Wasserstein Measure

G是一个生成器函数数组，定义为G:= [G1，…，Gk] , 其中Gi: Rr(r维)→Rd(d维)。设π是一个含有k个元素的离散概率质量函数，即π = [π1， π2，···，πk]，设Π是所有可能的π集合。
设 PG,π 是一个混合分布，即它是一个随机变量X的概率分布，使X = Gi(Z)。我们假设Z具有正态密度，即Z ~ N (0, I)。我们将G和π分别称为混合成分和比例。
所有这些混合分布的集合定义为:

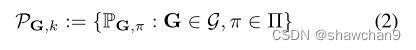
其中k为混合组分的个数，我们感兴趣的是定义一个距离度量，它不受模态比例的差异影响，但对模态成分的位移敏感，即只有当PX和PY的模态成分不同时，距离函数才应该有较高的值。如果PX和PY的模态组分相同，但只是模态比例不同，则距离应该较低。
主要思想是在Wasserstein距离公式(1)中引入混合比例作为优化变量。这就得到了归一化Wasserstein测度(NW测度)，WN (PX, PY)，定义为:

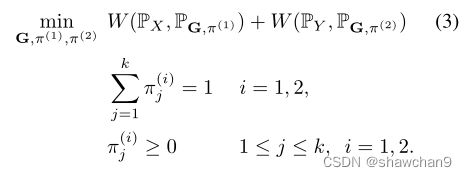
由于归一化Wasserstein优化(3)包含混合物比例π(1)和π(2)作为优化变量，如果两个混合物分布具有相似的混合物组分，但混合物比例不同(即PX = PG,π(1)和PY = PG,π(2))，虽然两者之间的Wasserstein距离可以很大，但二者之间引入的归一化Wasserstein测度将为零。注意，WN是根据一组生成器函数G = [G1，…, Gk]定义的。本文提出的NW测量是一个半距离测量(而不是距离)。
为了计算NW测度，我们使用了类似于Wasserstein距离[1]的对偶计算的交替梯度下降方法。此外，我们使用一个softmax函数施加π约束。
通过估计两个分布之间的Wasserstein距离所产生的耦合如图1-a中的黄线所示。我们观察到，来自不相同混合物组分的样品之间存在许多耦合。另一方面，归一化Wasserstein测度构造了中间的模态归一化分布P1和P2，它们分别耦合到源分布和目标分布的正确模态(见图1中的图(b)和©)。

Theoretical Results

为了使NW测度有效工作，必须适当选择NW公式(式(3))中的模数k。例如，给定两个混合分布，每个混合分布有k个组分，具有2k模数的归一化Wasserstein测度总是0值。我们首先对两个混合分布X和Y做以下假设，我们希望计算它们的NW距离:
A1）如果分布X中的模态 i 和分布Y中的模态 j 属于相同的混合组分，则它们的Wasserstein距离 <= e(此处e为极小值),即 W (PXi, PYj ) < e
A2) 一个混合分布的任意两个模态之间的最小Wasserstein距离至少为δ，即W (PXi, PXj) > δ 和 W (PYi, PYj) > δ ∀i != j，这确保了模式是良好分离的。
A3）我们假设每种模态Xi 和Yi 的比例至少为η，PXi>=η,∀i, PYi ≥ η ∀i。
A4）每个生成器Gi都足够强大，可以捕捉到PX或PY的一种分布模式。

定理1 设PX和PY是两个混合分布，分别满足(A1)-(A4)，有n1和n2个混合组分，其中r个组分重叠。令k* = n1 + n2−r，则k*为最小k，其中 NW(k) 较小 (O(e)) 且 NW(k) − NW(k−1) 相对较大(在O(δη)中)
(A1)-(A3)强制混合分布中的非重叠组分是分离的，重叠组分在Wasserstein距离内是接近的。为了实施(A4)，我们需要防止在g的一个模式中产生多模式,这可以通过使用式(11)中的正则器来满足。

Normalized Wasserstein in Domain Adaptation

在本节中，我们将演示NW方法在无监督域适应(UDA)中对有监督(如分类)和无监督(如去噪)任务的有效性。注意，UDA中的术语unsupervised意味着目标域中的标签信息是未知的，而unsupervised tasks则意味着源域中的标签信息是未知的。
域适应问题的一个常用公式是将Xs和Xt转换为一个特征空间，其中源和目标特征分布之间的距离足够小，可以在空间中为源域计算一个好的分类器。在这种情况下，可以解决以下优化:

其中λ为适应参数，Lcl为经验分类损失函数(例如交叉熵损失)。

当Xs和Xt是混合分布(每个标签对应一个混合组分)具有不同的混合比例时，我们建议使用NW测度作为距离函数。计算NW测度需要训练混合分量G和模态比例π(1)， π(2)。我们利用了源域(即Ys)的标签是已知的这一事实，可以使用这些标签识别源域混合成分，可以避免直接计算G，并使用有条件的源特征分布作为混合组分的代理，如下所示:

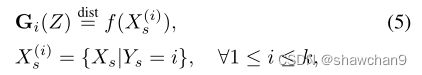
其中dist=表示匹配分布。利用(5)，领域自适应的公式可以写成

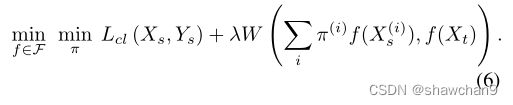
上述公式可以看作是实例加权的一种形式，因为源样本X(i)s的权重是πi。
我们使用神经网络以端到端方式训练模式比例向量π，并在Wasserstein优化中集成实例权重。然而，实例权重用于最大化Wasserstein损失，而我们表明混合比例需要最小化以规范化模式不匹配。

对于无监督任务(源域标签未知)，当源样本的模式分配未知时。在这种情况下，我们使用域适应方法解决以下优化:

其中L unsup(Xs)是源域数据上对应于期望的无监督学习任务的损失。

UDA for unsupervised tasks

对于混合数据集上的无监督任务，我们使用公式(7)进行域自适应。为了实证验证这一公式，我们考虑了图像去噪问题。任务是通过降维对图像进行去噪，即给定目标域图像，我们需要重建与源图像相似的对应干净图像。我们假设数据集中没有(源、目标)对应可用。
当(源、目标)对应不可用时进行去噪，自然的选择是最小化源中的重构损失，同时最小化源与目标嵌入分布之间的距离。我们用NW度量作为距离度量的选择。这将导致以下优化:

其中f(.)是编码器，g(.)是解码器。

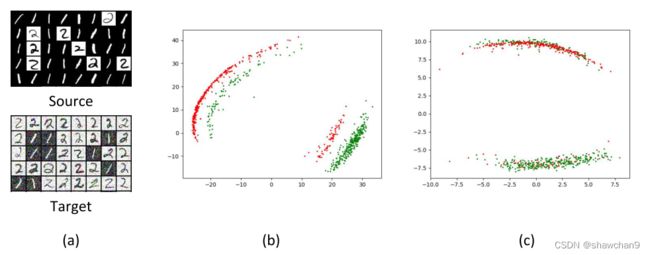
图2。图像去噪的域自适应。(a)源和目标领域的样本。(b)基线模型学习到的源域和目标域嵌入。©通过最小化建议的NW测度学习到的源和目标嵌入。在(b)和©中，红色和绿色点分别表示源样本和目标样本。

作为我们的基线，我们考虑一个只在使用二次重构损失的源域上训练的模型。图2(b)显示了该基线产生的源和目标嵌入。在这种情况下，源嵌入和目标嵌入彼此相距较远。然而，如图2©所示，使用NW公式，源嵌入和目标嵌入的分布非常匹配(估计了模式占比)。

Adversarial Clustering

在本节中，我们使用提出的NW度量来制定一种对抗聚类方法。更具体地说，让输入数据分布有k个底层模式(每个模式代表一个聚类)，我们的方法使用了提出的NWGAN进行聚类，因此显式地处理不平衡组分的数据。
设PX为经验分布。设G和π是NWGAN优化的最优解(9)。对于给定的点xi ~ PX，聚类分配使用到某个模式的最近距离计算，即

为了执行有效的聚类，我们要求每个模式Gj捕获数据分布的一个模式。在不强制任何正则化和广泛使用的生成器函数的情况下，一个模型可以捕获数据分布的多种模式。为了防止这种情况，我们引入了一个正则化项，使不同生成模式之间的加权平均Wasserstein距离最大化。即：

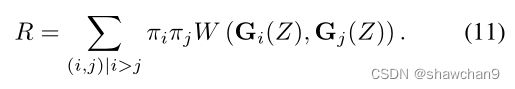
利用这个正则化项，正则化NWGAN的优化目标变为

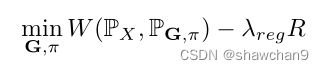
其中λreg为正则化参数。

Normalized Wasserstein GAN

大多数GAN框架可以被视为最小化观测概率分布PX和生成概率分布PY之间距离的方法，其中Y = G(Z)。G被称为生成函数。提出的归一化Wasserstein度量(3)可用于计算生成模型。我们没有像在标准gan中那样估算单个生成器G，而是使用提议的NW度量来估算混合分布PG,π。我们将此GAN称为归一化Wasserstein GAN(或NWGAN)，其公式如下:

所提出的NWGAN生成器是k个模型的混合物，每个模型生成πi大小的生成样本。

Choosing the number of modes

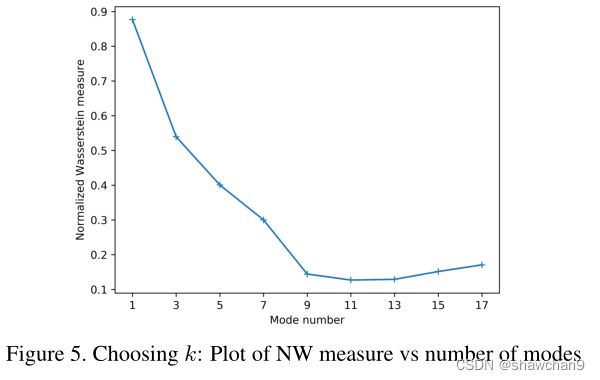
NW(k) is 较小, NW(k − 1) − NW(k) 较大,即当模态组分发生变化时，NW距离差异极大。

Conclusion

由于概率的边缘约束，当应用于不平衡的混合分布时，会导致不期望的结果。
为了解决这个问题，我们提出了归一化Wasserstein。其关键思想是在距离计算中优化混合比例，有效地规范化混合不平衡。我们演示了NW度量在三个机器学习任务中的有用性:GANs，领域适应和对抗聚类。