【机器学习】一文搞懂标准化,归一化,正则化
文章目录
-
- 引言
- 标准化和归一化:
-
- 归一化定义:
- 标准化定义:
- 中心化
- 标准化和归一化的区别与联系,使用场景
-
- 联系
- 区别
- 适用场景:
- 正则化
- 总结:
引言
对于机器学习中的标准化,归一化和正则化的理解,一直都比较模糊,而且在许多技术书籍中,对于它们的使用基本都是一笔带过,不理解概念的话,就不知具体对数据做了哪些操作。因此,在这里专门对这几个概念做学习与总结。
学习之前,先抛出几个问题:
- 这几个概念对数据的具体处理的操作是啥?
- 这些数据的处理适用于哪些场景, 有什么优缺点?
标准化和归一化:
归一化定义:
- 归一化(Normalization): 将一列数据变化到某个固定区间(范围)中, 通常, 这个区间是[0,1],广义的讲, 可以是各种区间, 比如映射到[0,1] 也可以映射到其他范围,在图像中可能会映射到[0, 255], 其他情况也有可能映射到[-1,1];
- 最大值最小值的归一化,范围[0,1]
X i − X m i n X m a x − X m i n \frac{X_i -X_{min}}{X_{max} - X_{min}} Xmax−XminXi−Xmin
- 均值归一化(Mean normalization), 范围[-1,1]
X i − X ‾ X m a x − X m i n \frac{X_i -\overline{X}}{X_{max} - X_{min}} Xmax−XminXi−X
标准化定义:
- 标准化(Standardization): 将数据变换为均值为0,标准差为1的分布。
标 准 化 = X i − μ σ 标准化 = \frac{X_i - \mu}{\sigma} 标准化=σXi−μ
这里需要研究一下公式中的两个数据 μ \mu μ 和 σ \sigma σ 的含义
μ \mu μ : 表示所有样本数据的均值
σ \sigma σ : 表示所有样本数据的标准差
总体标准差:
σ = ∑ i = 1 n ( x i − μ ) 2 n \sigma = \sqrt{ \frac{\sum_{i=1}^n(x_i - \mu)^2}{n} } σ=n∑i=1n(xi−μ)2
样本标准差:
S = ∑ i = 1 n ( x i − x ‾ ) 2 n − 1 S = \sqrt{ \frac{\sum_{i=1}^n(x_i - \overline{x})^2}{n-1} } S=n−1∑i=1n(xi−x)2
- 什么是批标准化(Batch Normalization):
个人理解:批标准化和标准化的不同在于, 计算过程中,批标准化只会选取一小批数据先缩放与平移然后训练参数, 而标准化则会选取所有的数据进行计算。
思考:
一. 标准化之前的数据和标准化之后的数据分别是啥样子的, 通过几个图片来说明?
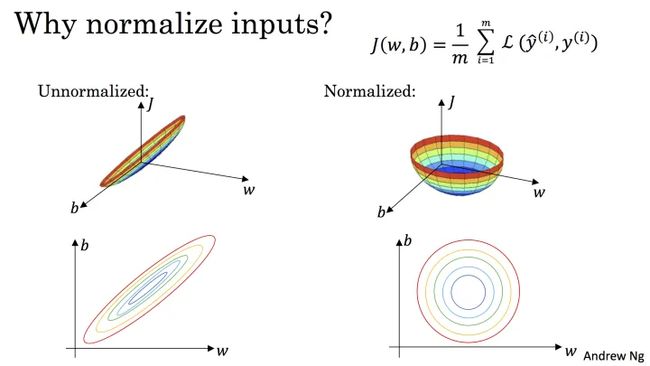
- 下图源于 Andrew Ng 的课程讲义:
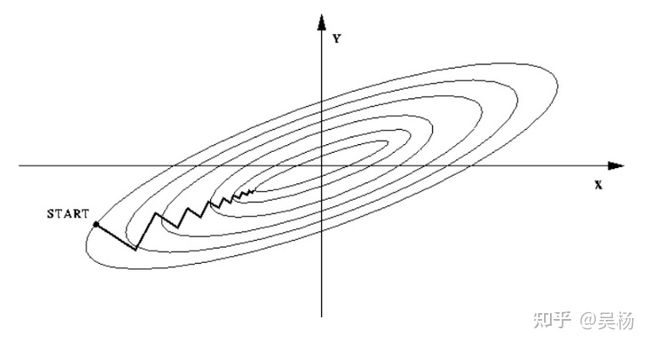
标准化之后, 可以更容易的得出最优参数 w w w和 b b b以及计算出 J ( w , b ) J(w,b) J(w,b)的最小值,从而达到加速收敛的效果。
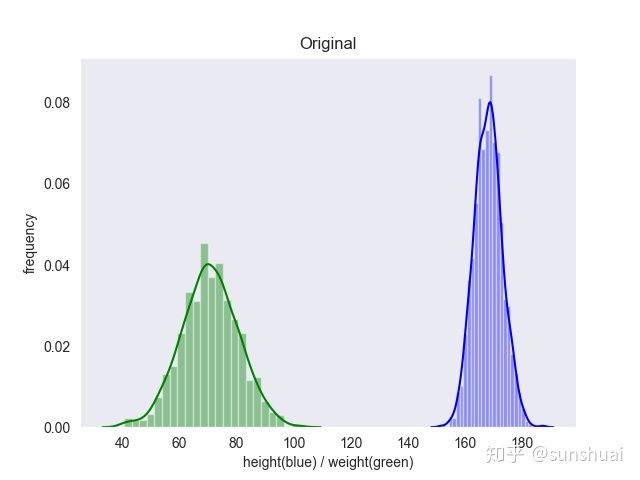
如何数据中有异常点,标准化和归一化之后的数据区别会是什么样子的呢?
参考:
https://www.zhihu.com/question/361290840/answer/939504181
标准化更好保持了样本间距。当样本中有异常点时,归一化有可能将正常的样本“挤”到一起去。比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的,那么,当我们用梯度下降来做分类模型训练时,模型会需要更长的时间收敛,因为将样本分开需要更大的努力!而标准化在这方面就做得很好,至少它不会将样本“挤到一起”。
- 标准化之后,为什么可以做到数据的标准差为1?
标准化之后,数据的均值为0 ,这个可以很明显的看出来,相加一下就得出来了。但是如何证明数据的标准差为1 呢?
标准化公式: a i = x i − μ σ a_i = \frac{x_i - \mu}{\sigma} ai=σxi−μ
其中标准差 σ \sigma σ的公式为:
σ = ∑ i = 1 n ( x i − μ ) 2 n \sigma = \sqrt{ \frac{\sum_{i=1}^n(x_i - \mu)^2}{n} } σ=n∑i=1n(xi−μ)2
推理如下:
假设新数据为 a i a_i ai, 新数据的均值为0,则新数据的标准差可以简化如下:
新 标 准 差 = ∑ i = 1 n ( a i ) 2 n 新标准差 = \sqrt{ \frac{\sum_{i=1}^n(a_i )^2}{n} } 新标准差=n∑i=1n(ai)2
下面只需要证明:
∑ i = 1 n ( a i ) 2 = n \sum_{i=1}^n(a_i )^2 = n ∑i=1n(ai)2=n
其中:
( a i ) 2 = ( x i − μ ) 2 / ( ∑ i = 1 n ( x i − μ ) 2 n ) (a_i)^2 = (x_i - \mu)^2 / (\frac{\sum_{i=1}^n(x_i - \mu)^2}{n}) (ai)2=(xi−μ)2/(n∑i=1n(xi−μ)2)
这种情况下,把 ( a i ) 2 (a_i)^2 (ai)2累加起来, 分母和分子不就抵消了吗,可以得出:
∑ i = 1 n ( a i ) 2 = n \sum_{i=1}^n(a_i )^2 = n ∑i=1n(ai)2=n
因此,成功证明,数据在标准化之后,计算出的标准差为1。
中心化
- 中心化: 也叫做零均值处理, 就是将每个原始数据减去这些数据的均值,本文就不详述了。
标准化和归一化的区别与联系,使用场景
联系
首先说说标准化和归一化的联系:
标准化和归一化其实本质上都是对数据的线性变换,(也就是说,变换前后,数据的形状是一样的,数据的排列顺序没有改变)
我们以标准化为例,说明一下数据是如何平移变换的:
X i − μ σ = X i σ − μ σ \frac{X_i - \mu}{\sigma} = \frac{X_i }{\sigma} - \frac{\mu}{\sigma} σXi−μ=σXi−σμ
当数据给定后,可以认为 μ \mu μ和 σ \sigma σ都是常数, 因此数据就是先缩放 σ \sigma σ,再平移 μ σ \frac{\mu}{\sigma} σμ, 这就是一个线性变换。
区别
- 归一化的数据,会严格限定变换后的范围区间; 而标准化的数据,在变换之后就没有固定的数据范围, 只是均值为0, 标准差为1。
- 归一化的数据缩放比例可能只和极值有关, 而标准化的数据的缩放比例会受到每个数据的影响。
适用场景:
标准化,归一化的用途:
- 机器学习中有一些算法需要使用到距离的计算, 例如PCA, KNN, kmeans等,这种情况下距离的计算容易受到较大的值的影响,因此适合使用标准化,归一化。
- 参数估计的时候会使用梯度下降算法, 在使用梯度下降算法求解最优化问题的时候,使用标准化,归一化的方法可以加快梯度下降的求解速度, 提升模型的收敛速度。
- 如果使用算法不涉及距离相关的, 比如决策树模型,则不需要使用归一化,标准化。
什么时候使用归一化,什么时候使用的正则化:
-
如果对处理后的数据范围有严格要求,使用归一化。
-
如果数据不稳定,存在极端的最大最小值,建议使用正则化。
-
使用距离度量相似性或者使用PCA技术进行降维的时候,建议使用标准化。
-
问题: 均值为0 方差为1 的分布一定是正态分布吗?(自查)
正则化
- 为什么要使用正则化?
正则化是为了防止过拟合,进而增强泛化能力。 之前介绍的标准化,归一化,是作用与训练数据,方便模型训练,提升模型收敛速度的。而正则化是作用于目标函数,减缓参数出现过拟合的现象。
在训练模型的过程中,有许多参数需要通过对损失函数求极小值来确定, 求参数的过程中,希望梯度下降到最小值点, 最终找到合适的w确定模型。
一个原始的,不带正则的线性损失函数如下:
E ( w ) = 1 2 ∑ n = 1 N { t n − w T ϕ ( x n ) } 2 (1) E(\mathbf w) =\frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 \tag{1} E(w)=21n=1∑N{tn−wTϕ(xn)}2(1)
E ( w ) E(\mathbf w) E(w) 是损失函数
t n t_n tn 是测试集合的真实输出,可以看作是训练时候的标签
w \mathbf w w是权重,需要训练得到
ϕ ( ) \phi () ϕ() 是基函数
n 表示测试样本的个数
这个损失函数可以看作是一个平方差的和, 增加的常数因子是为了方便计算
加上正则化的的损失函数如下:
1 2 ∑ n = 1 N { t n − w T ϕ ( x n ) } 2 + λ 2 w T w (2) \frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 + \frac{\lambda}{2} \mathbf w^T \mathbf w \tag{2} 21n=1∑N{tn−wTϕ(xn)}2+2λwTw(2)
从公式中我们可以看出, 我们可以将 λ \lambda λ(也被称之为正则化系数)设置大一些,使得对参数的限制增强。我们加入的正则项,会在训练过程中自动限制参数过大的现象,从而减少过拟合。
1 2 ∑ n = 1 N { t n = w T ϕ ( x n ) } 2 + λ 2 w T w \frac{1}{2}\sum_{n=1}^N\{t_n = \pmb{w}^T \phi(\pmb{x}_n)\}^2 + \frac{\lambda}{2}\pmb{w}^T\pmb{w} 21n=1∑N{tn=wwwTϕ(xxxn)}2+2λwwwTwww
再来介绍一下什么是一次正则,二次正则。
1 2 ∑ n = 1 N { t n − w T ϕ ( x n ) } 2 + λ 2 ∑ j = 1 M ∣ w j ∣ q (3) \frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 + \frac{\lambda}{2} \sum_{j=1}^{M} {\vert w_j \vert}^q \tag{3} 21n=1∑N{tn−wTϕ(xn)}2+2λj=1∑M∣wj∣q(3)
公式里的q就表示模型的阶次,我们可以取 q=1,q=2等等。其中二次正则是比较常用的。这里介绍一下一次正则项的优势: 可以降低维度, 比二次正则更稀疏, 但是, 一次正则有拐点,不是处处可微的,这就给计算带来了难度。
总结:
终于搞懂了标准化,归一化和正则化的区别了。标准化和归一化是作用于训练数据,而正则化是作用与训练参数防止过拟合的。 一般来讲,只要模型涉及距离计算的,都需要使用标准化或者正则化,具体使用哪个方法,可以视模型的实际情况来确定。
参考文档:
https://blog.csdn.net/kdongyi/article/details/83932945
https://zhuanlan.zhihu.com/p/29957294
https://www.zhihu.com/question/20467170/answer/839255695
https://blog.csdn.net/weixin_36604953/article/details/102652160
公式参考:
https://www.cnblogs.com/daizongqi/p/11525397.html