泊松分布一
文章目录
- 1. 泊松分布定义
- 2.泊松分布具体实例
-
- 实例1:
- 实例2:
- 3.生成泊松分布的代码
泊松分布适合于描述单位间隔(时间、距离、面积、体积)内随机事件发生的次数的概率分布。如电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、一年内撞击地球的直径大于1米的陨石数量、CCD/CMOS像元接受光子的数量等等。
1. 泊松分布定义
定义
如果一个离散随机变量 X X X,它的质量密度函数由下式给出,则我们称这个离散随机变量 X X X服从泊松分布
f ( k ; λ ) = p ( X = k ) = λ k e − λ k ! , λ > 0 , k = 0 , 1 , 2 , 3 , . . . f(k;\lambda)=p(X=k)=\frac{\lambda^{k}e^{-\lambda}}{k!},\lambda>0,k=0,1,2,3,... f(k;λ)=p(X=k)=k!λke−λ,λ>0,k=0,1,2,3,...
假设与有效条件
以下假设成立时,泊松分布模型适用:
- 事件在一个时间间隔内发生,且k可以取值0,1,2,…;
- 一个事件的发生不影响下一个事件发生的概率,也就是事件发生是相互独立的;
- 事件发生的平均速率(average event rate)与任何事件的发生无关。一般为简单起见,通常假定事件发生的平均速率为常数,但实际上可能随时间而变化;
- 两个事件不可能在完全相同的时刻发生,即在每一小段的时间内正好有一个事件发生或不发生。
(如果这些条件成立,那么 k k k就是一个泊松随机变量, k k k的分布就是一个泊松分布。)
泊松分布的参数λ是随机事件发生次数的数学期望值,且服从泊松分布的随机变量,其数学期望与方差相等,即 λ = E ( X ) = V a r ( X ) \lambda=E(X)=Var(X) λ=E(X)=Var(X)。
2.泊松分布具体实例
实例1:
在一条特定的河流上,平均每 100 年发生一次洪水。假设发生洪水次数符合泊松分布,那么计算 100 年间发生k = 0、1、2、3、4、5 或 6 次洪水的概率 就可以用泊松分布的公式直接计算。
因为平均事件率(average event rate)是每 100 年发生一次洪水,所以 λ = 1 \lambda=1 λ=1.
p ( 100 年 内 发 生 k 次 洪 水 ) = λ k e − λ k ! = 1 k e − 1 k ! = e − 1 k ! p(100年内发生k次洪水)=\frac{\lambda^{k}e^{-\lambda}}{k!}=\frac{1^{k}e^{-1}}{k!}=\frac{e^{-1}}{k!} p(100年内发生k次洪水)=k!λke−λ=k!1ke−1=k!e−1
p ( 100 年 内 发 生 0 次 洪 水 ) = 1 0 e − 1 0 ! = e − 1 1 ≈ 0.368 p(100年内发生0次洪水)=\frac{1^{0}e^{-1}}{0!}=\frac{e^{-1}}{1}\approx0.368 p(100年内发生0次洪水)=0!10e−1=1e−1≈0.368
p ( 100 年 内 发 生 1 次 洪 水 ) = 1 1 e − 1 1 ! = e − 1 1 ≈ 0.368 p(100年内发生1次洪水)=\frac{1^{1}e^{-1}}{1!}=\frac{e^{-1}}{1}\approx0.368 p(100年内发生1次洪水)=1!11e−1=1e−1≈0.368
p ( 100 年 内 发 生 2 次 洪 水 ) = 1 2 e − 1 2 ! = e − 1 2 ≈ 0.184 p(100年内发生2次洪水)=\frac{1^{2}e^{-1}}{2!}=\frac{e^{-1}}{2}\approx0.184 p(100年内发生2次洪水)=2!12e−1=2e−1≈0.184
p ( k = 3 ) = 0.061 p(k=3)=0.061 p(k=3)=0.061
p ( k = 4 ) = 0.015 p(k=4)=0.015 p(k=4)=0.015
…
实例2:
María Dolores Ugarte及其同事在一篇报道中指出世界杯足球比赛中的平均进球数约为2.5个,也适合泊松分布。 因为平均事件率(average event rate)为每场比赛 2.5 个进球,所以 λ = 2.5。
p ( 一 场 世 界 杯 比 赛 进 k 个 球 ) = 2. 5 k e − 2.5 k ! p(一场世界杯比赛进k个球)=\frac{2.5^{k}e^{-2.5}}{k!} p(一场世界杯比赛进k个球)=k!2.5ke−2.5
p ( 一 场 世 界 杯 比 赛 进 0 个 球 ) = 2. 5 0 e − 2.5 0 ! = e − 2.5 1 ≈ 0.082 p(一场世界杯比赛进0个球)=\frac{2.5^{0}e^{-2.5}}{0!}=\frac{e^{-2.5}}{1}\approx0.082 p(一场世界杯比赛进0个球)=0!2.50e−2.5=1e−2.5≈0.082
p ( 一 场 世 界 杯 比 赛 进 1 个 球 ) = 2. 5 1 e − 2.5 1 ! = 2.5 e − 2.5 1 ≈ 0.205 p(一场世界杯比赛进1个球)=\frac{2.5^{1}e^{-2.5}}{1!}=\frac{2.5e^{-2.5}}{1}\approx0.205 p(一场世界杯比赛进1个球)=1!2.51e−2.5=12.5e−2.5≈0.205
p ( 一 场 世 界 杯 比 赛 进 2 个 球 ) = 2. 5 2 e − 2.5 2 ! = 6.25 e − 2.5 2 ≈ 0.257 p(一场世界杯比赛进2个球)=\frac{2.5^{2}e^{-2.5}}{2!}=\frac{6.25e^{-2.5}}{2}\approx0.257 p(一场世界杯比赛进2个球)=2!2.52e−2.5=26.25e−2.5≈0.257
p ( k = 3 ) = 0.213 p(k=3)=0.213 p(k=3)=0.213
p ( k = 4 ) = 0.133 p(k=4)=0.133 p(k=4)=0.133
p ( k = 5 ) = 0.067 p(k=5)=0.067 p(k=5)=0.067
…
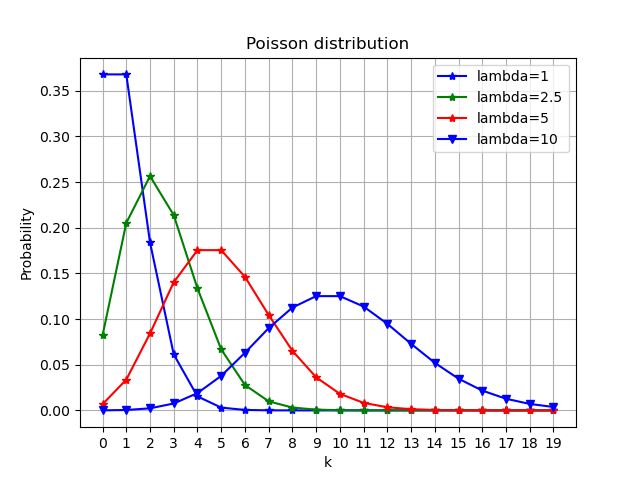
3.生成泊松分布的代码
import numpy as np
import matplotlib.pyplot as plt
def poisson(lam:float,max_k:int):
"""
采用迭代求解的方式计算泊松分布
泊松分布:p(k) = exp(-lam) * (lam**k) / k!,k>=0.
迭代方式:p(k) = p(k-1) * lam / k, k>=1, and p(0) = exp(-lam).
"""
poisson_score = []
# p(0) = exp(-lam)
p_0 = np.exp(-lam)
poisson_score.append(p_0)
k_mult = 1 # 计算阶乘的中间变量
for i in range(1,max_k):
p_k = poisson_score[-1] * lam / i
poisson_score.append(p_k)
return poisson_score
def main():
lam1 = 1
lam2 = 2
lam3 = 5
lam4 = 10
max_k = 20
poisson_score1 = poisson(lam1,max_k)
poisson_score2 = poisson(lam2,max_k)
poisson_score3 = poisson(lam3,max_k)
poisson_score4 = poisson(lam4,max_k)
x = np.arange(len(poisson_score1))
plt.plot(x,poisson_score1,'c*-',c='b',label='lambda='+str(lam1))
plt.plot(x,poisson_score2,'c*-',c='g',label='lambda='+str(lam2))
plt.plot(x,poisson_score3,'c*-',c='r',label='lambda='+str(lam3))
plt.plot(x,poisson_score4,'cv-',c='b',label='lambda='+str(lam4))
plt.title("Poisson distribution")
plt.ylabel("Probability")
plt.xlabel("k")
plt.xticks(x,[str(item) for item in range(len(poisson_score1))]) # 刻度
plt.grid(True)
plt.legend()
plt.show()
if __name__ == "__main__":
main()
参考文献
[1].https://en.wikipedia.org/wiki/Poisson_distribution