手眼标定（传统、SVD、九点） 原理及代码总结

目录

传统手眼标定感性认识：

传统手眼标定原理图：

        Eye in hand

        Eye to hand

传统手眼标定教学视频：

传统手眼标定代码：

SVD手眼标定法原理：

SVD求解数学原理：

SVD手眼标定法代码：

九点标定法感性认识：

九点标定法代码：

九点标定法流程：

总结：

---

传统手眼标定感性认识：

        相机标定（一）：机器人手眼标定 - 知乎

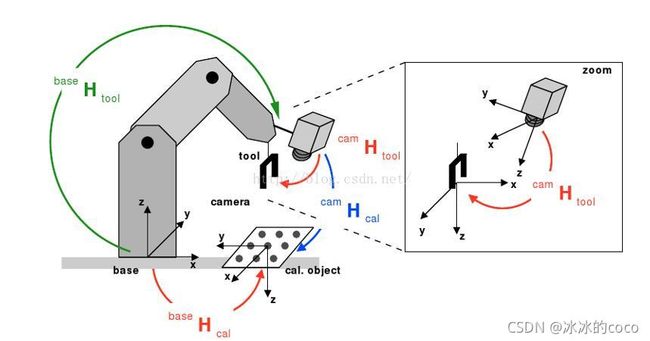
传统手眼标定原理图：

        Eye in hand

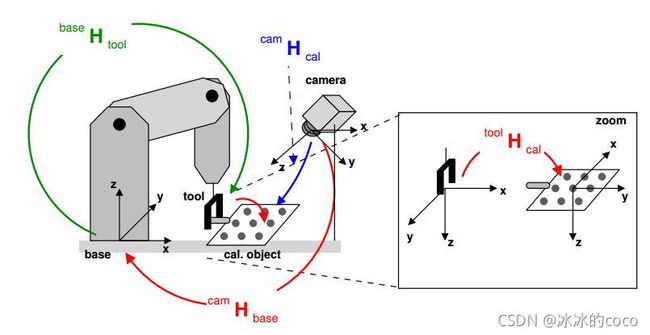
        Eye to hand

        

传统手眼标定教学视频：

        手眼标定—原理与实战（上篇）_哔哩哔哩_bilibili

        手眼标定原理与实战(下篇)_哔哩哔哩_bilibili

传统手眼标定代码：

        利用 `calibrateHandeye()` 函数

        OpenCV手眼标定（calibrateHandeye()）_hello-CSDN博客_opencv手眼标定

SVD手眼标定法原理：

         相机标定(三)——手眼标定_偷得浮生半日闲-CSDN博客_相机手眼标定

SVD求解数学原理：

        ​​​​​​SVD分解（奇异值分解）求旋转矩阵_Bryan_Zhang的专栏-CSDN博客_svd求解旋转平移矩阵

SVD手眼标定法代码：

#SVD分解手眼标定法 
def rigidTransform3d(A, B):
        #整理传入数据形状
        A = np.mat(np.array(A).reshape(9, 3))
        B = np.mat(np.array(B).reshape(9, 3))
        
        assert len(A) == len(B)
        N = A.shape[0]
        #对十个数据取平均值
        mu_A = np.mean(A, axis=0)  
        mu_B = np.mean(B, axis=0)
        #对数据减去均值（中心点）
        AA = A - np.tile(mu_A, (N, 1))  
        BB = B - np.tile(mu_B, (N, 1))
        #计算矩阵H
        H = np.transpose(AA) * BB  # H = A.T * B
        #SVD分解
        U, S, Vt = np.linalg.svd(H)  
        #计算旋转矩阵
        rotationMatrix = Vt.T * U.T  # R =  V * U.T
        #反射矩阵检测
        if np.linalg.det(self.__rotationMatrix) < 0:
            print("Reflection detected")
            Vt[2, :] *= -1
            rotationMatrix = Vt.T * U.T
        #计算平移矩阵
        translationMatrix = -rotationMatrix * mu_A.T + mu_B.T
            
        return rotationMatrix, translationMatrix

        

 

九点标定法感性认识：

        手眼标定（九点法）_黄昏的晨曦-CSDN博客_手眼标定

    理解什么是仿射变换：

                刚体变换和仿射变换的区别_w_weixiaotao的博客-CSDN博客_刚体变换和仿射变换

九点标定法代码：

#利用像素坐标和机械手坐标（至少三个点）得到仿射矩阵，完成像素坐标到机械手坐标的转换
#origin_points_set 标定板像素坐标点集
#target_points_set 机械手抓取坐标点集
import cv2
cv2.estimateAffine2D(origin_points_set, target_points_set)

九点标定法流程：

        Eye in hand方案  、九点标定法 

        首先，将机械手移到标定板正上方

        然后，通过相机得到九个检测点在相机坐标系下的坐标p_camera

        最后，让机械手末端依次触碰九个检测点，得到检测点在机械手坐标系下的坐标p_base

        将得到的九组点分别做成A, B列表，传入函数就可以得到R,T矩阵啦

总结：

        九点标定法只能识别x，y坐标，属于2D平面标定，在标定过程中z是未知的（需要自己确定）

        如果需要实现3D抓取，需要进行传统手眼标定（棋盘格标定）或者SVD手眼标定法

        SVD手眼标定法可以实现3D标定，但是在标定的时候要知道深度信息（z是已知的）

       

        实际使用中发现九点标定法最准确

        SVD和传统方法会存在一定精度问题，一般作为迭代法的初始解提高精度