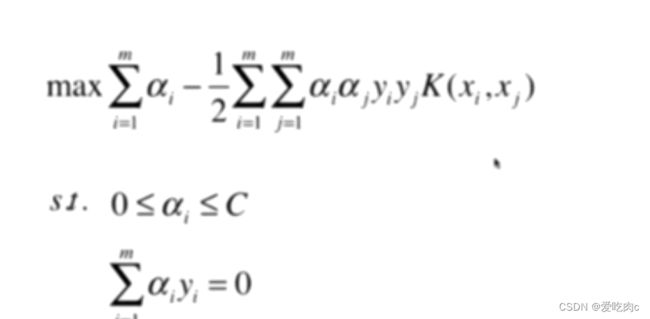核函数（多项式，高斯核）以及svm解决回归问题

---

一、SVM最优化问题转换

变换为数学上一个更好解的

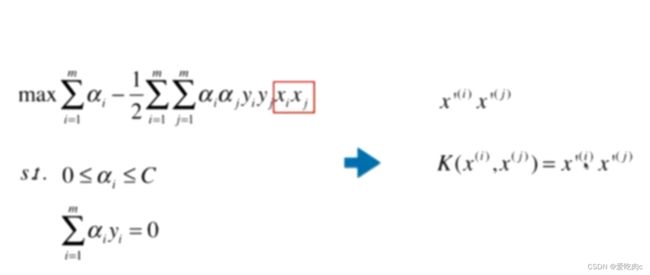
在这个式子中有重要的一项Xi，Xj 两个样本的点乘，分别都是一个向量对于多项式，
我们通常是将Xi变为X‘i Xj同理，但是这样会加大计算复杂度.
也会浪费空间，因为我们需要把X’i保存起来
但是对于核函数，我们往往只需要XI和Xj即可，通过一个核函数达到同样的效果

	注：核函数不只是SVM特有的，只要式子中有Xi，Xj就可以考虑核函数

1、多项式核函数

在这里，为了表示方便，我们先使用二项式核函数.
一般的多项式核函数，我们都会先把Xi–>X‘i，之后再将转换之后的进行点乘，但是对于核函数我们只要将Xi和Xj通过一个核函数即可。

二、高斯核函数

1.引入库

高斯核函数又被称为径向基函数

---

	将每一个样本点映射到一个无穷维的样本点空间，后续通过例子就可以明白

1、多项式特征

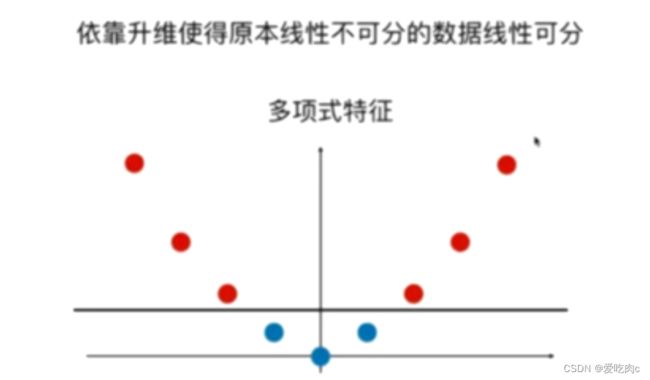
多项式特征将线性不可分变为线性可分
这里采用简单的一维变二维

如图，我们发现，这个一维线性不可分，因此我们增加一维，x²，就可变为线性可分了。

---

2、高斯核函数升维举例

在这里我们将y取了两个数据点L1,L2 也成为land mark 地标
此时每一个x都由图中的表达式变成一个二维数据

import numpy as np
import matplotlib.pyplot as plt

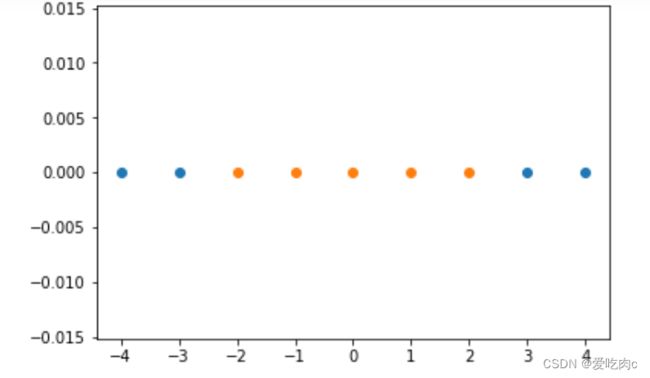
x=np.arange(-4,5,1)
y=np.array((x>=-2)&(x<=2),dtype='int')
plt.scatter(x[y==0],[0]*len(x[y==0]))
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

def guassion(x,l):
    gamma=1.0#为了简单，这里gamma取1.0
    return np.exp(-gamma*(x-l)**2) #在这里因为x和l都为一维的 所以直接加括号平方即可l1,l2=-1,1
x_new=np.empty((len(x),2))
#返回i是索引，data是数据
for i,data in enumerate(x):
    x_new[i,0]=guassion(data,l1)
    x_new[i,1]=guassion(data,l2)
plt.scatter(x_new[y==0,0],x_new[y==0,1])
plt.scatter(x_new[y==1,0],x_new[y==1,1])
plt.show()

		一维变为2维之后就变得线性可分了

高斯核：每一个数据点都是一个地标，有多少地标就有多少维
例如，把其中一个样本当作一个地标，其余点包括该点利用高斯核公式便可得到一个值
该值就是每个点m维中的对应的一个元素

mn的数据便会映射成mm维，这也就可以理解之前的一句话
将一个数据映射到一个无穷维，因为一个样本往往有很多数据
但是这也会增加计算开销，但是高斯核函数在自然语言领域有很好的应用
因为自然语言领域的维度很高。

3、高斯核函数超参数gamma

与高斯函数类似，但又不同
高斯核函数是gamma越大，高斯分布越集中，越窄，反之越宽。
举例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#添加噪声
x,y=datasets.make_moons(noise=0.15,random_state=666)
plt.scatter(x[y==0,0],x[y==0,1],color='r')
plt.scatter(x[y==1,0],x[y==1,1],color='b')
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
def rbfkernelsvc(gamma=1.0):
    return Pipeline([
        ("std",StandardScaler()),
        ("svc",SVC(kernel="rbf",gamma=gamma))
    ])
rbf=rbfkernelsvc(gamma=1.0)
rbf.fit(x,y)
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0]))*100).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2]))*100).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)
    zz=y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_camp=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0,x1,zz,linewidth=5,camp=custom_camp)
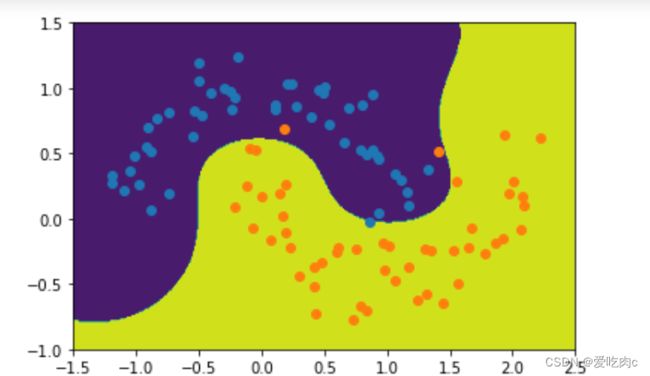
plot_decision_boundary(rbf,[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()

gamma=100，过拟合

rbf100=rbfkernelsvc(gamma=100)
rbf100.fit(x,y)
plot_decision_boundary(rbf100,[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()   #过拟合，泛化能力不好

gamma=0.1，欠拟合

rbf01=rbfkernelsvc(gamma=0.1)
rbf01.fit(x,y)
plot_decision_boundary(rbf01,[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()  #欠拟合

对于不同的问题，我们要选取最合适的不同的gamma

三、svm解决回归问题

与分类问题不同，回归问题也有margin但是，对于回归问题，
我们是希望margin中的数据点越多越好，更好的拟合
简单举例

boston=datasets.load_boston()
x=boston.data
y=boston.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.svm import SVR,LinearSVR
def standscalersvr(epsilon=0.1):
    return Pipeline([
        ("std",StandardScaler()),
        ("linearsvr",LinearSVR(epsilon=epsilon))
    ])
linearsvr=standscalersvr()
linearsvr.fit(x_train,y_train)
linearsvr.score(x_test,y_test)

当然我们也可以使用svr，这就有许多超参数
如果kenerl=poly 就要考虑degree和c
kernel=rbf，就要考虑gamma等
这里不在一一叙述

总结

之前，除了knn是非参数学习，其他都是参数学习
下一章我们学习一个重要的非参数学习----决策树